Методы определения внутренних усилий и построения их эпюр для многопролетных балок

В сечениях многопролетных балок, загруженных поперечными нагрузками, возникают две составляющие внутренних усилий: поперечные силы и изгибающие моменты. Поперечные силы являются равнодействующими касательных сил, распределенных по площади сечения. Они направлены вдоль главной вертикальной оси инерции поперечного сечения. Изгибающие моменты являются равнодействующими моментов нормальных сил относительно оси, направленной перпендикулярно к грузовой плоскости. Напомним правило знаков внутренних усилий в произвольном сечении балки.

Поперечная сила имеет знак + (плюс), если она вызвана силами, направленными вверх слева от сечения, или силами, направленными вниз справа от сечения.

Изгибающий момент имеет знак + (плюс), если он вызван силами направленными вверх независимо от их расположения по отношению к сечению, или моментами, направленными слева от сечения по ходу часовой стрелки, или справа от сечения против хода часовой стрелки.

Усилия принимаются со знаком минус, если нагрузки направлены противоположно.

На рис.2,9 показаны направления нагрузок, при которых в заданном сечении возникают усилия со знаком плюс или минус.

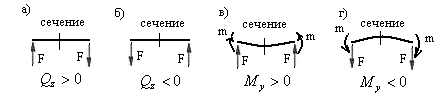
Рис.2.9

Определение внутренних усилий и построение их эпюр для многопролетных балок может быть выполнено методом сечений или методом площадей.

Напомним последовательность построения эпюр указанными методами.

При использовании метода сечений необходимо:

- определить реакции опор заданной балки методом равновесия дисков или методом неполного освобождения связей;

- каждый диск или всю балку разбить на участки, ограниченные точками приложения сосредоточенных сил и моментов, а также границами распределенных нагрузок;

- в пределах каждого участка наметить произвольное сечение на переменном расстоянии x_i от начала координат и составить уравнения поперечных сил и изгибающих моментов для каждого участка. В зависимости от характера загружения балки эти уравнения могут быть линейными, квадратичными, или третьей степени относительно переменной x_i;

- вычислить необходимое число ординат внутренних усилий и построить их эпюры, т.е. графики изменения поперечных сил и изгибающих моментов по длине балки.

Примечание: если реакции опор балки определяются методом равновесия дисков, используя поэтажную схему заданной балки, то построение эпюр методом сечений целесообразно осуществлять последовательно для каждого диска в одинаковом масштабе, а затем объединить их вдоль оси заданной балки. Если же реакции опор определяются по методу неполного освобождения связей, то построение эпюр осуществляется для всей балки.

При использовании метода площадей построение эпюр поперечных сил и изгибающих моментов осуществляется для всей балки сразу, независимо от метода определения реакций опор. Для этого заданную балку делят на участки и их границы нумеруют слева на право цифрами 0,1,2,3…n. Интервалы загружения балки распределенными нагрузками следует разделить на несколько участков, имеющих равные длины.

Используя известные правила и формулы метода площадей, вычисляют поперечные силы в начале и в конце каждого участка и строят эпюру Q_z. Затем вычисляют изгибающие моменты и строят эпюру M_y.

Напомним правила и формулы метода площадей.

Поперечная сила и изгибающий момент в начале крайнего левого участка всегда известны по условиям закрепления и загружения балки. Они равняются соответственно сосредоточенной силе и сосредоточенному моменту в этом сечении с соответствующими знаками.

Поперечная сила в конечном сечении произвольного участка равняется алгебраической сумме поперечной силы в начальном сечении этого участка и площади распределенной нагрузки в пределах этого участка.

Или: 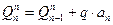(2.7)

Произведение q·a_n равняется площади распределенной нагрузки в пределах участка.

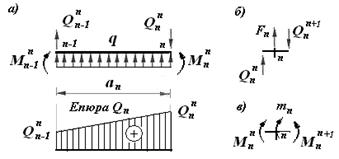
Рис.2.10

Распределенная нагрузка принимается со знаком плюс, если действует вверх и со знаком минус, если действует вниз. На рис.2.10 показаны направления нагрузок и усилий, имеющих знак плюс.

Поперечная сила в начальном сечении любого последующего участка равняется алгебраической сумме поперечной силы в конечном сечении предыдущего участка и сосредоточенной силы Fn, которая действует на границе этих участков.

Или: 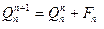(2.8)

Если на границе двух участков отсутствует сосредоточенная сила, то поперечные силы в конечном сечении предыдущего участка и в начальном сечении последующего участка имеет одинаковое значение, то есть .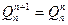

Изгибающий момент в конечном сечении произвольного участка равняется алгебраической сумме изгибающего момента в начальном сечении этого участка и площади эпюры поперечных сил в пределах этого участка.

Или: 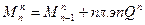(2.9)

Изгибающий момент в начальном сечении любого последующего участка равняется алгебраической сумме изгибающего момента в конечном сечении предыдущего участка, и сосредоточенного момента, который действует на границе этих участков.

Или: 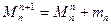(2.10)

Если на границе двух участков отсутствует внешний сосредоточенный момент, то изгибающие моменты в конечном сечении предыдущего участка и в начальном сечении последующего участка имеет одинаковое значение, то есть .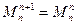

Пример 2.1. Последовательность построения эпюр поперечных сил и изгибающих моментов методом площадей проследим на примере балки, размеры и нагрузки которой показаны на рис.2.7,а.

Последовательность решения задачи:

1) Определяем опорные реакции заданной балки, используя метод равновесия дисков (см. рис.2.7,б и определение реакций из уравнений, составленных в §2.2);

2) Вычерчиваем заданную балку без опор и загружаем её внешними нагрузками и вычисленными из уравнений равновесия реакциями опор (рис.2.11,а);

3) Делим балку на участки и обозначаем их границы цифрами 0,1,2…(рис.2.11,б);

4) Вычисляем поперечные силы в начале и в конце каждого участка, используя приведенные выше правила 1,2,3, и строим эпюру поперечных сил (рис.2.11,в);

5) Вычисляем изгибающие моменты в начале и в конце каждого участка, используя правила 1,4,5, и строим эпюру изгибающих моментов (рис.2.11г).

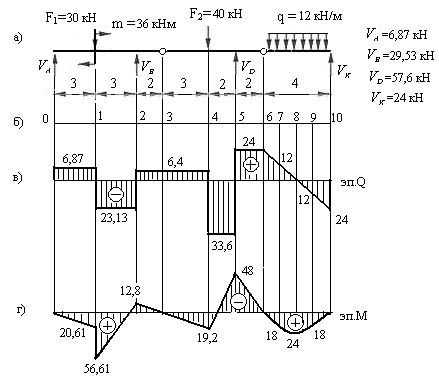
Рис.2.11

Предлагаем проверить величины ординат эпюр поперечных сил и изгибающих моментов, используя правила метода площадей и убедиться в том, что они вычислены правильно.

Вопросы для самоконтроля полученных знаний.

1. Что представляет собой многопролетная статически определимая балка?

2. Каковы особенности работы многопролетной статически определимой балки в сравнении с неразрезной балкой?

3. Как можно определить число шарниров в многопролетной статически определимой балке?

4. Приведите два основных варианта расстановки шарниров в многопролетной балке.

5. Каким требованиям с точки зрения геометрической неизменяемости должно удовлетворять расположение шарниров?

6. Какие типы элементов различают в многопролетной статически определимой балке?

7. Что такое этажная схема?

8. По какому признаку устанавливают взаимное расположение смежных элементов на этажной схеме?

9. Каков порядок расчета многопролетной балки на неподвижную нагрузку?