Аналитические методы определения реакций опор многопролетных балок
Для определения реакций, возникающих в опорах загруженной многопролетной балки, используют два метода:
- метод равновесия дисков;
- метод неполного освобождения связей.
При определении опорных реакций методом равновесия дисков освобождают все связи заданной балки (опорные связи и шарниры, объединяющие диски). В результате получаем D изолированных дисков. Каждый диск загружаем заданными нагрузками и неизвестными реакциями удаленных связей. Цилиндрический шарнир передает от одного диска к другому вертикальные и горизонтальные составляющие реакции. Эти составляющие равны по величине и противоположно направлены. В защемляющей опоре возникают три составляющие реакции (опорный момент, вертикальная и горизонтальная силы), в шарнирно неподвижной опоре возникают вертикальная и горизонтальная составляющие реакции, в шарнирно подвижной опоре возникает только вертикальная реакция.
Таким образом, общее число неизвестных реактивных сил, подлежащих определению, будет равно сумме:
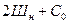 ,
,
где Шн – число цилиндрических шарниров, а
Со - число простых опорных связей балки.
Для определения этих неизвестных составляем 3D уравнений равновесия (по 3 уравнения равновесия для каждого диска). Эти уравнения можно составлять, рассматривая диски в произвольном порядке.
Если число уравнений равновесия равно числу неизвестных сил сопротивления, возникающих в освобожденных связях балки, т.е., если соблюдается равенство:
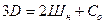 , то рассматриваемая балка статически определима и все неизвестные определяются из решения системы уравнений равновесия. Если число уравнений окажется больше числа неизвестных, то заданная балка геометрически изменяемая или подвижна, а если число уравнений меньше числа неизвестных, балка имеет лишние связи и является статически неопределимой.
, то рассматриваемая балка статически определима и все неизвестные определяются из решения системы уравнений равновесия. Если число уравнений окажется больше числа неизвестных, то заданная балка геометрически изменяемая или подвижна, а если число уравнений меньше числа неизвестных, балка имеет лишние связи и является статически неопределимой.
Примечание. При загружении балки только вертикальными и моментными нагрузками, в шарнирах, а также в неподвижных опорах горизонтальные составляющие реакций равны нулю. В этом случае для каждого диска составляют по два уравнения равновесия, используя рациональные условия.
Таким образом, по методу равновесия дисков определяются одновременно опорные реакции и реакции шарниров.
Рассмотрим пример определения реакций опор и шарниров для балки, представленной на рис.2.7,а.
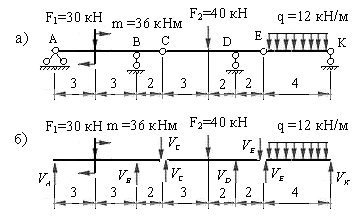
Рис.2.7
Нагрузки и размеры балки в метрах показаны на расчетной схеме балки.
Заданная балка состоит из трех дисков (АС, СЕ и ЕК), объединенных между собой шарнирами С и Е. Опора А шарнирно неподвижная, а опоры В, D и К – шарнирно подвижные в направлении оси балки.
Освободим балку от всех опор и шарниров. В результате получим три изолированных диска (рис.2.7,б). Загружаем каждый диск заданными нагрузками и реакциями удаленных связей. В опорах возникают только вертикальные реакции, которые направляем вверх. Реакции шарниров С и Е действуют на два объединяемых диска. Они равны по величине и направлены вертикально в противоположные стороны. Напомним, что при отсутствии горизонтальных или наклоненных к оси балки нагрузок, горизонтальные реакции шарниров равны нулю. Составляем по два уравнения равновесия для каждого диска, используя условия равенства нулю суммы моментов всех сил приложенных к отдельным дискам относительно двух произвольных точек.
Диск АС.
Условия равновесия: 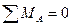 ,
, 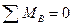
Уравнения равновесия:
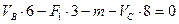 , или
, или 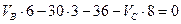 (2.1)
(2.1)
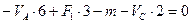 ,или
,или 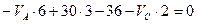 (2.2)
(2.2)
Диск СЕ.
Условия равновесия: 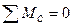 ,
, 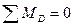
Уравнения равновесия:
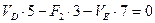 , или
, или 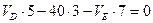 (2.3)
(2.3)
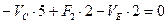 ,или
,или 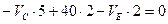 (2.4)
(2.4)
Диск ЕК.
Условия равновесия: 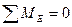 ,
, 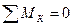
Уравнения равновесия:
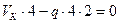 , или
, или 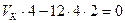 (2.5)
(2.5)
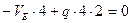 ,или
,или 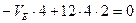 (2.6)
(2.6)
Уравнения (2.1)-(2.4) содержат по 2 неизвестные реакции, уравнения (2.5) и (2.6) по одной неизвестной. Из этих уравнений находим: 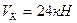 и
и 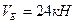
Подставляем значение 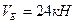 в уравнения (2.3) и (2.4) и находим из их решения
в уравнения (2.3) и (2.4) и находим из их решения 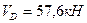 и
и 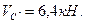
Подставляем значение 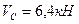 в уравнения (2.1) и (2.2) и находим из их решения
в уравнения (2.1) и (2.2) и находим из их решения 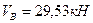 и
и 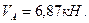
Для проверки правильности решения уравнений равновесия используем условие равенства нулю суммы проекций всех сил, приложенных к балке на вертикальную ось. Эту проверку выполняют для балки в целом. При этом реакции шарниров не учитывают, так как они самоуравновешиваются.

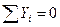

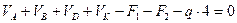 ,
,
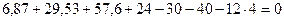

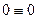
При использовании поэтажной схемы многопролетной балки определение реакций связей упрощается, так как она позволяет установить рациональный порядок рассмотрения дисков и составления уравнений равновесия. Например, для рассмотренной выше балки, поэтажная схема которой представлена на рис.2.4, сначала составляют уравнения равновесия подвесного диска ЕК (смотрите уравнения (2.5) и (2.6)). Из этих уравнений определяют реакции 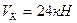 и
и 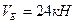 . Затем составляют уравнения равновесия передаточного диска СЕ (уравнения (2.3) и (2.4)), из этих уравнений определяют реакции
. Затем составляют уравнения равновесия передаточного диска СЕ (уравнения (2.3) и (2.4)), из этих уравнений определяют реакции 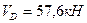 и
и 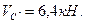 Последним рассматривают равновесие главного диска АС, составляют и решают уравнения (2.1) и (2.2). Получают величины реакций
Последним рассматривают равновесие главного диска АС, составляют и решают уравнения (2.1) и (2.2). Получают величины реакций 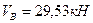 и
и 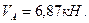
Рассмотрим определение реакций опорных связей методом неполного освобождения связей. При использовании этого метода освобождают только опорные связи заданной балки. В результате получают геометрически изменяемую систему дисков, объединенных между собой шарнирами. Степень её геометрической изменяемости равна числу шарниров балки. Затем загружают балку заданными нагрузками и неизвестными реакциями удаленных опор. Для такой геометрически изменяемой системы необходимо составить три уравнения равновесия в целом (или два уравнения, если нагрузки перпендикулярны к оси балки) и дополнительные уравнения равновесия отдельных частей балки относительно шарниров, объединяющих эти части. Нетрудно заметить, что условия равновесия отдельных частей относительно шарниров, эквивалентны условиям равенства нулю изгибающих моментов в шарнирах балки. Число дополнительных уравнений всегда равно числу шарниров балки. Таким образом, по методу неполного освобождения связей реакции шарниров не определяются, а, следовательно, число неизвестных реакций меньше чем по методу равновесия дисков.
Но уравнения для их определения более сложные, чем в методе равновесия дисков, особенно при большом числе дисков балки. Поэтому метод неполного освобождения связей не рекомендуется применять, если балка имеет более трех дисков.
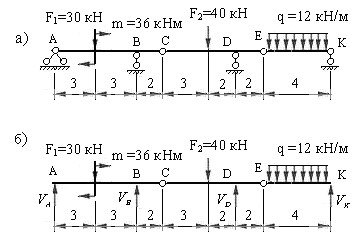
Рис.2.8
Определим реакции опор балки, рассмотренной выше (рис.2.8,а), методом неполного освобождения связей.
Освободим опорные связи заданной балки, а их действие на балку компенсируем приложением вертикальных реакций (рис.2.8,б). Напомним, что при вертикальных нагрузках, горизонтальная реакция неподвижной опоры А не возникает. Для определения четырех неизвестных реакций составляем два уравнения равновесия балки в целом, используя условия: 1) 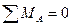 , 2)
, 2) 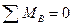 и два дополнительных уравнения, используя условия равенства нулю изгибающих моментов в шарнирах С и Е балки: 3)
и два дополнительных уравнения, используя условия равенства нулю изгибающих моментов в шарнирах С и Е балки: 3) 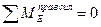 , 4)
, 4) 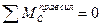 .
.
Составляем четыре уравнения, используя приведенные условия:
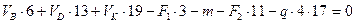 (а)
(а)
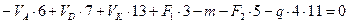 (б)
(б)
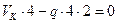 (в)
(в)
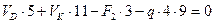 (г)
(г)
Выбираем рациональный порядок решения составленных уравнений:
Из уравнения (в) определяем 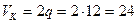 кН.
кН.
Из уравнения (г) определяем
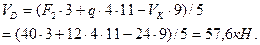
Затем из уравнений (а) и (б) определяем 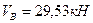 и
и 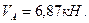
Для проверки вычисленных реакций используем условие: 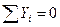

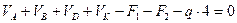 ,
,
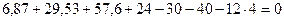

Дата добавления: 2019-04-03; просмотров: 2506;
