Стержневая система называется неподвижной, если её точки не имеют абсолютных смещений в пространстве или на плоскости.
Следует иметь в виду, что только неподвижные и геометрически неизменяемые стержневые системы могут воспринимать и удерживать в устойчивом равновесии внешние нагрузки.
Существуют два метода исследования геометрической неизменяемости и неподвижности стержневых систем: кинематический и статический.
Кинематический метод исследованиясостоит в определении общего числа степеней свободы стержневой системы. Если стержневая система без опорных связей имеет в пространстве 6 степеней свободы, а на плоскости – 3, то она является геометрически неизменяемой. Если стержневая система с опорными связями не имеет степеней свободы, то она является неподвижной.
Используя приведенные определения и формулы (1.2)-(1.5) получаем следующие кинематические условия геометрической неизменяемости и неподвижности систем:
а) Условия геометрической неизменяемости пространственных и плоских систем, образованных по первому варианту:
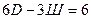 (1.6)
(1.6)
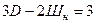 (1.7)
(1.7)
б) Условия геометрической неизменяемости пространственных и плоских систем, образованных по второму варианту:
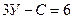 (1.8)
(1.8)
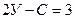 (1.9)
(1.9)
в) Условия неподвижности пространственных и плоских систем, образованных по первому варианту:
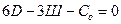 (1.10)
(1.10)
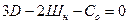 (1.11)
(1.11)
г) Условия неподвижности пространственных и плоских систем, образованных по второму варианту:
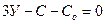 (1.12)
(1.12)
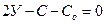 (1.13)
(1.13)
Если при исследовании стержневых систем условия (1.6) – (1.13) выполняются, т.е. левые их части равны правым, то стержневая система является геометрически неизменяемой или неподвижной.
Если же левые части этих условий окажутся большими чем правые, то исследуемая система геометрически изменяема либо подвижна.
Если же левые части этих условий окажутся меньшими чем правые, то исследуемая система имеет лишние связи, т.е. является статически неопределимой.
Следует иметь в виду, что условия (1.6) – (1.13) являются необходимыми, но недостаточными условиями геометрической неизменяемости и неподвижности стержневых систем, так как они не учитывают качественного расположения связей систем. Поэтому кинематический метод необходимо использовать совместно со структурным анализом образования стержневых систем. Структурный анализ базируется на следующих правилах:
1) Два диска на плоскости, объединенные между собой тремя шарнирно стержневыми связями, образуют геометрически неизменяемую систему, если они не параллельные и не пересекаются в одной точке. На рис.1.13,а показано правильное расположение связей в системе двух дисков, а на рис.1.13,б и рис.1.13,в – не правильное их расположение. В первом случае система геометрически неизменяемая, а в двух других случаях она геометрически изменяемая.
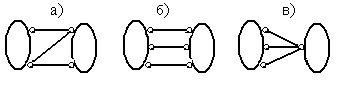
Рис.1.13
2) Шарнирный треугольник является геометрически неизменяемой системой, а шарнирный четырехугольник – геометрически изменяемой. Поэтому всякая сложная система, составленная из шарнирных треугольников, является геометрически неизменяемой, а система, содержащая шарнирный четырехугольник, является геометрически изменяемой. На рис.1.14,а показан пример геометрически неизменяемой системы, а на рис.1.14,б пример геометрически изменяемой системы.
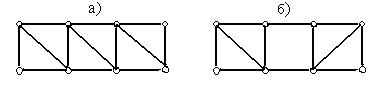
Рис.1.14
3) Сплошной или решетчатый диск на плоскости, закрепленный с помощью трех опорных связей является неподвижным, если указанные связи не параллельны между собой и не пересекаются в одной точке. На рис.1.15,а показана неподвижная система, а на рис.1.15,б и 1.15,в) – подвижные системы.
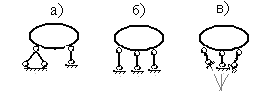
Рис.1.15
Статический метод исследованиягеометрической неизменяемости и неподвижности стержневых систем состоит в определении реактивных сил сопротивления, возникающих в связях от любых нагрузок. Если эти силы сопротивления имеют единственные определенные и конечные значения, то исследуемая стержневая система геометрически неизменяемая или неподвижна. Если же указанные силы сопротивления принимают неопределенные или бесконечные значения, то исследуемая система геометрически изменяемая или подвижна.
При исследовании стержневой системы статическим методом не всегда следует определять реакции связей. Если из условий равновесия составлена система уравнений и определитель этой системы не равен нулю, то такая система является геометрически неизменяемой или неподвижной.
На рис.1.16 показано тело, шарнирно закрепленное двумя стержнями и загруженное вертикальной силой. От действия этой силы в стержнях возникнут продольные усилия 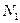 и
и 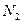 .
.
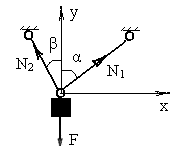
Рис.1.16
Для определения этих усилий составляем два уравнения из условий равновесия загруженного тела:
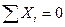 и
и 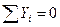
Получаем систему уравнений равновесия:
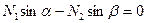
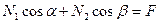
Составим определитель этой системы, раскроем его и установим, в каких случая он может быть равным нулю (только в этих случаях усилия могут принимать неопределенные либо бесконечные значения).
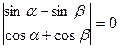 , откуда
, откуда 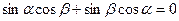
Или 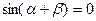 . Это равенство возможно в двух случаях: 1) когда
. Это равенство возможно в двух случаях: 1) когда 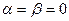 , т.е. когда стержни совмещаются и образуют мгновенно изменяемую систему; 2) когда
, т.е. когда стержни совмещаются и образуют мгновенно изменяемую систему; 2) когда 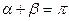 , т.е. когда стержни располагаются на одной горизонтальной или наклонной прямой и также образуют мгновенно изменяемую систему. Во всех иных случаях рассматриваемая стержневая система неподвижна и способна удерживать заданную нагрузку.
, т.е. когда стержни располагаются на одной горизонтальной или наклонной прямой и также образуют мгновенно изменяемую систему. Во всех иных случаях рассматриваемая стержневая система неподвижна и способна удерживать заданную нагрузку.
Следует иметь в виду, что статический метод всегда позволяет получить точный ответ на вопрос является ли исследуемая система геометрически неизменяемой или неподвижной, либо относится к другой категории.
Дата добавления: 2019-04-03; просмотров: 839;
