Число независимых параметров, определяющих положение элемента стержневой системы или системы в целом, составляет степень их свободы.
Ранее отмечалось, что пространственный диск имеет 6 степеней свободы, а плоский диск имеет три степени свободы.
Стержневые системы, образованные по первому варианту состоят из нескольких дисков, объединенных между собой шарнирами и закрепленных опорными устройствами.
Обозначим: 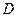 - число дисков пространственной или плоской стержневой системы,
- число дисков пространственной или плоской стержневой системы, 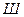 -число простых сферических шарниров, объединяющих диски в пространстве,
-число простых сферических шарниров, объединяющих диски в пространстве, 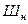 - число простых цилиндрических шарниров, объединяющих плоские диски,
- число простых цилиндрических шарниров, объединяющих плоские диски, 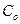 - число опорных связей стержневой системы.
- число опорных связей стержневой системы.
Составим формулы для определения общего числа степеней свободы пространственных стержневых систем, образованных по первому варианту.
Все диски пространственной системы имеют 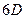 степеней свободы. Все сферические шарниры отбирают у дисков
степеней свободы. Все сферические шарниры отбирают у дисков 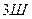 степеней свободы, и все опорные связи отбирают у дисков
степеней свободы, и все опорные связи отбирают у дисков 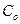 степеней свободы. Тогда общее число степеней свободы пространственной системы будет определяться по формуле:
степеней свободы. Тогда общее число степеней свободы пространственной системы будет определяться по формуле:
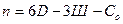 (1.2)
(1.2)
Аналогично составляется формула (1.3) для определения общего числа степеней свободы плоской стержневой системы, образованной по первому варианту.
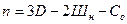 (1.3)
(1.3)
Стержневые системы, образованные по второму варианту состоят из нескольких узлов, объединенных между собой стержнями и закрепленных опорными устройствами.
Обозначим: 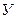 - общее число шарнирных улов пространственной или плоской системы,
- общее число шарнирных улов пространственной или плоской системы, 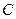 - число стержней, объединяющих узлы между собой,
- число стержней, объединяющих узлы между собой, 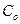 - число опорных связей стержневой системы.
- число опорных связей стержневой системы.
Шарнирный узел в пространстве имеет три степени свободы, а на плоскости две степени свободы. Стержень в пространстве или на плоскости, объединяя два узла, отбирает у них одну степень свободы. Все опорные связи отбирают у системы 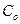 степеней свободы.
степеней свободы.
Учитывая сказанное, легко составить формулы для определения общего числа степеней свободы пространственной и плоской стержневой системы, образованной по второму варианту:
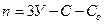 (1.4)
(1.4)
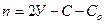 (1.5)
(1.5)
Дата добавления: 2019-04-03; просмотров: 500;
