Универсальная формула Мора для определения упругих перемещений.
Рассмотрим два состояния упругой балки. В состоянии 1 балка загружена произвольными силами, а в состоянии 2 она загружена только одной единичной силой 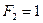 (рис.6.6).
(рис.6.6).
В первом состоянии возникает упругое перемещение 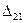 по направлению единичной силы второго состояния, любом поперечном сечении возникают внутренние усилия
по направлению единичной силы второго состояния, любом поперечном сечении возникают внутренние усилия 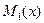 ,
, 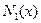 ,
, 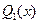 .
.
В любом поперечном сечении второго состояния возникают единичные внутренние усилия 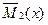 ,
, 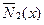 ,
, 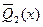 .
.
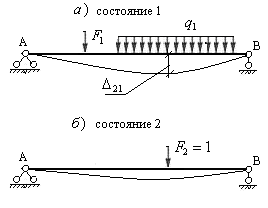
Рис.6.6
Согласно теореме о взаимности работ внешних сил и внутренних усилий второго состояния на соответствующих им перемещениях первого состояния, имеем:
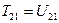 ,
,
но 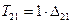 ,
,
а 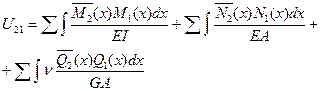
Тогда:
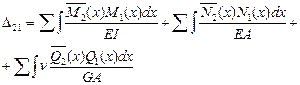 (6.21)
(6.21)
При вычислении перемещений в балочных или рамных стержневых системах по формуле Мора (6.21) учитывают влияние только изгибающих моментов, т.е. используют только первое слагаемое правой части этой формулы.
При вычислении перемещений в фермах по формуле Мора (6.21) учитывают влияние только продольных сил, т.е. используют только второе слагаемое правой части этой формулы.
Пример 6.1 Вычислить угол поворота правого опорного сечения однопролетной балки на двух шарнирных опорах, загруженной равномерно распределенной нагрузкой и имеющей постоянную жесткость 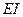 по всей длине (рис.6.7).
по всей длине (рис.6.7).
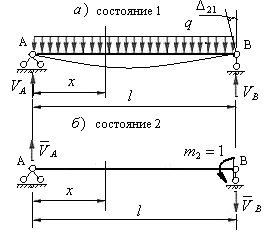
Рис.6.7
Решение: 1) Заданную балку принимаем как состояние 1, вычисляем реакции опор и составляем уравнение изгибающих моментов в произвольном сечении.
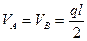 ,
, 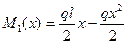
2) Создаем возможное состояние 2 путем загружения той же балки одним сосредоточенным единичным моментом 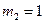 . Определяем реакции опор и составляем уравнение изгибающих моментов в этом состоянии.
. Определяем реакции опор и составляем уравнение изгибающих моментов в этом состоянии.
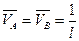 (направления реакций показаны на рис.6.7,б),
(направления реакций показаны на рис.6.7,б), 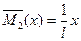
Уравнения изгибающих моментов в двух состояниях справедливы в интервале изменения переменной 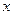 от нуля до
от нуля до 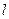 . Следовательно, имеем один участок интегрирования.
. Следовательно, имеем один участок интегрирования.
3) Вычисляем угол поворота правого опорного сечения балки, используя первое слагаемое правой части формулы Мора.
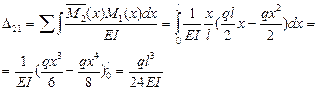
Дата добавления: 2019-04-03; просмотров: 735;
