Приемы определения внутренних усилий в заданной раме. Построение эпюр , , .
После вычисления неизвестных усилий в освобожденных «лишних» связях заданной рамы, можно определить изгибающие моменты, поперечные и продольные силы для каждого стержня и построить эпюры этих усилий.
При этом можно использовать два приёма:
1) Приём, основанный на применении метода сечений для построения эпюр внутренних усилий в статически определимых системах.
При его использовании необходимо основную систему метода сил загрузить заданными нагрузками и найденными из решения канонических уравнений значениями «лишних» неизвестных усилий в освобожденных связях. Разделить эту систему на участки, выбрать в пределах каждого из них произвольные сечения на переменных расстояниях от принятых начал координат, составить уравнения изгибающих моментов, поперечных и продольных сил и построить их графики, т.е эпюры соответствующих усилий.
Таким образом, определение внутренних усилий (изгибающих моментов, поперечных и продольных сил) и построение эпюр этих усилий осуществляется одновременно.
2) Приём, основанный на применении принципа независимости действия нагрузок.
Сначала осуществляется построение эпюры изгибающих моментов в заданной статически неопределимой раме.
Для этого следует построить исправленные эпюры изгибающих моментов в основной системе метода сил. Исправленные эпюры получают умножением ординат единичных эпюр на найденные значения соответствующих «лишних» неизвестных. Затем вычисляют ординаты эпюры изгибающих моментов в характерных сечениях заданной рамы. Они равны алгебраической сумме ординат грузовой эпюры и всех исправленных эпюр в тех же сечениях основной системы.
Таким образом, ординаты эпюры изгибающих моментов в произвольном сечении заданной рамы вычисляется по формуле:
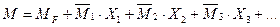 (7.14)
(7.14)
После построения эпюры изгибающих моментов вычисляют поперечные силы и строят эпюру 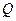 .
.
При вычислении поперечных сил на отдельных участках стержней заданной рамы следует использовать дифференциальные зависимости между изгибающим моментом, поперечной силой и интенсивностью внешней нагрузки. Из этих зависимостей следует, что на участках заданной рамы, где эпюра изгибающих моментов прямолинейная, поперечная сила имеет постоянное значение, равное тангенсу угла наклона эпюры изгибающих моментов к оси стержня, т.е.
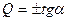 (7.15)
(7.15)
Верхний знак формулы (7.15) принимается в том случае, когда до совмещения с осью стержня эпюру изгибающих моментов следует повернуть против часовой стрелки. Нижний знак той же формулы принимается в том случае, когда до совмещения с осью стержня эпюру изгибающих моментов следует повернуть по часовой стрелке.
На рис.7.5 показан участок рамы 1-2, на котором эпюра изгибающих моментов прямолинейна. Вычислим поперечную силу на этом участке, используя формулу (7.15) и построим эпюру 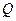 .
.
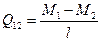 (7.16)
(7.16)
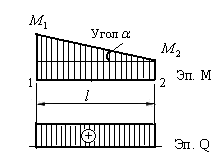
Рис.7.5
На участках рамы, загруженных равномерно распределенной нагрузкой, поперечные силы непрерывно меняются по длине, следуя линейной зависимости. Эпюра поперечных сил на таких участках может быть построена по двум ординатам, вычисленным для концевых сечений участка стержня по методу равновесия дисков. Для этого вырезают диск, загружают его распределенной нагрузкой 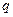 ,
,
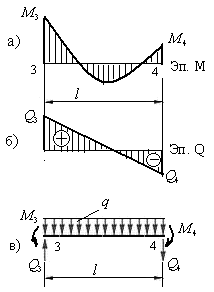
Рис.7.6
изгибающими моментами 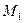 и
и 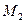 , величины и направления которых устанавливают по эпюре
, величины и направления которых устанавливают по эпюре 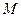 , а так же неизвестными поперечными силами в граничных сечениях участка. Эти силы направляют так, чтобы они вращали стержень по часовой стрелке. В этом случае поперечные силы будут иметь истинные знаки.
, а так же неизвестными поперечными силами в граничных сечениях участка. Эти силы направляют так, чтобы они вращали стержень по часовой стрелке. В этом случае поперечные силы будут иметь истинные знаки.
Используя два условия равновесия диска, составляют уравнения равновесия и вычисляют неизвестные поперечные силы, позволяющие построить эпюру 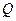 . На рис.7.6,а показана возможная эпюра изгибающих моментов на участке 3-4 рамы, загруженном распределенной нагрузкой
. На рис.7.6,а показана возможная эпюра изгибающих моментов на участке 3-4 рамы, загруженном распределенной нагрузкой 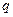 .
.
На рис.7.6,в показаны все нагрузки, действующие на участок 3-4 стержня рамы. Составим уравнения его равновесия:
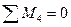

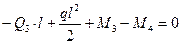

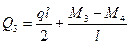 (7.17)
(7.17)
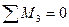

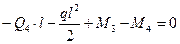

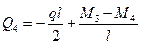 (7.18)
(7.18)
Продольные силы в стержнях заданной рамы определяются по методу равновесия узлов. Для этого сначала вырезают узлы, объединяющие два стержня, загружают их заданными сосредоточенными силами (если они приложены к узлам рамы), неизвестными продольными силами в рассеченных стержнях и поперечными силами в тех же стержнях.
Величины и направления поперечных сил устанавливаются по эпюре поперечных сил. Если поперечная сила имеет знак плюс, то её направляют так, чтобы она вращала узел по часовой стрелке. Если же поперечная сила имеет знак минус, то её направляют так, чтобы она вращала узел против часовой стрелки. Для каждого узла составляют два уравнения равновесия, используя рациональные условия (аналогично как при определении усилии в стержнях ферм).
Затем вырезают узлы рамы, объединяющие три стержня, усилие в одном из которых уже вычислено, загружают аналогично предыдущим узлам, составляют уравнения равновесия и вычисляют неизвестные продольные усилия.
При построении эпюры продольных усилий принято откладывать ординаты перпендикулярно к осям стержней в обе стороны от них. Таким образом, оси стержней будут являться средними линиями эпюры 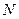 .
.
Дата добавления: 2019-04-03; просмотров: 812;
