Примеры расчета статически неопределимых рам методом сил
Пример 7.1: для рамы с заданными размерами и нагрузками (рис.2) требуется:
а) построить эпюры изгибающих моментов, поперечных и продольных сил;
б) проверить правильность построенных эпюр.
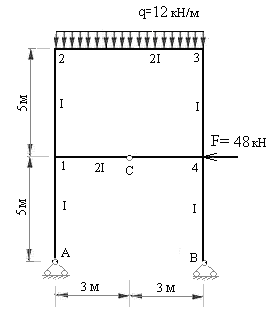
Рис.7.7
Последовательность решение задачи:
1) Устанавливаем степень статической неопределимости рамы по формуле: 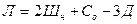 . Для заданной рамы имеем:
. Для заданной рамы имеем: 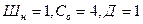 , тогда
, тогда 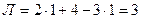 , т.е. рама три раза статически неопределима.
, т.е. рама три раза статически неопределима.
2) Выбираем основную систему метода сил путем освобождения трех лишних связей. За лишние связи можно принимать любые связи заданной рамы при условии, что после их освобождения (удаления) основная система будет статически определимой и неподвижной на плоскости.
Для любой статически неопределимой рамы можно образовать несколько вариантов основной системы. Чем выше степень статической неопределимости рамы, тем больше вариантов основной системы возможно предложить. На рисунках 7.8,а; 7.8,б; 7.8,в; 7.8,г показаны четыре варианта основной системы, которые могут быть приняты при расчете заданной рамы методом сил.
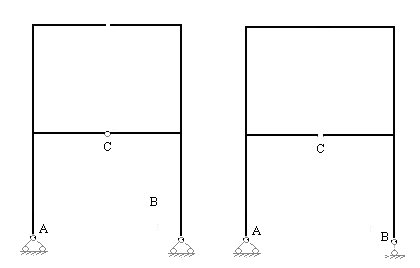
Рис.7.8,а Рис.7.8,б
Первый вариант основной системы (рис.7.8,а) образуем рассечением ригеля второго этажа заданной рамы (рассечь ригель можно в любом месте, как посредине пролета, так и вблизи одного из жестких узлов). Рассекая стержень на две части, освобождаем три связи:
- связь, препятствующую взаимному горизонтальному перемещению разъединенных частей стержня;
- связь, препятствующую взаимному вертикальному перемещению разъединенных частей стержня;
- связь, препятствующую взаимному повороту торцов, проведенного поперечного сечения стержня.
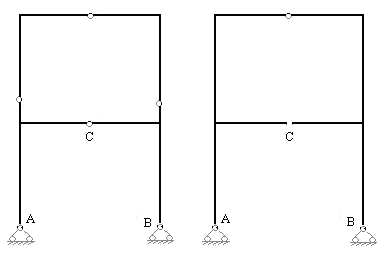
Рис.7.8.в Рис.7.8,г
Второй вариант основной системы (рис.7.8,б) выбираем путем удаления связей шарнира С заданной рамы (шарнир имеет две связи) и одной опорной связи на горизонтальное перемещение.
Третий вариант основной системы (рис.7.8,в) образуем введением трех цилиндрических шарниров в сечения ригеля и стоек второго этажа заданной рамы. Напомним, что введением шарнира в произвольное сечение стержня освобождается одна связь на взаимное угловое перемещение поперечных сечений, объединяемых шарниром.
Четвертый вариант основной системы (рис.7.8,г) образуем освобождением двух связей шарнира С и введение шарнира в среднее сечение ригеля второго этажа заданной рамы.
Примечание: при образовании основной системы вводить шарниры или рассекать стержни можно в произвольных местах. Однако, если заданная рама имеет ось геометрической и жесткостной симметрий, то упрощение расчета будет достигнуто при выборе симметричной основной системы. Все четыре варианта основной системы выбраны симметричными относительно вертикальной оси, проходящей через шарнир С заданной рамы.
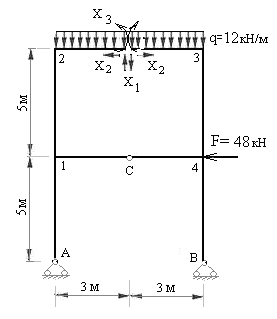
Рис.7.9
Принимаем для расчета рамы первый вариант основной системы (рис.7.8,а).
3) Образуем эквивалентную систему. Для этого основную систему загружаем заданными нагрузками и неизвестными усилиями 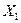 ,
, 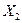 и
и 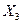 , которые компенсируют действие на раму освобожденных связей в поперечном сечении ригеля второго этажа (рис.7.9).
, которые компенсируют действие на раму освобожденных связей в поперечном сечении ригеля второго этажа (рис.7.9).
4) Записываем систему канонических уравнений метода сил:
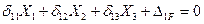
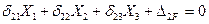 (7.19)
(7.19)
5) Строим единичные эпюры, а также грузовую эпюру изгибающих моментов в основной системе метода сил (рис.7.10,7.11, 7.12 и 7.13).
Для построения эпюр изгибающих моментов необходимо:
- определить реакции опор (величины и направления этих реакций от каждого вида нагрузки определяются из условий равновесия рамы в целом и отдельных дисков);
- вычислить изгибающие моменты в характерных сечениях каждого стержня;
- отложить их от оси каждого стержня в сторону растянутой зоны и соединить прямыми или кривыми линиями.
На рисунках 7.10-7.13 показаны направления и величины реакций опор и построены единичные эпюры и грузовая эпюра изгибающих моментов. Предлагаем изучающим курс составить необходимые уравнения равновесия и проверить найденные значения реакций и их направления.
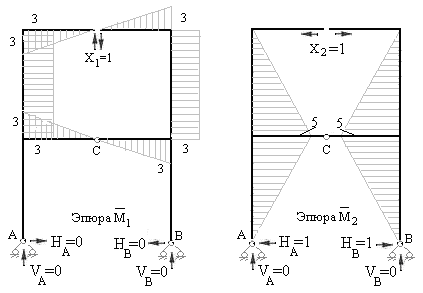
Рис.7.10 Рис.7.11
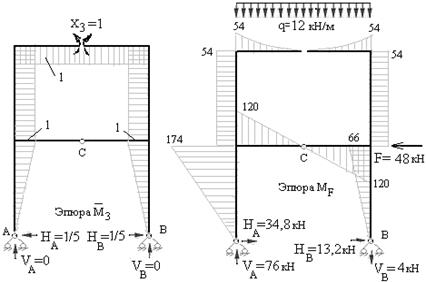
Рис.7.12 Рис.7.13
6) Определяем коэффициенты и грузовые перемещения канонических уравнений метода сил, пользуясь правилом Верещагина. Напомним, что перемножение эпюр изгибающих моментов осуществляется на каждом участке рамы, в пределах которого одна из двух перемножаемых эпюр прямолинейна, а вторая может иметь произвольное очертание и может быть разделена на части, площади и положения центров тяжести которых, легко определяются.
Единичные эпюры изгибающих моментов всегда имеют прямолинейное очертание в пределах отдельных стержней рамы. Поэтому коэффициенты канонических уравнений легко вычисляются по правилу Верещагина.
Вычислим, к примеру, коэффициент δ11. Для этого необходимо перемножить эпюру 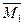 саму на себя, т.е. на каждом участке вычислить площадь эпюры, найти её ординату под собственным центром тяжести, перемножить эти величины и разделить на жесткость рассматриваемого участка рамы. Результаты перемножения на каждом участке алгебраически сложить.
саму на себя, т.е. на каждом участке вычислить площадь эпюры, найти её ординату под собственным центром тяжести, перемножить эти величины и разделить на жесткость рассматриваемого участка рамы. Результаты перемножения на каждом участке алгебраически сложить.
Как видно из рисунка 7.10 эпюра 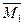 состоит из четырех одинаковых треугольников (жесткость рамы на этих участках также одинакова и равна 2EI) и двух одинаковых прямоугольников (жесткость рамы на этих участках также одинакова и равна EI). Тогда, применяя правило Верещагина, найдем:
состоит из четырех одинаковых треугольников (жесткость рамы на этих участках также одинакова и равна 2EI) и двух одинаковых прямоугольников (жесткость рамы на этих участках также одинакова и равна EI). Тогда, применяя правило Верещагина, найдем:
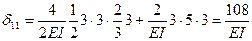 ;
;
Перемножая аналогично эпюры 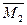 и
и 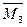 , найдем главные коэффициенты δ22 и δ33:
, найдем главные коэффициенты δ22 и δ33:
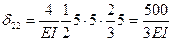 ;
;
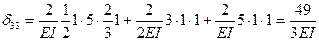 .
.
Необходимо помнить, что главные коэффициенты канонических уравнений всегда имеют положительные значения, так как площади и ординаты перемножаемых эпюр имеют один и тот же знак.
Вычисляем побочные коэффициенты канонических уравнений. Для этого перемножаем по правилу Верещагина единичные эпюры, имеющие разные индексы. Например, коэффициенты δ12=δ21 определяем перемножением единичных эпюр: 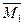 и
и 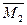 . Побочные коэффициенты могут иметь положительные, отрицательные или нулевые значения. Анализируя указанные эпюры, устанавливаем, что их перемножение следует выполнить на двух верхних стойках рамы.
. Побочные коэффициенты могут иметь положительные, отрицательные или нулевые значения. Анализируя указанные эпюры, устанавливаем, что их перемножение следует выполнить на двух верхних стойках рамы.
На левой стойке эпюры 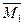 и
и 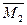 расположены по одну сторону от оси (справа), а на правой стойке эти эпюры расположены по разные стороны от её оси. Результат перемножения эпюр
расположены по одну сторону от оси (справа), а на правой стойке эти эпюры расположены по разные стороны от её оси. Результат перемножения эпюр 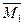 и
и 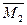 по правилу Верещагина на левой стойке будет иметь знак плюс, а результат перемножения этих эпюр на правой стойке будет иметь такую же величину и знак минус. Алгебраическая сумма указанных результатов перемножения будет равной нулю.
по правилу Верещагина на левой стойке будет иметь знак плюс, а результат перемножения этих эпюр на правой стойке будет иметь такую же величину и знак минус. Алгебраическая сумма указанных результатов перемножения будет равной нулю.
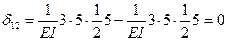
Следовательно, единичные перемещения 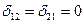 .
.
Примечание: Эпюра 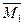 имеет косую симметрию относительно вертикальной оси, проведенной через середины ригелей рамы, а эпюра
имеет косую симметрию относительно вертикальной оси, проведенной через середины ригелей рамы, а эпюра 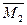 является симметричной относительно той же оси. Результат перемножения таких эпюр всегда равен нулю.
является симметричной относительно той же оси. Результат перемножения таких эпюр всегда равен нулю.
Напомним, что результат перемножения двух эпюр на любом участке имеет положительный знак, если они расположены с одной стороны от оси стержня и отрицательный знак, если они расположены по разные стороны от оси стержня.
Эпюра 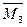 является симметричной, аналогично эпюре
является симметричной, аналогично эпюре 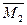 . Поэтому результат перемножения её на эпюру
. Поэтому результат перемножения её на эпюру 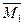 будет равным нулю, т.е.
будет равным нулю, т.е. 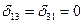 .
.
Вычислим побочные коэффициенты δ23=δ32, перемножая единичные эпюры 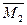 и
и 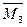 :
:
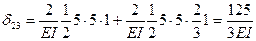
Определяем грузовые перемещения, перемножением грузовой эпюры на каждую из единичных эпюр. При этом используем свойство прямой и косой симметрии эпюр на отдельных участках.
Перемножаем эпюру 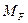 на эпюру
на эпюру 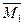 в пределах нижнего ригеля:
в пределах нижнего ригеля:
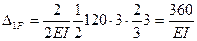 ;
;
Перемножаем эпюру 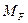 на эпюру
на эпюру 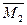 на всех стойках:
на всех стойках:
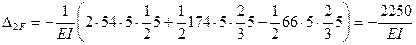 .
.
Перемножаем эпюру 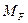 на эпюру
на эпюру 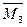 на всех стойках и верхнем ригеле:
на всех стойках и верхнем ригеле:
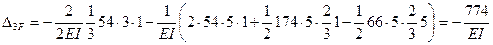 .
.
7) Определяем значения неизвестных усилий в освобожденных связях заданной рамы из решения канонических уравнений:
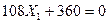
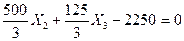 (7.20)
(7.20)
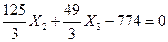
Из первого уравнения системы (7.20) находим 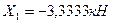
Из решения второго и третьего уравнений системы (7.20), находим:
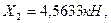
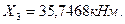
.
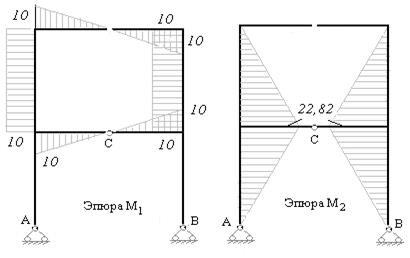
Рис.7.14 Рис.7.15
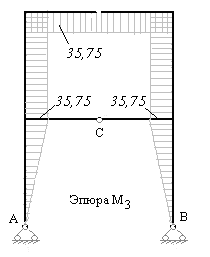
Рис.7.16
8) Строим исправленные эпюры изгибающих моментов в основной системе. Для этого умножаем ординаты единичных эпюр на найденные (из решения канонических уравнений) значения неизвестных усилий. На рис.7.14 – 7.15 построены исправленные эпюры изгибающих моментов (используем второй приём построения эпюры изгибающих моментов).
9) Строим эпюру изгибающих моментов в заданной статически неопределимой раме. Для этого в характерных сечениях рамы алгебраически суммируем ординаты трех эпюр изгибающих моментов, построенных в основной системе: грузовой эпюры 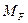 и трех исправленных эпюр
и трех исправленных эпюр 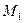 ,
, 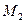 и
и 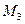 . На рис.7.17 построена эта эпюра.
. На рис.7.17 построена эта эпюра.
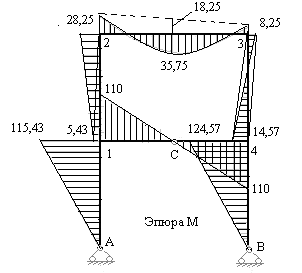
Рис.7.17
10) Проверяем правильность построенной эпюры изгибающих моментов в заданной раме:
а) статическая проверка по условиям равновесия жестких узлов рамы от действия узловых моментов. По эпюре видно, что все четыре жесткие узлы рамы 1.2.3 и 4 находятся в равновесии, т.е. сумма узловых изгибающих моментов в каждом жестком узле равна нулю;
б) деформационная проверка состоит в том, что перемещение в раме по направлению любой неизвестной метода сил должно быть равным нулю
Найдем, например, перемещение по направлению 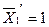 (рис.7.18), во втором варианте основной системы. Для этого построим единичную эпюру изгибающих моментов
(рис.7.18), во втором варианте основной системы. Для этого построим единичную эпюру изгибающих моментов 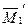 и перемножим по правилу Верещагина эпюру
и перемножим по правилу Верещагина эпюру 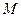 на единичную эпюру
на единичную эпюру 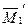 . Предварительно сложные эпюры расчленяем на простые так, чтобы их площади и положения центров тяжести легко определялись. На рис.7.17 и 7.18 показано разделение сложных эпюр на простые эпюры. Криволинейная эпюра на верхнем ригеле разделена на параболический сегмент, имеющий ординату 54 по середине ригеля и трапецию. На стойках трапеции разделены на два треугольника. Тогда:
. Предварительно сложные эпюры расчленяем на простые так, чтобы их площади и положения центров тяжести легко определялись. На рис.7.17 и 7.18 показано разделение сложных эпюр на простые эпюры. Криволинейная эпюра на верхнем ригеле разделена на параболический сегмент, имеющий ординату 54 по середине ригеля и трапецию. На стойках трапеции разделены на два треугольника. Тогда:
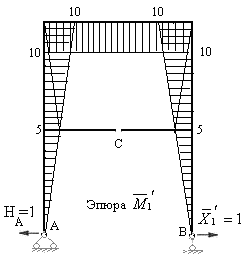
Рис.7.18
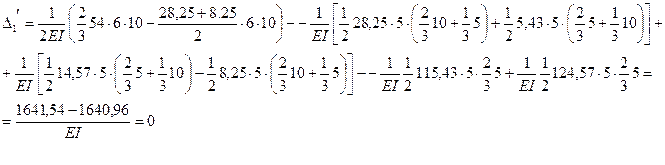 Таким образом, деформационная проверка выполняется. Следовательно, эпюра изгибающих моментов в заданной раме построена правильно.
Таким образом, деформационная проверка выполняется. Следовательно, эпюра изгибающих моментов в заданной раме построена правильно.
11) Используя правило Журавского, определяем поперечные силы на участках рамы, где эпюра М прямолинейна. Рама имеет пять таких участков:
Участок А-1. 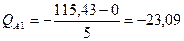 кН.
кН.
Участок 1-2. 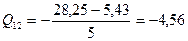 кН.
кН.
Участок 1-4. 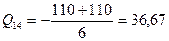 кН.
кН.
Участок 3-4. 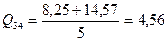 кН.
кН.
Участок 4-В. 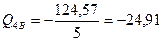 кН.
кН.
Определяем поперечные силы на концах участка 2-3, загруженного равномерно распределенной нагрузкой. Для этого используем формулы (7.17) и (7.18):
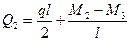 ,
,
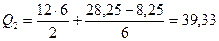 кН.
кН.
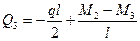
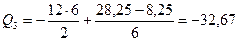 кН.
кН.
На рис.7.19 построена эпюра поперечных сил. Поперечные силы со знаком плюс отложены вверх от осей каждого ригеля рамы, и влево от осей каждой стойки. Поперечные силы со знаком минус откладываются противоположно.
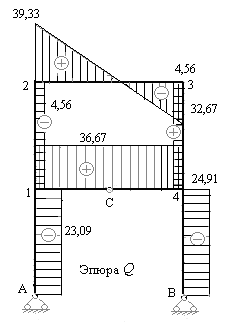
Рис.7.19
12) Определяем продольные силы в стержнях рамы, пользуясь методом равновесия узлов. Вырезаем сначала узлы 2 и 3, а затем узлы 1 и 4. Эти узлы загружаем неизвестными продольными усилиями, направленными от узлов, и известными поперечными силами в рассеченных стержнях. Величины и направления поперечных сил устанавливаются по эпюре поперечных сил (рис.13). Поперечная сила, имеющая знак плюс должна вращать узел по часовой стрелке, а поперечная сила, имеющая знак минус должна вращать узел против часовой стрелки. На рис.14 показаны все силы, действующие на каждый узел рамы.
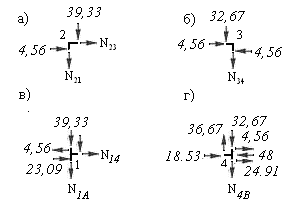
Рис.7.20
Для каждого узла рамы составляем два уравнения равновесия, используя следующие два условия:
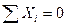 и
и 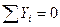 .
.
Узел 2 (рис.7.20,а):
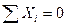 ,
, 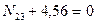 ,
, 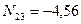 кН.
кН.
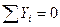 ,
, 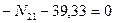 ,
, 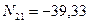 кН.
кН.
Узел 3 (рис.7.20,б):
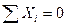 ,
, 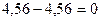 ,
, 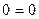 (проверка).
(проверка).
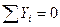 ,
, 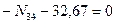 ,
, 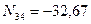 кН.
кН.
Узел 1 (рис.7.20,в):
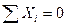 ,
, 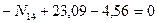 ,
, 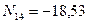 кН.
кН.
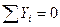 ,
, 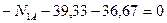 ,
, 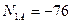 кН.
кН.
Узел 4 (рис.7.20,г):
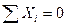 ,
, 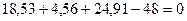 ,
, 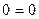 (проверка).
(проверка).
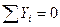 ,
, 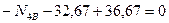 ,
, 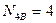 кН.
кН.
Эпюра продольных сил построена на рис.7.21.
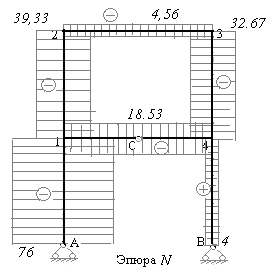
Рис.7.21
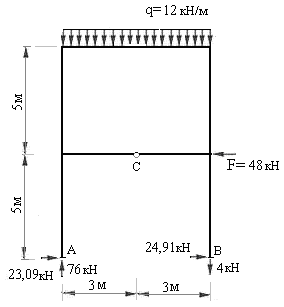
Рис.7.22
13) Проверяем равновесие рамы в целом. Освобождаем раму от опор и загружаем её заданными нагрузками и реакциями освобожденных опорных
связей (рис.7.22)
Величины и направления этих реакций устанавливаем по эпюрам поперечных и продольных сил (рис.7.19 и 7.21).
Составляем три уравнения равновесия рамы, используя условия:
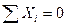 ,
, 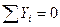 ,
, 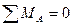
1) 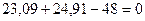 ;
; 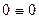
2) 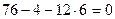 ;
; 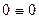
3) 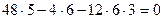 ,
, 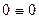
Таким образом, все уравнения равновесия удовлетворяются. Расчет рамы методом сил выполнен без ошибок.
Пример 7.2: Построить эпюры внутренних усилий для статически неопределимой рамы с наклонным ригелем и вертикальными стойками, защемленными у основания (рис.7.23). Жесткости стоек принять равными 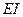 , жесткость ригеля равной
, жесткость ригеля равной 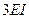 .
.
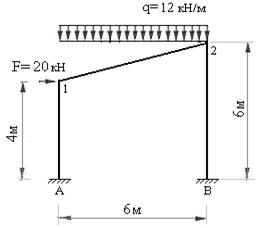
Рис.7.23
Последовательность расчета:
1. Устанавливаем степень статической неопределимости заданной рамы, используя формулу (1.1).
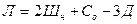 ;
; 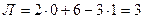 .
.
Таким образом, заданная рама имеет три независимых неизвестных метода сил.
2. Образуем основную систему метода сил. Из всех возможных основных систем, которые предлагаем образовать самостоятельно, выберем расчетную основную систему путем вертикального разреза ригеля в узле 1 заданной рамы (рис.7.24,а). Эта система является статически определимой и состоит из двух неподвижных и геометрически неизменяемых частей: левой стойки А-1 и ломаного стержня 1-2-В.
3. Создаем эквивалентную систему метода сил. Для этого основную систему загружаем заданными нагрузками и неизвестными усилиями 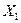
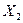 и
и 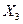 (рис. 7.24,б)
(рис. 7.24,б)
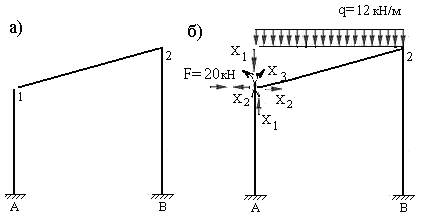
Рис.7.24
4. Записываем систему канонических уравнений метода сил:
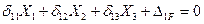
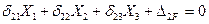 (7.21)
(7.21)
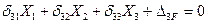
5. Строим единичные эпюры и грузовую эпюру изгибающих моментов в основной системе.
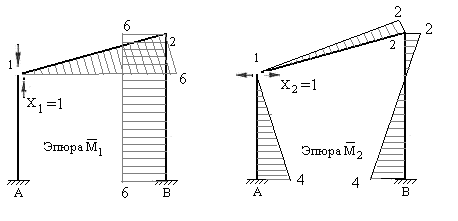
Рис.7.25 Рис.7.26
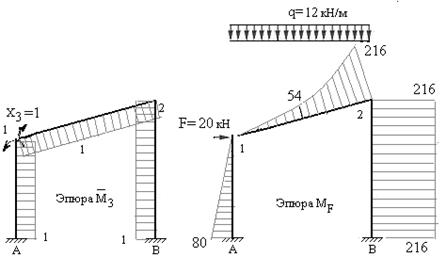
Рис.7.27 Рис.7.28
В отличие от рамы, рассмотренной в примере 1, эти эпюры можно построить, не определяя реакции, которые возникают в защемляющих опорах от заданных нагрузок. Изгибающие моменты определяются по участкам, рассматриваемым от проведенного сечения (разреза) рамы к опорам. На рисунках 7.25-7.28 построены единичные эпюры и грузовая эпюра изгибающих моментов в основной системе. При этом ординаты эпюр отложены перпендикулярно осям стержней со стороны растянутых волокон.
6. Определяем коэффициенты и грузовые перемещения канонических уравнений, пользуясь правилом Верещагина.
Примечание: При перемножении эпюр изгибающих моментов по правилу Верещагина учитывается истинная длина каждого стержня или каждого участка.
Вычислим предварительно длину наклонного ригеля.
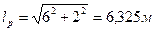 . Тогда найдем:
. Тогда найдем:
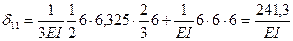
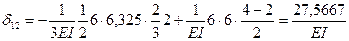
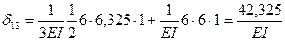
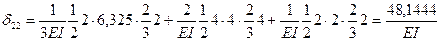
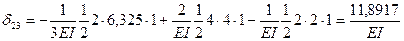
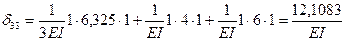
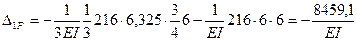
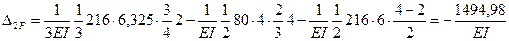
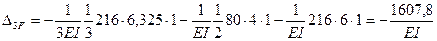
7. Подставляем эти значения в канонические уравнения, переносим грузовые перемещения в правые части и решаем полученную систему уравнений методом уравнивания коэффициентов при неизвестных:
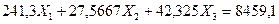
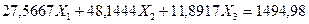 (7.22)
(7.22)
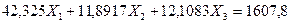
Разделим каждое уравнение на коэффициенты при неизвестном усилии 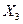 :
:
аждое уравнение на коэффициенты при 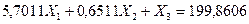 ий авнивания коэффициентов при неовые перемещения в правые части и
ий авнивания коэффициентов при неовые перемещения в правые части и
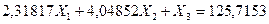 (7.23)
(7.23)
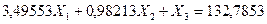
Вычитаем из первого уравнения системы (7.23) второе, а затем третье, получаем новую систему двух уравнений с двумя неизвестными:
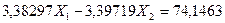
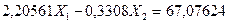 (7.24)
(7.24)
Уравниваем коэффициенты при неизвестном усилии 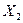 и вычитаем первого полученного уравнения второе:
и вычитаем первого полученного уравнения второе:
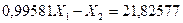
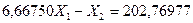 (7.25)
(7.25)
Вычитаем из второго уравнения системы (7.25), первое, находим неизвестное усилие 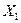 :
: 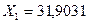 кН. Из первого уравнения системы (7.25) определяем величину неизвестного усилия
кН. Из первого уравнения системы (7.25) определяем величину неизвестного усилия 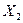 :
: 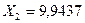 кН. Для проверки правильности вычислений следует подставить во второе уравнения системы (7.25) и убедиться, что оно обращается в тождество
кН. Для проверки правильности вычислений следует подставить во второе уравнения системы (7.25) и убедиться, что оно обращается в тождество 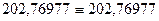 .
.
Из первого уравнения системы (7.23) определяем величину усилия 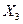 :
:
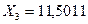 кНм. При подстановке всех найденных значений неизвестных усилий во второе и третье уравнения системы (7.23) они должны тождественно удовлетворяться, аналогично предыдущему.
кНм. При подстановке всех найденных значений неизвестных усилий во второе и третье уравнения системы (7.23) они должны тождественно удовлетворяться, аналогично предыдущему.
8. Строим исправленные эпюры изгибающих моментов в основной системе путем умножения ординат единичных эпюр на значения усилий, полученные из решения канонических уравнений метода сил (рис.7,29 – 7.31).
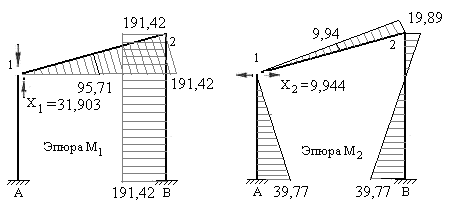
Рис.7.29 Рис.7.30
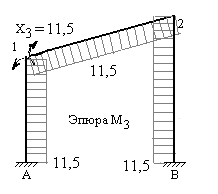
Рис.7.31
Так как все три усилия имеют знак плюс, то их направления, принятые предварительно, верны и исправленные эпюры будут полностью совпадать по виду с единичными эпюрами. Ординаты исправленных эпюр получаем умножением ординат единичных эпюр на значения соответствующих усилий.
9. Строим эпюру изгибающих моментов в заданной статически неопределимой раме. Для этого суммируем ординаты грузовой эпюры и трех исправленных эпюр, построенных в основной системе метода сил, т.е. эпюр, построенных на рис. 7.28 – 7.31. На рис.7.32 построена эпюра изгибающих моментов в заданной раме. Легко подсчитать величины ординат этой эпюры и убедиться в правильности её построения.
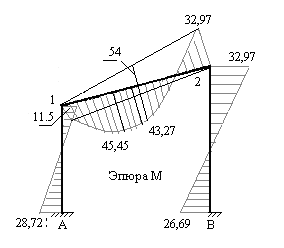
Рис.7.32
10. Осуществим статическую и деформационную проверки эпюры изгибающих моментов.
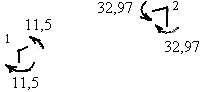
Рис.7.33
а) Статическая проверка состоит в том, что жесткие узлы рамы 1 и 2 должны находиться в равновесии под действием узловых изгибающих моментов.
Вырезаем жесткие узлы рамы 1 и 2. На эти узлы действуют изгибающие моменты, величины и направления которых, определяем по эпюре изгибающих моментов (моменты действуют из растянутой зоны в сторону сжатой зоны стержней). На рис.7.33 показано загружение узлов узловыми изгибающими моментами. Легко убедиться, что алгебраическая сумма моментов, действующих на каждый узел равна нулю.
б) Деформационная проверка. Выбираем новый вариант основной системы путем замены защемляющих опор рамы шарнирно неподвижными и введения шарнира в узел 2 заданной рамы. В результате получаем трехшарнирную раму (рис.7.34).
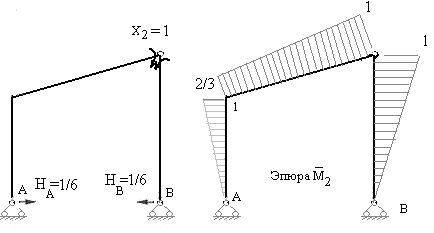
Рис. 7.34 Рис.7.35
Загрузим её единичными моментами 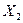 =1, вычислим горизонтальные реакции опор и построим единичную эпюру
=1, вычислим горизонтальные реакции опор и построим единичную эпюру 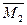 в этой системе (рис.7.35).
в этой системе (рис.7.35).
При перемножении эпюр (рис.7,32) и (рис.7.35) рассматриваем три стержня. На стойках А-1 и В-2 эпюры прямолинейные и их перемножение не вызывает трудностей. На ригеле 1-2 эпюра (рис.7.32) криволинейная, но она может быть разделена на три простые фигуры, площади и положения центров тяжести которых, легко определяются. Этими фигурами являются:
1) квадратичная парабола, имеющая основанием ригель длиною 6,325 м. и максимальную ординату посредине его длины. Эта ордината равна 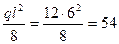 кНм. Площадь такой эпюры равна 2/3 произведения длины на максимальную ординату, а центр тяжести располагается посредине длины ригеля (ордината эпюры
кНм. Площадь такой эпюры равна 2/3 произведения длины на максимальную ординату, а центр тяжести располагается посредине длины ригеля (ордината эпюры 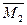 под центром тяжести эпюры М равна половине суммы её ординат на концах ригеля);
под центром тяжести эпюры М равна половине суммы её ординат на концах ригеля);
2) треугольника, расположенного сверху ригеля;
3) треугольника, расположенного снизу ригеля. Площади этих треугольников и положения их центров тяжести легко определяются, а следовательно, легко вычисляются необходимые ординаты единичной эпюры. Вычислим перемещение 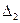 .
.
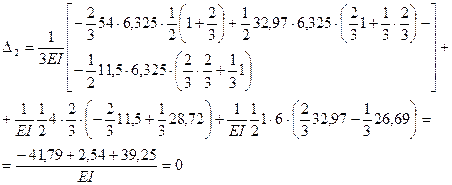
Таким образом, деформационная проверка выполняется. Эпюра изгибающих моментов в заданной раме построена правильно.
11. Определяем поперечные силы в каждом стержне рамы и строим эпюру этих сил.
На стойках рамы эпюра изгибающих моментов ограничена прямыми линиями, наклоненными к оси стержня. Тангенсы углов наклона этих прямых равны поперечным силам, т.е.
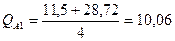 кН,
кН, 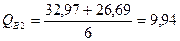 кН
кН
На ригеле 1-2 эпюра изгибающих моментов имеет криволинейное очертание по квадратичной зависимости, поэтому эпюра поперечных сил будет ограничена прямой, наклоненной к оси ригеля.
Для построения такой эпюры достаточно вычислить две её ординаты в сечениях 1 и 2 ригеля. Воспользуемся методом равновесия дисков. Вырезаем ригель 1-2 из рамы и загружаем его: заданной равномерно распределенной нагрузкой интенсивностью 12 кн/м, известными изгибающими моментами в сечениях 1 и 2 (их величины и направления устанавливаем по эпюре изгибающих моментов), а также неизвестными поперечными силами в сечениях 1 и 2 ригеля. Эти силы направляем перпендикулярно оси ригеля так, чтобы они вращали вырезанный стержень по часовой стрелке (рис.7.36).
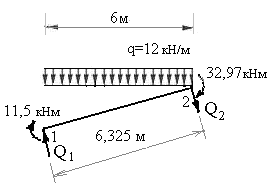
Рис.7.36
Составляем два уравнения равновесия стержня 1-2, используя рациональные условия равновесия:
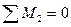

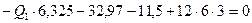

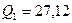 кН.
кН.
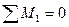

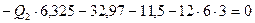

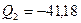 кН.
кН.
На рис.7.37 построена эпюра поперечных сил.
12. Определяем продольные силы в стержнях заданной рамы, пользуясь методом равновесия узлов.
Вырезаем узлы 1 и 2 рамы и загружаем их заданными нагрузками (к узлу 1 приложена сила 20 кн, направленная вправо), известными поперечными силами (величины и направления этих сил устанавливаем по эпюре поперечных сил), а также неизвестными продольными силами, которые
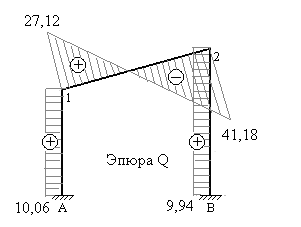
Рис.7.37
направляем от узлов (в соответствии с предполагаемым растяжением стержней). На рис.7.38 показано загружение узлов 1 и 2 заданной рамы.
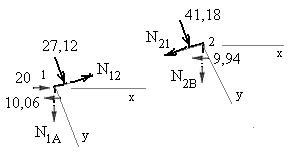
Рис.7,38
Выбираем для каждого узла систему координат так, чтобы одна из осей была перпендикулярной к одному неизвестному усилию, а другая ось перпендикулярна к другому неизвестному усилию. В этом случае уравнения равновесия будут разделенными относительно неизвестных.
Составляем уравнения равновесия узла 1:
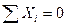

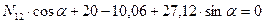 ,
,
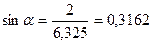
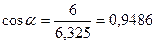 , тогда
, тогда
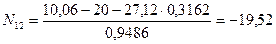 кН
кН
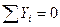

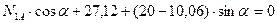 , тогда:
, тогда:
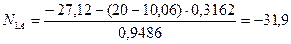 кН.
кН.
Составляем уравнения равновесия узла 2:
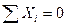

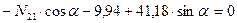 ,
,
откуда
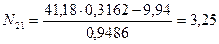 кН.
кН.
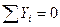

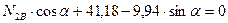 ,
,
откуда
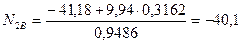 кН.
кН.
На рис.7.39 построена эпюра продольных сил для заданной рамы.
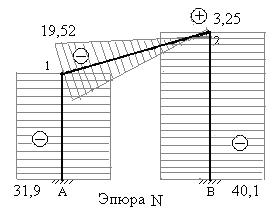
Рис.7.39
13. Проверяем равновесие рамы в целом.
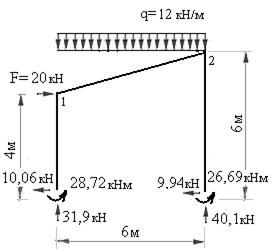
Рис.7.40
Для этого освобождаем её от опор и загружаем заданными нагрузками и реакциями опорных связей. Величины и направления реакций опор устанавливаем по эпюрам изгибающих моментов, поперечных и продольных сил. На рис.7.40 показано загружение рамы, при котором она должна удовлетворять трем условиям равновесия статики.
Составим уравнения равновесия и убедимся, что они тождественно удовлетворяются:
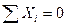

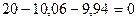

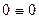
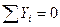

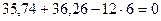

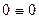
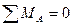

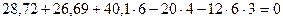

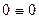
Таким образом, расчет заданной статически неопределимой рамы выполнен правильно.
Пример 7.3. Построить эпюры изгибающих моментов, поперечных и продольных сил для двухпролетной одноэтажной рамы при заданных нагрузках (рис.7.41).
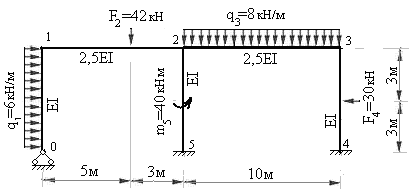 Рис.7.41
Рис.7.41
Последовательность расчета:
1. Устанавливаем степень статической неопределимости заданной рамы, используя формулу (1.1).
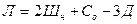 ;
; 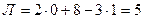 .
.
Таким образом, заданная рама имеет пять независимых неизвестных метода сил, т.е. она является пять раз статически неопределимой.
2. Образуем основную систему метода сил путем освобождения 5-ти лишних связей. На рис.7.42 показан расчетный вариант основной системы. 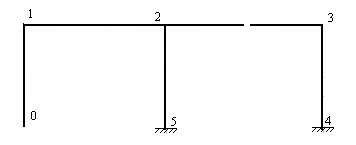
Рис.7.42
Чем выше степень статической неопределимости рамы, тем больше вариантов основной системы метода сил может быть образовано. Предлагаем образовать самостоятельно четыре варианта основной системы, а расчетный вариант основной системы образуем путем вертикального разреза ригеля 2-3 рамы посередине второго пролета и удаления шарнирно-неподвижной опоры 0 (рис.7.42). Эта система является статически определимой и состоит из двух неподвижных и геометрически неизменяемых частей: левого ломаного стержня, защемленного у основания 5 средней стойки и ломаного правого стержня, защемленного у основания 4 правой стойки.
3. Создаем эквивалентную систему метода сил. Для этого основную систему загружаем заданными нагрузками и неизвестными усилиями 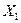 ,
, 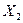 ,
, 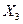 ,
, 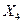 и
и 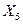 (рис 7.43).
(рис 7.43).
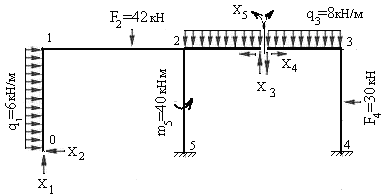
Рис.7.43
4. Записываем систему канонических уравнений метода сил:
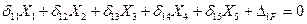
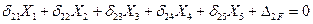
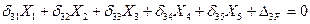 (7.25)
(7.25)
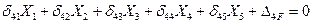
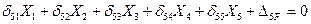
5. Строим единичные эпюры изгибающих моментов и грузовую эпюру в основной системе. Как в примере 2, эти эпюры можно построить, не определяя реакции, которые возникают в защемляющих опорах от заданных нагрузок. Изгибающие моменты определяются по участкам, рассматриваемым от свободных (не закрепленных) концов стержней к опорам.
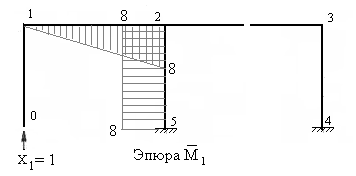
Рис.7.44
На рисунках 7.44 – 7.49 построены единичные эпюры и грузовая эпюра изгибающих моментов в основной системе. Напоминаем, что ординаты эпюр изгибающих моментов должны быть отложены перпендикулярно осям стержней со стороны растянутых волокон.
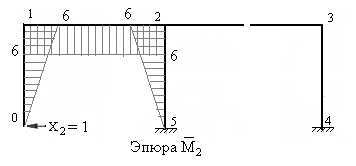
Рис.7.45
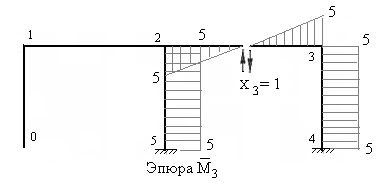
Рис.7.46
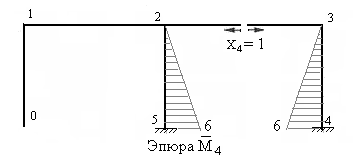
Рис.7.47
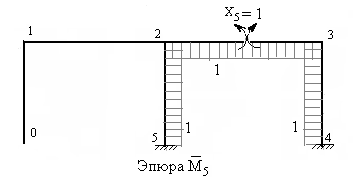
Рис.7.48
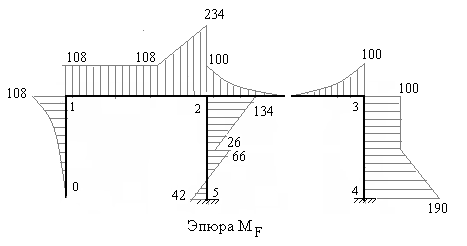
Рис.7.49
6. Определяем коэффициенты и грузовые перемещения канонических уравнений, пользуясь правилом Верещагина:
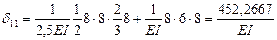 ,
,
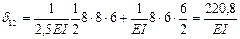 ,
,
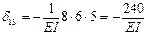 ,
, 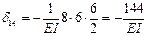 ,
,
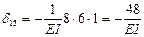 ;
;
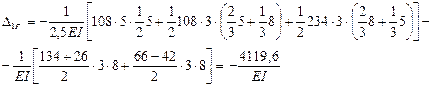
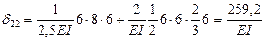 ,
, 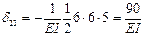 ,
,
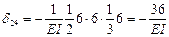 ,
, 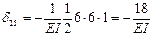 ;
;
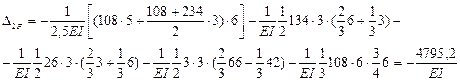
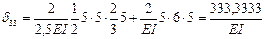 ,
,
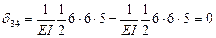 ,
,
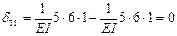 ;
;
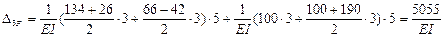
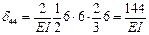 ,
,
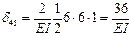 ;
;
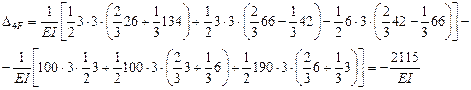
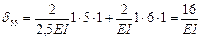
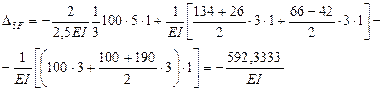
7. Подставляем эти значения в канонические уравнения, умножаем на жесткость 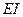 , переносим грузовые перемещения в правые части и решаем полученную систему уравнений методом уравнивания коэффициентов при неизвестных:
, переносим грузовые перемещения в правые части и решаем полученную систему уравнений методом уравнивания коэффициентов при неизвестных:
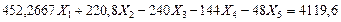
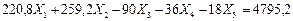
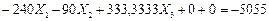 (7.26)
(7.26)
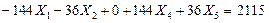
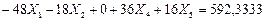
Уравниваем коэффициенты при неизвестном усилии 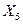 . Для этого первое уравнение делим на -48, второе уравнение делим на -18, четвертое и пятое уравнения делим соответственно на 36 и 16. Третье уравнение разделим на 333,3333. В результате получим систему уравнений (7.27):
. Для этого первое уравнение делим на -48, второе уравнение делим на -18, четвертое и пятое уравнения делим соответственно на 36 и 16. Третье уравнение разделим на 333,3333. В результате получим систему уравнений (7.27):
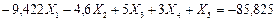
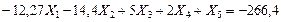
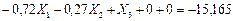 (7.27)
(7.27)
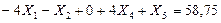
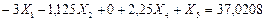
Вычитаем последовательно из первого уравнения системы (7.27) второе, четвертое и пятое уравнения и сохраняем третье уравнение без пятого слагаемого левой части, в результате получим:
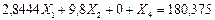
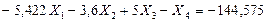
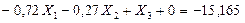 (7.28)
(7.28)
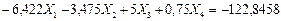
Исключаем в этой системе неизвестное усилие 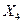 и получаем систему трех уравнений с тремя неизвестными:
и получаем систему трех уравнений с тремя неизвестными:
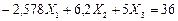
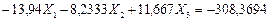 (7.29)
(7.29)
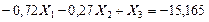
Уравниваем коэффициенты при неизвестном усилии 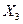 :
:
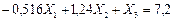
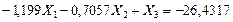 (7.30)
(7.30)
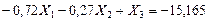
Вычитаем последовательно из первого уравнения второе и третье, получаем:
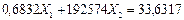
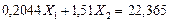 (7.31)
(7.31)
Уравниваем коэффициенты при неизвестном усилии 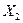 :
:
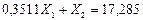
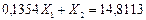 (7.32)
(7.32)
Вычитаем из первого уравнения второе, получаем:
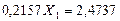 , откуда
, откуда 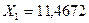 кН. Из первого уравнения системы (7.31) определяем величину усилия
кН. Из первого уравнения системы (7.31) определяем величину усилия 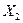 :
: 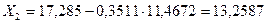 кН. Второе уравнение системы (7.31) используем для проверки выполненных вычислений:
кН. Второе уравнение системы (7.31) используем для проверки выполненных вычислений: 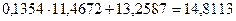 , откуда
, откуда 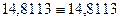 .
.
Из первого уравнения системы (7.30) определяем величину неизвестного усилия 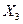 :
: 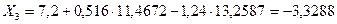 кН.
кН.
После подстановки величин трех найденных усилий во второе и третье уравнения системы (7.30) получаем тождественное равенство их левых и правых частей:
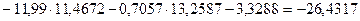 , откуда
, откуда 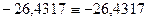 .
.
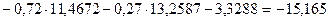 , откуда
, откуда 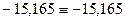 .
.
Величину неизвестного усилия 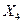 определяем из первого уравнения системы (7.28):
определяем из первого уравнения системы (7.28):
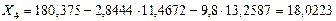 кН.
кН.
Остальные три уравнения системы (2.11) обращаются в тождества при подстановке значений найденных усилий.
Величину неизвестного усилия 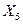 определяем из первого уравнения системы (7.27):
определяем из первого уравнения системы (7.27):
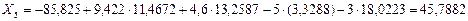 кНм.
кНм.
Остальные четыре уравнения системы (7.27) обращаются в тождества при подстановке значений найденных усилий.
8. Строим исправленные эпюры изгибающих моментов в основной системе. Для этого ординаты единичных эпюр умножаем на соответствующие значения найденных усилий с учетом их знаков. Если усилие имеет знак плюс, то исправленная эпюра совпадает по виду с единичной эпюрой, но имеет другие ординаты. Если же усилие имеет знак минус, то исправленная эпюра имеет зеркальное изображение
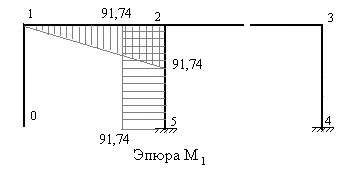
Рис.7.50
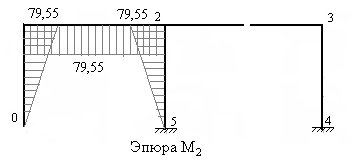
Рис.7.51
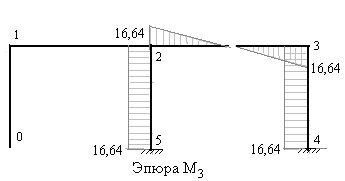
Рис.7.52
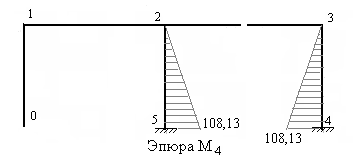
Рис.7.53
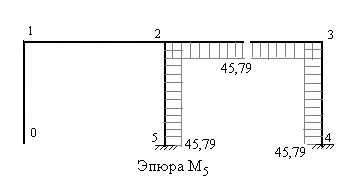
Рис.7.54
единичной эпюры, т.е. единичную эпюру необходимо повернуть вокруг оси каждого стержня на угол равный 1800 и её ординаты умножить на модуль усилия. В рассматриваемом примере ординаты исправленной эпюры М3 откладываем от оси каждого стержня, противоположно ординатам единичной эпюры. На рис.7.50 – 7.54 построены исправленные эпюры.
9. Строим эпюру изгибающих моментов в заданной статически неопределимой раме. Ордината эпюры изгибающих моментов в любом сечении заданной рамы равна алгебраической сумме ординат, взятых в том же сечении грузовой эпюры и всех исправленных эпюр. На рис 7.55 построена эпюра изгибающих моментов в заданной раме. Рекомендуем проверить правильность вычисления ординат этой эпюры в характерных сечениях каждого стержня заданной рамы, а также осуществить статическую и деформационную проверки, как было выполнено в примерах 1 и 2.
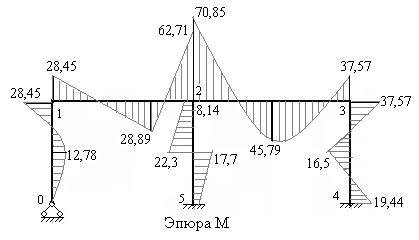
Рис.7.55
10. Вычисляем поперечные силы на отдельных участках рамы по формуле Журавского (на участках, где эпюра М прямолинейна) или по методу равновесия дисков (на участках, где эпюра М криволинейна). На рис.7.56 построена эпюра поперечных сил. Предлагаем проверить правильность вычисления ординат этой эпюры.
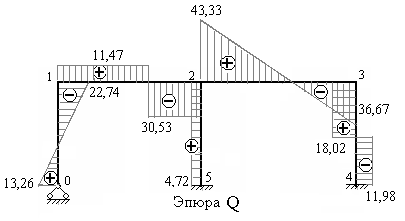
Рис.7.56
11. Вычисляем продольные силы в стержнях заданной рамы, пользуясь методом равновесия узлов, и строим эпюру N (рис.7.57).
Предлагаем проверить ординаты эпюры продольных сил и выполнить проверку равновесия рамы в целом, как было выполнено в примерах 1 и 2.
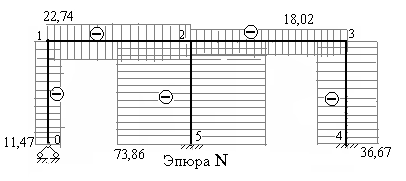
Рис.7.57
Вопросы для самоконтроля полученных знаний.
1. Какая система является статически неопределимой?
2. Как степень статической неопределимости связана с числом степеней свободы?
3. Какова степень статической неопределимости замкнутого бесшарнирного. контура?
4. Как определить степень статической неопределимости системы, исходя из понятия о замкнутом контуре?
5. Какие системы относят к внутренне статически неопределимым?
6. Назовите три основных метода расчета статически неопределимых систем.
7. Что принимается в качестве неизвестных метода сил?
8. Что представляет собой основная система метода сил?
9. В чем различие между абсолютно необходимыми и условно необходимыми связями?
10. Могут ли абсолютно необходимые связи считаться лишними?
11. Приведите возможные способы отбрасывания связей.
12. Что представляют собой канонические уравнения метода сил?
13. Что представляют собой коэффициенты и свободные члены канонических уравнений метода сил?
14. Какой метод положен в основу определения коэффициентов и свободных членов канонических уравнений?
15. Каково свойство главных коэффициентов канонических уравнений?
16. Как можно определить усилия в заданной системе после определения лишних неизвестных?
17. Как проверить правильность вычисления коэффициентов и свободных членов канонических уравнений?
18. Как проверить правильность расчета статически неопределимой системы методом сил?
19. Какие способы применяются для упрощения расчета симметричных систем методом сил?
20. Какие преимущества дает выбор симметричной системы метода сил при расчете на: а) произвольную нагрузку, б) симметричную и в) кососимметричную нагрузку?
21. Как определить перемещение в статически неопределимой системе?
Дата добавления: 2019-04-03; просмотров: 13094;
