Краткая характеристика статически неопределимых рам. Степень статической неопределимости.

Рамой называют систему, состоящую из прямолинейных стержней, объединенных между собой в узлах жестко или шарнирно и присоединенных к неподвижным телам при помощи опорных устройств. Плоские рамы могут иметь защемляющие, шарнирно неподвижные и шарнирно подвижные опоры. Вертикальные стержни рамы называют стойками, а горизонтальные - ригелями. В отдельных случаях рама может иметь наклонные стойки или наклонные ригели.

Если реакции опор рамы могут быть определены из уравнений равновесия статики, то рама является статически определимой.

Если же реакции опор рамы не могут быть определены из уравнений равновесия статики, то рама является статически неопределимой.

Разность между числом неизвестных усилий, возникающих в связях статически неопределимой рамы от действия заданных внешних нагрузок и числом уравнений равновесия, которые можно составить для этой рамы по методу равновесия дисков, называется степенью статической неопределимости рамы. Степень статической неопределимости обозначается буквой Ли выражает собой количество «лишних» связей статически неопределимой рамы, т.е. количество связей, для определения которых недостает уравнений равновесия.

Любая статически неопределимая плоская рама имеет определенное число дисков, объединенных между собой цилиндрическими шарнирами и прикрепленных к неподвижным телам с помощью опорных связей. Обозначим через Д - число простых дисков рамы (дисков, которые не содержат замкнутых контуров), через Ш_н - число простых цилиндрических шарниров (шарниров, которые объединяют между собой только два диска) и через С_о- число простых одиночных опорных связей заданной рамы (защемляющая опора плоской рамы имеет три простые связи, шарнирно неподвижная опора имеет две простые связи и шарнирно подвижная опора имеет одну простую связь).

Тогда степень статической неопределимости плоской рамы будет равна:

Л = 2Ш_н + С_о – 3Д (7.1)

Примечания: 1) Если цилиндрический шарнир объединяет в одной точке несколько дисков, то он является составным или кратным, т.е. эквивалентным нескольким простым шарнирам. Кратность составного шарнира равна количеству объединяемых дисков без одного, т.е.

К_ш = Д -1 (7.2)

2) Если диск содержат один замкнутый контур, то он являются три раза статически неопределимым. Рама может иметь несколько замкнутых контуров, тогда при определении степени статической неопределимости рамы необходимо в правой части формулы (7.1) прибавить утроенное число замкнутых контуров рамы Кили уменьшить число дисков на число замкнутых контуров. В этом случае степень статической неопределимости плоской рамы с замкнутыми контурами будет определяться по следующей формуле:

Л = 2Ш_н + С_о – 3(Д –К) (7.3)

3) Число простых одиночных опорных связей С_о определяется в зависимости от принятых типов опорных устройств рамы.

Рассмотрим три расчетные схемы статически неопределимых рам и установим их степень статической неопределимости.

Двухэтажная однопролетная рама 1 (рис.7.1,а) состоит из двух дисков (Д=2), двух простых цилиндрических шарниров (Ш_н=2) и пяти простых одиночных опорных связей (С_о=5). Применяя формулу (6.1) найдем:

Л = 2∙2 + 5 – 3∙2 = 3 , следовательно, рама 1 три раза статически неопределима, т.е. имеет три «лишние» связи.

Одноэтажная двухпролетная рама 2 (рис.7.1,б) состоит из трех дисков, двух простых цилиндрических шарниров (один двукратный шарнир) и 9 простых одиночных опорных связей (три защемляющие опоры). Тогда, по формуле (7.1) находим:

Л = 2∙2 + 9 – 3∙3 = 4, следовательно, рама 2 имеет четыре «лишние» связи, т.е. четыре раза статически неопределима.

Двухэтажная однопролетная рама 3 (рис.7.1,в) состоит из одного диска, имеющего один замкнутый контур, и пяти простых опорных связей. Тогда по формуле (7.3) найдем:

Л = 5 – 3(1-1) = 5, следовательно, рама 3 имеет пять «лишних» связей и является пять раз статически неопределимой..

Напомним, что для определения числа дисков необходимо отбросить мысленно все опорные и все шарнирные связи. Если, при этом, рама разделится (распадется) на отдельные части, то каждая из них будет являться отдельным диском. Если рама не делится на части, то она состоит из одного диска.

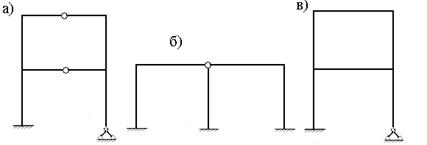
Рис.7.1

Любая связь рамы имеет две характеристики: статическую и кинематическую. Статическая характеристика определяет величину и направление реакции рассматриваемой связи, а кинематическая характеристика величину и направление перемещения, которое допускает данная связь.

Статическая и кинематическая характеристики связей находятся в определенной математической зависимости, устанавливаемой физическим законом деформирования упругих систем. Поэтому расчет рамы всегда состоит в определении статических и кинематических характеристик.

Если за независимые неизвестные принимают усилия в связях рамы, то метод расчета называют методом сил. Если же за независимые неизвестные принимают кинематические характеристики связей, то метод расчета называют методом перемещений.

В настоящей главе рассматривается метод сил, являющийся одним из основных методов расчета рам, а также других стержневых систем.

7.2. Основная система метода сил.

При использовании метода сил за неизвестные принимаются усилия в тех связях заданной рамы, которые приняты «лишними». За лишние связи могут приниматься любые связи рамы при условии, что после их освобождения полученная система будет статически определимой, геометрически неизменяемой и неподвижной. Такая система называется основной системой метода сил (ОС). Для любой статически неопределимой рамы можно образовать несколько вариантов основной системы. Чем выше степень статической неопределимости рамы, тем больше вариантов основной системы возможно образовать.

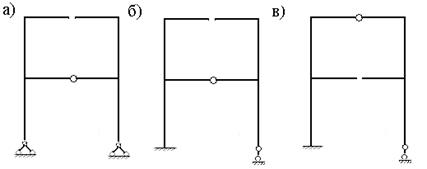
Рис.7.2

На рис.6.2 показаны три варианта основной системы метода сил, которые могут быть приняты при расчете рамы, представленной на рис.7.1,а. Они образуются освобождением трех связей заданной рамы.

Первый вариант ОС образуем путем удаления одного шарнира (удобнее шарнира второго этажа заданной рамы) и замены защемляющей опоры шарнирно неподвижной опорой (рис.7.2,а). Второй вариант ОС можно образовать путем удаления того же шарнира и замены правой шарнирно неподвижной опоры шарнирно подвижной опорой (рис.7.2,б). В третьем варианте ОС удаляем шарнир первого этажа и заменяем защемляющую опору шарнирно неподвижной опорой (рис.7.2,в).

Для расчета рамы можно использовать любой вариант основной системы, но удачный её выбор позволяет упростить решение задачи. Если удается образовать основную систему, имеющую геометрическую и жесткостную симметрии, то достигается упрощение уравнений относительно неизвестных метода сил. Этим условиям удовлетворяет первый вариант ОС и его следует пронять для расчета заданной рамы.

Для образования основной системы метода сил при расчете рамы (рис.7.1,б) необходимо удалить четыре связи.

В первом варианте можно освободить связи двукратного шарнира.

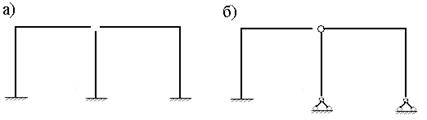
Рис.7.3

В результате ОС метода сил будет состоять из трех дисков с защемляющими опорами (оис.7.3,а). Во втором варианте освобождаем связи одного шарнира и заменяем две защемляющие опоры шарнирно неподвижными опорами (рис.7.3,б).

Для образования основной системы метода сил при расчете рамы (рис.7.1,в) необходимо удалить пять связей. Три из них освобождаем, рассекая один из ригелей рамы (лучше верхний), одну связь освобождаем введением шарнира в сечение другого ригеля, и одну связь освобождаем на одной из опор. В результате получаем три варианта ОС, представленные на рис.7.2.

7.3. Эквивалентная система метода сил.

Если основную систему метода сил загрузить заданными нагрузками и неизвестными усилиями в освобожденных связях, то полученная система будет называться эквивалентной системой (ЭС). Неизвестные усилия в освобожденных связях обозначают буквой 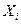независимо от того, является ли неизвестное усилие сосредоточенной силой или сосредоточенным моментом. Индекс усилия обозначает порядковый номер освобожденной связи.

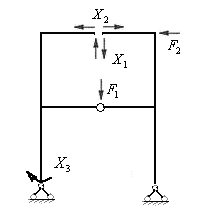
Рис.7.4

Образуем эквивалентную систему для рамы (рис.7.1,а), приняв для расчета первый вариант основной системы. Для этого загрузим ОС заданными нагрузками (например, двумя сосредоточенными силами 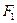и ) и 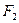тремя неизвестными усилиями, компенсирующими влияние удаленных связей заданной рамы. Усилия 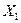и 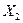, которые удаленный шарнир передает от одного диска к другому, прикладываем к разъединенным концам ригеля. Вертикальные силы 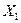являются поперечными силами в ригеле. Они равны по величине и противоположны по направлению. Горизонтальные силы 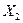являются продольными силами в ригеле и также равны по величине и противоположны по направлению. Усилие 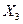, компенсирующее влияние освобожденной опорной связи, которая препятствовала повороту опорного сечения левой стойки рамы, является реактивным моментом. Его направляем по ходу часовой стрелки (или против часовой стрелки). В результате получаем эквивалентную систему, показанную на рис.7.4

В эквивалентной системе под действием всех нагрузок могут возникать перемещения по направлению реакций удаленных опор или взаимные перемещения разъединенных точек отдельных стержней, в которых освобождены внутренние связи рамы, по направлению их реакций. При некоторых определенных значениях неизвестных усилий в освобожденных связях, зависящих от характера и величины внешнего загружения рамы, а также от геометрических размеров стержней и величин их изгибных жесткостей, указанные перемещения обращаются в нуль.

Условия равенства нулю перемещений точек эквивалентной системы по направлению неизвестных усилий, компенсирующих влияние освобожденных связей заданной рамы, называются условиями эквивалентности или условиями неразрывности перемещений в точках, где освобождены связи. Число условий эквивалентности всегда равно степени статической неопределимости рамы или числу неизвестных сил сопротивления, компенсирующих влияние освобожденных связей заданной рамы. Для ЭС показанной на рис.7.4 должны выполняться три условия эквивалентности:

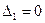
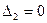(7.4)

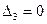
7.4. Канонические уравнения метода сил.

Канонические уравнения метода сил вытекают из условий эквивалентности (7.4) при использовании принципа независимости действия нагрузок, приложенных к эквивалентной системе (ЭС).

Составим первое каноническое уравнение, используя условие эквивалентности 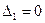системы (рис.7.4).

Под действием всех нагрузок, приложенных к эквивалентной системе, точки приложения сил 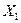могут получить взаимное смещение в вертикальном направлении на величину 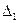. Используя принцип независимости действия нагрузок, найдем:

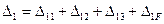(7.5)

Т.е. взаимное перемещение по направлению сил 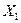в эквивалентной системе (из рисунка 7.4 следует, что это взаимное вертикальное перемещение) равно сумме взаимных перемещений по направлению силы 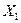, вызванных действием всех неизвестных усилий 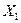, , 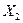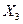и всех заданных внешних нагрузок. Перемещение по направлению любого неизвестного усилия не равного единице, равно произведению модуля этого усилия на единичное перемещение, т.е.

, ,

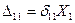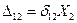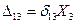
Подставим эти значения в равенство (7,5 ) и приравняем к нулю 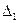, в результате получим первое каноническое уравнение метода сил для рамы с тремя лишними связями.

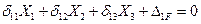
Используя аналогично два последующих условия эквивалентности (7.4), получим второе и третье канонические уравнения метода сил. Все три уравнения составляют систему канонических уравнений метода сил.

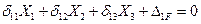
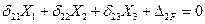(7.6)

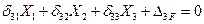
Любое каноническое уравнение метода сил является отрицанием наличия перемещения по направлению соответствующего неизвестного усилия в эквивалентной системе. В этом состоит физический смысл канонических уравнений метода сил.

В общем случае, когда заданная рама имеет n «лишних» связей, система канонических уравнений метода сил имеет вид:

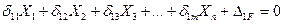
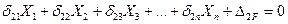
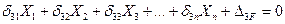(7.7)

.……………………………………………

……………………………………………

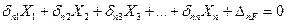
7.5. Анализ коэффициентов и свободных членов канонические уравнения метода сил.

Коэффициенты канонических уравнений метода сил являются единичными перемещениями точек основной системы (ОС), где освобождены связи. Они возникают по направлению неизвестного усилия, индекс которого совпадает с первым индексом перемещения, от действия единичного значения неизвестного усилия, индекс которого совпадает со вторым индексом искомого перемещения. Так, например, коэффициент δ_ik есть единичное перемещение в основной системе по направлению усилия X_i от действия усилия X_k=1.

Свободные члены канонических уравнений являются грузовыми перемещениями в основной системе по направлению неизвестных усилий, индексы которых совпадают с первыми индексами искомых перемещений.

Все коэффициенты канонических уравнений метода сил делятся на две группы: главные и побочные. Главные коэффициенты имеют одинаковые индексы и всегда имеют положительные значения. Они расположены по главной диагонали канонических уравнений (7.6) или (7.7).

Побочные коэффициенты имеют разные индексы и могут быть положительными, отрицательными или равными нулю. При этом побочные коэффициенты, расположенные симметрично главной диагонали обладают свойством взаимности, т.е. равны по величине и знаку на основании теоремы о взаимности возможных перемещений. Например, 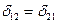, 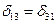и т.д. Это свойство позволяет сократить количество коэффициентов, подлежащих определению. Например, система уравнений (7.6) девять неизвестных коэффициентов: три главных и шесть побочных. Вычислению подлежат главные коэффициенты и половина побочных, т.е. три. Всего необходимо вычислить шесть коэффициентов и три грузовые перемещения.

7.6. Способы вычисления коэффициентов и свободных членов канонические уравнения метода сил.

Все известные способы (методы) определения упругих перемещений могут быть использованы для вычисления коэффициентов и грузовых перемещений канонических уравнений метода сил. Основными из них являются: метод начальных параметров, метод упругих грузов, метод Мора-Максвелла, правило Верещагина.

Остановимся подробнее на использовании двух последних методов.

Метод Мора-Максвелла состоит в использовании универсальной формулы упругих перемещений стержневых систем. Например, при расчете балочных и рамных статически неопределимых стержневых систем, коэффициенты и грузовые перемещения вычисляются по формулам:

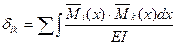(7.8)

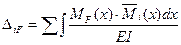(7.9)

В этих формулах содержаться уравнения изгибающих моментов на каждом участке основной системы:

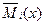- уравнение изгибающих моментов на произвольном участке основной системы, загруженной силой ;

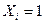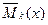- уравнение изгибающих моментов на том же участке основной системы, загруженной силой ;

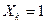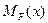- уравнение изгибающих моментов на том же участке основной системы, загруженной всеми внешними нагрузками.

При расчете статически неопределимых рам рекомендуется вычислять коэффициенты и грузовые перемещения по правилу Верещагина путем перемножения эпюр изгибающих моментов, построенных в основной системе метода сил.

Для этого необходимо построить единичные и грузовую эпюры изгибающих моментов в основной системе. Если загрузить основную систему силой 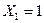, определить реакции опор, вычислить изгибающие моменты на концах каждого стержня, отложить их от оси стержня в сторону растянутой зоны и соединить прямыми линиями, то получим единичную эпюру .

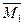При вычислении изгибающих моментов в характерных сечениях стержней рамы необходимо придерживаться следующего порядка их рассмотрения:

- сначала рассматривают стержни от опор, реакции которых вычислены, к жестким узлам рамы;

- затем рассматривают консольные части стержней от их свободных концов к жестким узлам рамы;

- стержни рамы, объединяющие жесткие узлы, рассматривают в последнюю очередь.

При этом каждый жесткий узел рамы должен находиться в равновесии под действием узловых изгибающих моментов. Это свойство используется как для проверки правильности построения эпюр, так и для определения изгибающего момента в узловом сечении одного из стержней, если изгибающие моменты в узловых сечениях остальных стержней уже известны.

Аналогично осуществляют построение единичных эпюр изгибающих моментов 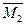, 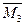и

Для построения грузовой эпюры изгибающих моментов 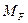в основной системе метода сил следует загрузить эту систему заданными нагрузками, определить реакции опор, разделить раму на участки и вычислить изгибающие моменты на концах каждого из них. Если участок загружен распределенной нагрузкой, то необходимо дополнительно вычислить изгибающий момент посредине этого участка.

После построения единичных и грузовой эпюр изгибающих моментов в основной системе, вычисляют по правилу Верещагина коэффициенты и грузовые перемещения по формулам:

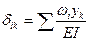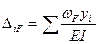, (7.10)

Где: ω_i – площадь эпюры 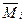на произвольном участке;

ω_F - площадь эпюры 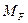на произвольном участке;

y_i - ордината эпюры 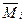, взятая под центром тяжести эпюры ;

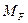y_k - ордината эпюры 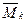, взятая под центром тяжести эпюры .

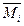Учитывая, что единичные эпюры изгибающих моментов на каждом участке основной системы прямолинейные и чаще всего имеют форму треугольника или прямоугольника, коэффициенты канонических уравнений легко вычисляются. Грузовая эпюра изгибающих моментов может иметь криволинейное очертание на отдельных участках, которые несут распределенную нагрузку. Такая эпюра всегда может быть разделена на составные части, площади и положения центров тяжести которых, легко определяются.

Таким образом, всегда есть возможность вычислить единичные и грузовые перемещения по формулам (7.10).

7.7. Способы решения канонические уравнения метода сил.

Канонические уравнения метода сил являются линейными алгебраическими уравнениями с постоянными коэффициентами.

Решение системы канонических уравнений метода сил (7.6) или (7.7) можно получить методом последовательного исключения неизвестных (уравнивания коэффициентов при неизвестных), либо методом определителей (детерминантов).

При использовании первого метода каждое уравнение делят на коэффициент при одном из неизвестных усилий (например, на коэффициент при неизвестной силе 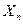), т.е. уравнивают коэффициенты при неизвестной силе 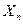в каждом уравнении. Вычитая, затем, из первого уравнения второе, из второго уравнения третье и т.д., получаем новую систему уравнений, не содержащую неизвестной силы 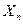. Число уравнений новой системы будет на одно меньше числа уравнений исходной системы.

Аналогично исключают из уравнений неизвестные 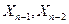и так далее, пока не получим одно уравнение с одной неизвестной 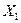. Вычислив значение 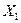, вычисляют последовательно, обратным ходом, значения 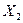, 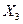и т.д.

При этом рекомендуется осуществлять поэтапную проверку найденных значений искомых усилий. Усилие определяется из одного уравнения системы, а левые части остальных уравнений должны быть равными нулю при подстановке вычисленных усилий.

При использовании второго метода любое неизвестное усилие определяется отношением определителя неизвестного к определителю системы уравнений, т.е. по формуле:

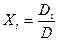(7.11)

Определитель системы формируется из коэффициентов системы канонических уравнений. Число строк и число столбцов этого определителя равно числу канонических уравнений. При n неизвестных метода сил он имеет следующий вид:

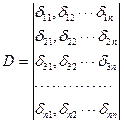(7.12)

Определитель неизвестного формируется из определителя системы уравнений путем замены в нем столбца коэффициентов при определяемом неизвестном усилии свободными членами канонических уравнений, перенесенными в их правые части.

Например, определитель неизвестного усилия 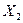имеет вид:

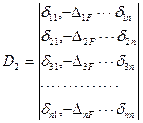(7.13)

Метод определителей позволяет вычислить неизвестные усилия метода сил с использованием функции «МОПРЕД» программы Microsoft Excel. Для этого достаточно сформировать определитель системы и определители каждого неизвестного, применить указанную функцию и найти отношения матриц определителей по формуле (7.11).