Вычисление перемещений перемножением эпюр изгибающих моментов (правило Верещагина).

Обозначим букой 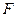заданное состояние стержневой системы и буквой 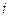возможное единичное состояние той же системы. Тогда вычисление упругих перемещений по формуле Мора будет связано с вычислением интеграла:

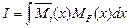(6.22)

Рассмотрим случай, когда эпюра изгибающих моментов на некотором участке заданного состояния имеет произвольное очертание (не прямолинейна), а единичная эпюра изгибающих моментов на том же участке возможного состояния прямолинейна (рис.6.8).

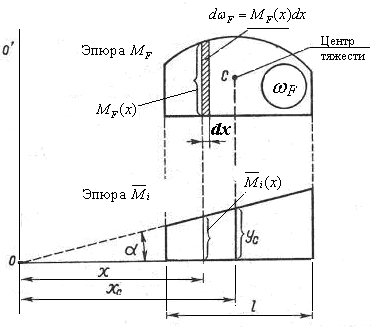
Рис.6.8

Выделим элементарную полоску эпюры 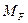шириной 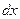, тогда её площадь будет равна .

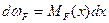Ордината единичной эпюры изгибающих моментов под полоской равна 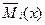. Выразим эту ординату через угол наклона эпюры к горизонтальной прямой:

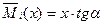, тогда интеграл (6.22) преобразуется к виду:

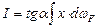(6.23)

Легко заметить, что интеграл выражения (6.23) равен статическому моменту площади эпюры 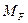относительно вертикальной оси, проходящей через точку О. Из теоретической механики известно, что статический момент площади относительно оси равен произведению этой площади на расстояние от её центра тяжести до оси.

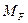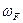Обозначим площадь эпюры через , а расстояние от её центра тяжести до оси, через 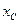, тогда получим:

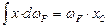(6.24)

В результате интеграл (6.23) преобразуется к виду:

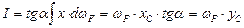(6.25)

Таким образом, интеграл (6.22) на любом участке, где одна из двух эпюр изгибающих моментов прямолинейная, равен произведению площади не прямолинейной эпюры на ординату прямолинейной эпюры, взятую под центром тяжести первой.

Для стержневой системы, имеющей несколько участков, упругое перемещение определяется по формуле:

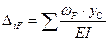(6.26)

Правило знаков: Если перемножаемые эпюры изгибающих моментов в двух состояниях расположены по одну сторону от осей системы, то результат перемножения имеет знак плюс. Если же перемножаемые эпюры расположены по разные стороны от осей системы, то результат перемножения имеет знак минус.

Примечания: 1) Перемещение, вычисленное по правилу Верещагина (по формуле 6.26) может иметь знак плюс или минус. Направление перемещения определяется направлением единичной силы возможного состояния. Следовательно, если перемещение имеет знак плюс, то оно имеет то же направление, что и единичная сила. Если же перемещение имеет знак минус, то оно направлено противоположно единичной силе.

2) При перемножении двух прямолинейных эпюр можно вычислять площади любой из них на отдельных участках, а ординаты под их центрами тяжести принимать из другой эпюры.

Пример 6.2Определить прогиб по середине пролета балки постоянной жесткости 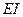, загруженной равномерно распределенной нагрузкой (рис.6.9).

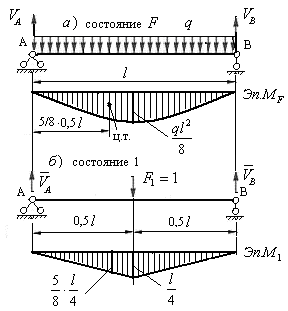
Рис.6.9

Решение: 1) Заданную состояние балки обозначим 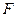, вычислим реакции опор, составим уравнение изгибающих моментов в произвольном сечении и построим эпюру изгибающих моментов :

,

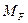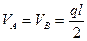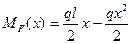
Эпюра 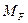ограничена квадратичной параболой, имеющей нулевые ординаты под опорами и максимальную ординату по середине пролета балки. Эта ордината равна:

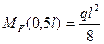
2) Создаем возможное состояние 1 путем загружения той же балки одной единичной сосредоточенной силой 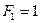, вычисляем реакции опор и строим единичную эпюру изгибающих моментов 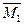. 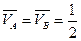(направления реакций показаны на рис.6.9,б),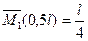

3) Вычисляем прогиб балки в направлении силы 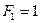, перемножая эпюры изгибающих моментов в двух состояниях по правилу Верещагина. Эпюра 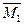прямолинейна на двух участках балки, симметричных относительно середины пролета. На тех же участках эпюра 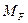криволинейна и симметрична. Поэтому перемножаем эпюры на левом участке и результат удваиваем., т.е.:

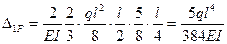
Примечание: Площадь выпуклого параболического сегмента равна 2/3 произведения высоты на длину, центр тяжести отстоит от нулевой вершины на расстоянии 5/8 длины участка.

Вопросы для самоконтроля полученных знаний.

1. Для каких целей необходимо вычислять перемещения?

2. Как формулируется принцип возможных перемещений для упругих систем?

3. Что такое возможное перемещение?

4. Как зависят перемещения от нагрузки в линейно деформируемых системах?

5. Как определяется действительная работа внешних сил?

6. В чем различие между действительной и возможной работой?

7. Как определяется возможная работа внутренних сил?

8. Чем объясняется наличие знака «минус» в выражении возможной работы внутренних сил?

9. Как получить действительную работу внутренних сил?

10. Как определяется потенциальная энергия деформации системы?

11. Как зависит потенциальная энергия от нагрузки? От перемещений?

12. Каковы свойства потенциальной энергии?

13. Как формулируется и доказывается теорема Бетти о взаимности работ?

14. Сформулируйте и докажите теорему Максвелла о взаимности перемещений; теорему о взаимности реакций; теорему о взаимности перемещений и реакций.

15. Как записывается формула Мора?

16. Какие два состояния системы необходимо рассматривать при определении перемещений по формуле Мора?

17. Когда можно применять правило Верещагина? Формулу Симпсона?