Вычисление лагранжевых коэффициентов

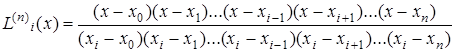(5.2)

Можно записать лагранжевы коэффициенты и более компактно: 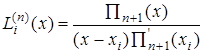, (5.3)

где .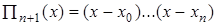

Формула Лагранжа при этом имеет вид .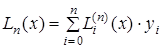

Для вычисления лагранжевых коэффициентов может быть использована приведенная ниже схема. Сначала располагаем в таблицу разности

Таблица 5.3.

Таблица разностей

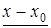
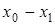
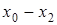
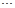
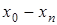
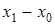
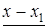
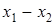
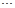
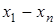
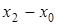
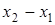
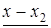
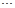
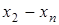
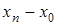
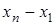
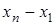
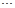
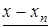
Обозначим произведение элементов первой строки через D0, второй – D1и т.д. Произведение же элементов главной диагонали, очевидно, будет 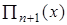. Отсюда следует, что

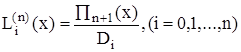.Следовательно,

.

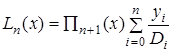Пример 5.3 Выполнено в Mathcad

Найти приближенное значение функции при данном значении аргумента с помощью интерполяционного многочлена Лангранжа, если функция задана в неравно- отстоящих узлах таблицы.

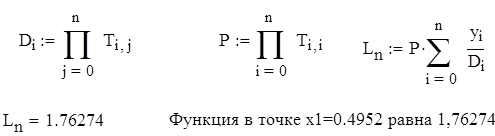
Рис 5.2. Решения примера 5.3 в Mathcad

Отметим, что форма лагранжевых коэффициентов инвариантна относительно целой линейной подстановки 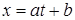(a,b – постоянны ). Действительно, положив в формуле (5.2):

, , ,

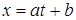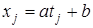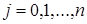после подстановки и сокращения числителя и знаменателя на aⁿ, получим:

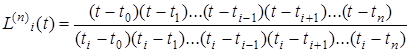
или

,

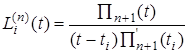где 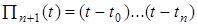, что и требовалось доказать.

В случае равноотстоящих точек лагранжевы коэффициенты могут быть приведены к более простому виду.

В самом деле, полагая 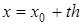, будем иметь: 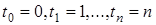. Отсюда

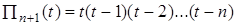и

.

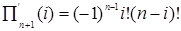Тогда ,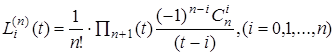

где 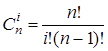. Отсюда можно записать:

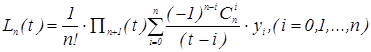(5.4)

где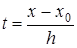

Пример 5.4 Выполно в Mathcad.

Найти приближенное значение функции при данном значении аргумента с помощью интерполяционного многочлена Лагранжа, если функция задана в равноотстоящих узлах таблицы

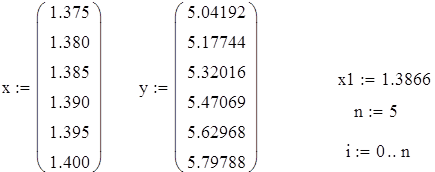
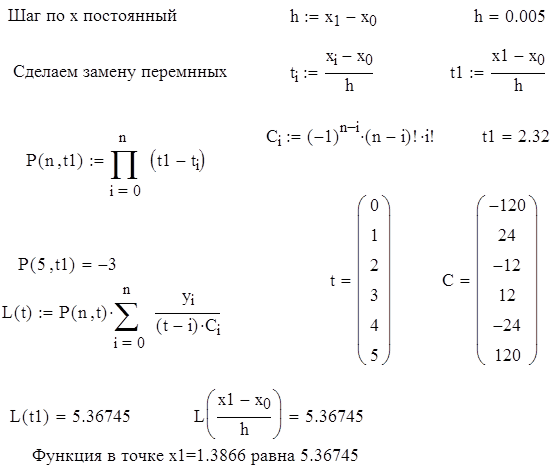
Рис 5.3. Решения примера 5.4 в Mathcad

Схема Эйткина

Пусть требуется найти не общее выражение 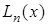, а лишь его значения при конкретных x. При этом, значения функции даны в достаточно большом количестве узлов, тогда удобно пользоваться интерполяционной схемой Эйткина. Согласно этой схеме последовательно вычисляются многочлены:

.

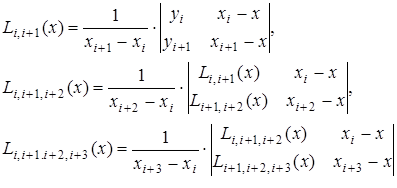Интерполяционный многочлен степени «n», принимающий в точках xiзначения 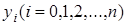, запишется следующим образом:

.

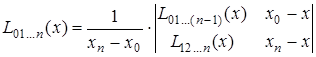Вычисления по схеме Эйткина удобно расположить в такой таблице:

Таблица 5.4.

Вычисления по схеме Эйткина

						…
						…

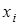
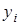
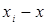
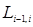
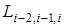
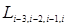
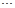
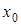
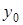
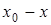
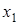
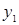
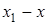
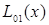
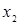
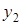
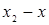
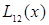
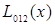
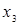
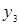
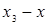
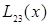
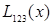
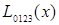
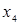
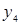
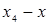
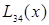
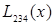
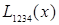
Вычисления по схеме Эйткина обычно ведут до тех пор, пока последовательные многочлены 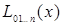и 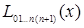в таблице 5.4 не совпадут в пределах заданной точности.

Пример 5.5 Функция 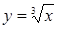задана таблицей

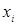
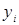
1.0	1.000
1.1	1.032
1.3	1.091
1.5	1.145
1.6	1.170

Применяя схему Эйткина, найти 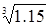Составим таблицу 5.4 для примера:

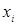
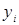
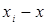
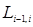
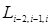
1.0	1.000	-0.15
1.1	1.032	-0.05	1.048
1.3	1.091	0.15	1.047	1.048
1.5	1.145	0.35	1.050
1.6	1.170	0.45	1.057

Значения 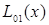и 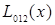совпадают до третьего знака. На этом вычисления можно прекратить и с точностью до 0.001 записать 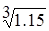=1.048