Остаточный член формулы Лагранжа
Остаточный член равен: 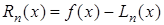 .
.
Для него справедлива следующая оценка:
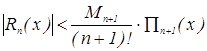 ,
,
где 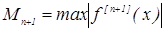 на отрезке
на отрезке 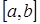 .
.
Обратное интерполирование
Пусть функция y = f(x) задана таблицей.
В задаче обратного интерполирования заключается в том, чтобы по заданному значению функции y определить соответствующее значение аргумента x. Мы будем считать, что в рассматриваемом интервале функция f(x) монотонна, так что поставленная задача имеет единственное решение. В этом случае задача решается с помощью интерполяционного многочлена Лагранжа. Для этого достаточно принять переменную y за независимую, а x считать функцией от y. Запишем по заданным узлам (yi, xi) (i = 0,1, … , n) многочлен Лагранжа
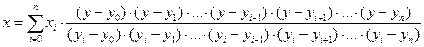
и определим x по заданному y. Остаточный член в этом случае можно получить из остаточного члена формулы Лагранжа, меняя местами x и y.
Пример 5.6. Функция y = f(x) задана таблицей
| x | ||||
| y |
Найти значение x, для которого y=10.
Интерполяционный многочлен Лагранжа имеет вид
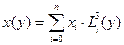
где 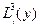 лагранжевы коэффициенты.
лагранжевы коэффициенты.
При y=10 получаем
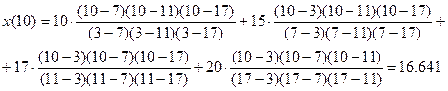
Дата добавления: 2017-05-18; просмотров: 1024;
