Квадратурные формулы Ньютона-Котеса
Рассмотрим применение в качестве 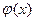 интерполяционного полинома Лагранжа.
интерполяционного полинома Лагранжа.
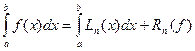 , (8.1)
, (8.1)
где 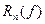 - ошибка квадратурной формулы (8.1) или остаточный член
- ошибка квадратурной формулы (8.1) или остаточный член
Выбрав шаг 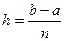 ,разобьем отрезок с помощью равноотстоящих точек
,разобьем отрезок с помощью равноотстоящих точек 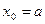 ,
, 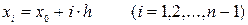 ,
, 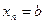 на n равных частей, и пусть
на n равных частей, и пусть 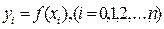 . Заменяя функцию соответствующим интерполирующим полиномом Лагранжа
. Заменяя функцию соответствующим интерполирующим полиномом Лагранжа
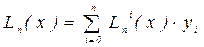 ,
,
получим приближенную квадратурную формулу:
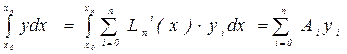 , (8.2)
, (8.2)
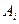 - некоторые постоянные коэффициенты. Найдём явные выражения для коэффициентов
- некоторые постоянные коэффициенты. Найдём явные выражения для коэффициентов 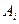 формулы (8.2).
формулы (8.2).
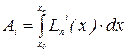
Коэффициенты полинома Лагранжа имеют вид:
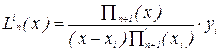 ,
,
где 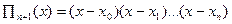 , причем
, причем 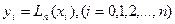 .
.
Введем обозначения: 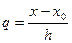 и
и 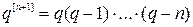 тогда
тогда
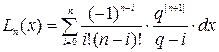 ,
,
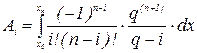 .
.
Сделав замену переменных в определенном интеграле 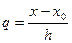 ,
, 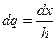 будем иметь:
будем иметь: 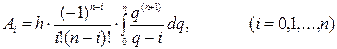 .
.
Учитывая, что 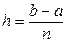 , обычно полагают
, обычно полагают 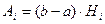 , где
, где 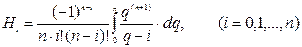 это постоянные, называемые коэффициентами Котеса.
это постоянные, называемые коэффициентами Котеса.
Квадратурная формула (8.2) принимает вид:
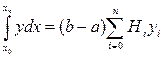 (8.3)
(8.3)
Формулы называются квадратурными формулами Ньютона-Котеса
Справедливы соотношения: 1. 
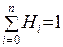 ; 2.
; 2. 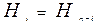 .
.
Формула трапеций и ее остаточный член
При n=1 получим
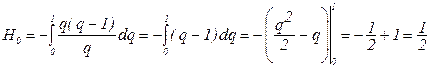 ,
, 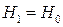 отсюда:
отсюда:
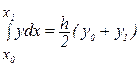 (8.4)
(8.4)
Если подынтегральная функция 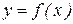 дважды дифференцируема, то остаточный член квадратурной формулы (8.4) равен:
дважды дифференцируема, то остаточный член квадратурной формулы (8.4) равен:
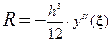 , где
, где 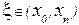
Дата добавления: 2017-05-18; просмотров: 626;
