Квадратурная формула Чебышева
Рассмотрим квадратурную формулу
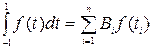 , (8.10)
, (8.10)
где 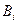 - постоянные коэффициенты. Чебышев предположил выбрать абсциссы
- постоянные коэффициенты. Чебышев предположил выбрать абсциссы 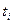 таким образом, чтобы:
таким образом, чтобы:
1. коэффициенты 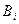 были равны между собой;
были равны между собой;
2. квадратурная формула (8.10) являлась точной для всех полиномов до степени n включительно.
Покажем, как могут быть найдены в этом случае величины 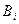 и
и 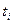 . Полагаем
. Полагаем 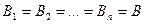 . Учитывая, что при
. Учитывая, что при 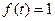 , будем иметь
, будем иметь 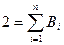 , получаем
, получаем 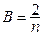 . Следовательно, квадратурная формула Чебышева имеет вид:
. Следовательно, квадратурная формула Чебышева имеет вид:
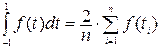 . (8.11)
. (8.11)
Для определения абсцисс 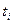 заметим, что формула (8.11) согласно условию 2 должна быть точной для функции вида
заметим, что формула (8.11) согласно условию 2 должна быть точной для функции вида 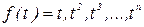 . Подставляя эти функции в формулу (8.11), получим систему уравнений:
. Подставляя эти функции в формулу (8.11), получим систему уравнений:
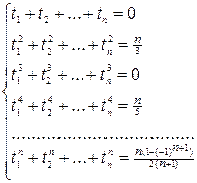 , (8.12)
, (8.12)
из которой могут быть определены неизвестные 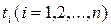 . Заметим, что система (8.12) при n=8 и n³10 не имеет действительных решений.
. Заметим, что система (8.12) при n=8 и n³10 не имеет действительных решений.
Выведем формулу Чебышева с тремя ординатами (n=3).
Для определения абсцисс 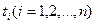 имеем систему уравнений:
имеем систему уравнений:
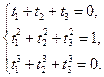 (8.13)
(8.13)
Рассмотрим симметрические функции корней: 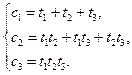
Из системы (8.13) имеем: 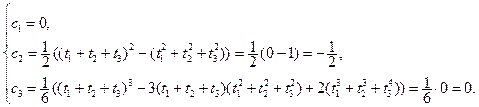
Отсюда заключаем по теореме Виета, что 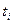 есть корни вспомогательного уравнения
есть корни вспомогательного уравнения 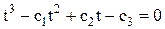 или
или 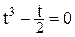 . Следовательно, можно принять:
. Следовательно, можно принять: 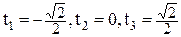 .
.
Таким образом, соответствующая формула Чебышева имеет вид 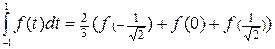 .
.
Чтобы применить квадратурную формулу Чебышева к интегралу вида 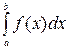 , следует преобразовать его с помощью подстановки:
, следует преобразовать его с помощью подстановки:
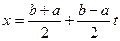 , переводящей отрезок
, переводящей отрезок 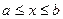 в отрезок
в отрезок 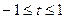 . Применяя к преобразованному интегралу формулу Чебышева, будем иметь
. Применяя к преобразованному интегралу формулу Чебышева, будем иметь
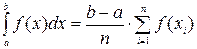 ,
,
где 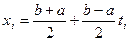 и
и 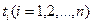 - корни системы (8.13).
- корни системы (8.13).
В таблице приведены значения корней ti системы (8.12) для n=1,2…,7.
Таблица 8.1
Значения абсцисс ti в формуле Чебышева
| n | i | ti |
| 2;1 | ±0.577350 | |
| 3;1 | ±0.707107 | |
| 4;1 3;2 | ±0.794654 ±0.187592 | |
| 5;1 4;2 | ±0.832498 ±0.374541 | |
| 6;1 5;2 4;3 | ±0.866247 ±0.422519 ±0.266635 | |
| 7;1 6;2 5;3 | ±0.883862 ±0.529657 ±0.323912 |
Пример 8.3. Вычислить интеграл из предыдущего примера по формуле Чебышева для четырех и для пяти точек в Mathcad.
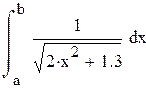
|
Оценить точность вычислений.
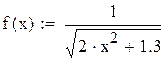
|
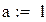
|
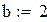
|
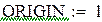
|
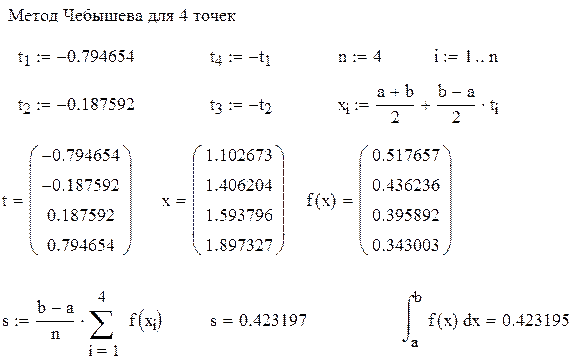
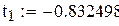
|
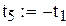
|
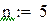
|
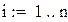
|
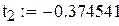
|
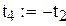
|
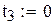
|
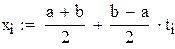
|
Вычисление интеграла методом Чебышева для 5точек
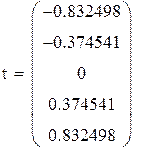
|
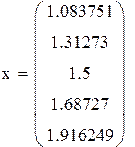
|
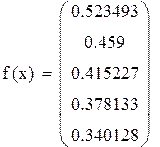
|
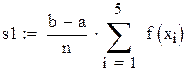
|
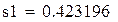
|
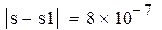
|
Рис. 8.3. Решение примера 8.2 в Mathcad
Дата добавления: 2017-05-18; просмотров: 810;
