Дивергенция, её физический смысл и свойства. Формула Остроградского-Гаусса
Пусть векторное поле 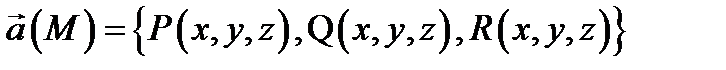 таково, что существуют частные производные
таково, что существуют частные производные 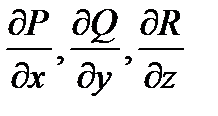 в точке
в точке 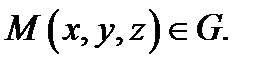
Определение 5.Дивергенцией поля 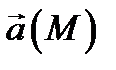 в точке
в точке 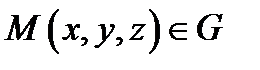 назывется скалярная величина
назывется скалярная величина 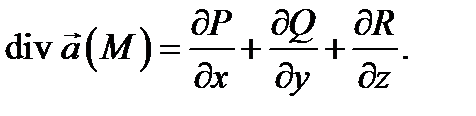 Если
Если 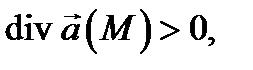 то точка
то точка 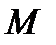 называется источником, а если
называется источником, а если 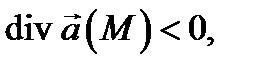 то
то 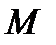 называется стоком.
называется стоком.
Это определение дивергенции дано в декартовой системе координат. Инвариантное определение будет дано позже. Дивергенция обладает следующими свойствами:
1 (Линейность). 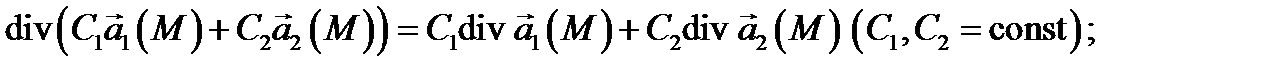
2. Если 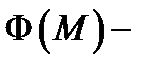 дифференцируемое в точке
дифференцируемое в точке 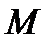 скалярное поле, а
скалярное поле, а 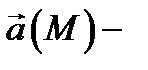 дифференцируемое в той же точке векторное поле, то в указанной точке
дифференцируемое в той же точке векторное поле, то в указанной точке 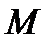 имеет место равенство
имеет место равенство
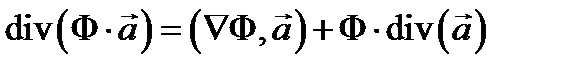 .
.
Доказательства этих свойств очевидны и мы рекомендуем провести их самостоятельно. Приводимая ниже формула Остроградского-Гаусса позволяет свести поверхностный интеграл второго рода (поток) к тройному интегралу. Введём сначала следующее понятие.
Определение 6.Говорят, что область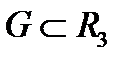 односвязна, если любой замкнутый контур
односвязна, если любой замкнутый контур 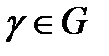 можно стянуть в точку, не выходя за пределы области
можно стянуть в точку, не выходя за пределы области 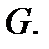
Например, шар – односвязная область, а шаровое кольцо – нет.
Теорема Остроградского-Гаусса.Пусть 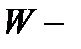 замкнутая ограниченная односвязная область и
замкнутая ограниченная односвязная область и 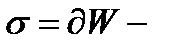 её граница ( в этом случае
её граница ( в этом случае 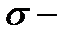 замкнутая поверхность). Пусть, кроме того, векторное поле
замкнутая поверхность). Пусть, кроме того, векторное поле 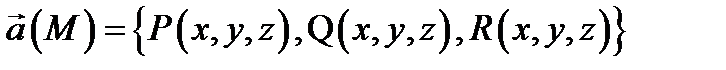 непрерывно дифференцируемо в
непрерывно дифференцируемо в 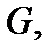 а граница
а граница  кусочно гладка. Тогда имеет место равенство
кусочно гладка. Тогда имеет место равенство
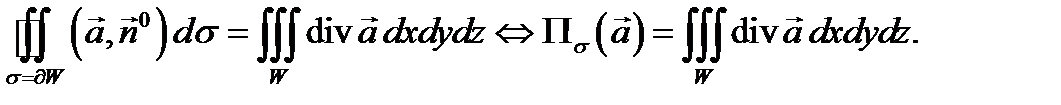
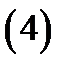
Доказательствопроведем для случая, когда тело 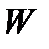 можно одновременно представить в следующих видах
можно одновременно представить в следующих видах
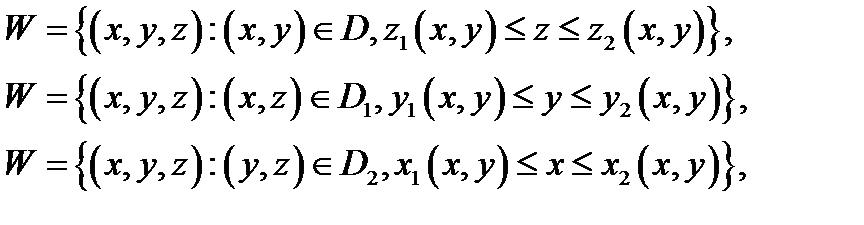
где
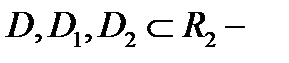 замкнутые ограниченные квадрируемые области, а все участвующие здесь функции
замкнутые ограниченные квадрируемые области, а все участвующие здесь функции 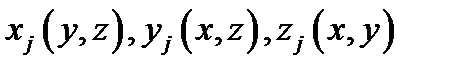 непрерывны в областях
непрерывны в областях 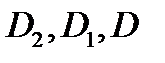 соответственно. Введем векторные поля
соответственно. Введем векторные поля 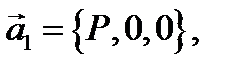
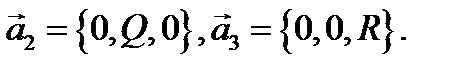 Тогда исходное векторное поле запишется в виде
Тогда исходное векторное поле запишется в виде 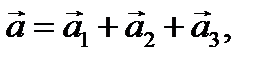 и значит,
и значит,
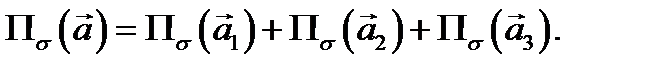
Подсчитаем каждый из этих потоков. Начнем с потока 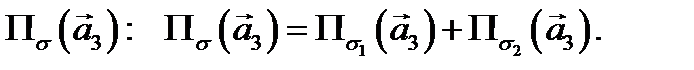
Нормаль 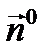 на поверхности
на поверхности 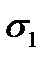 имеет вид
имеет вид 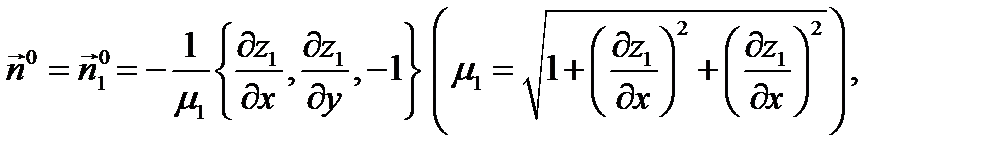 так как угол
так как угол 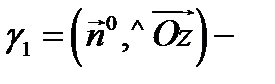 острый,
острый,
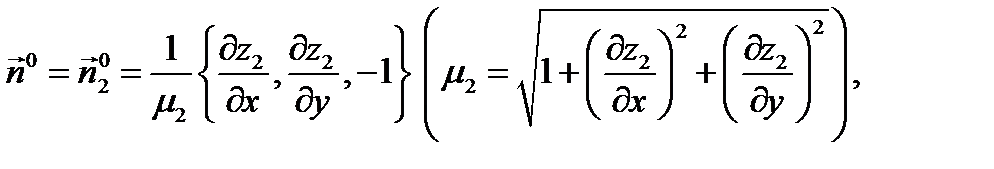 так как угол
так как угол 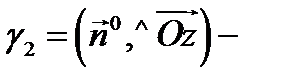 тупой.
тупой.
Следовательно,
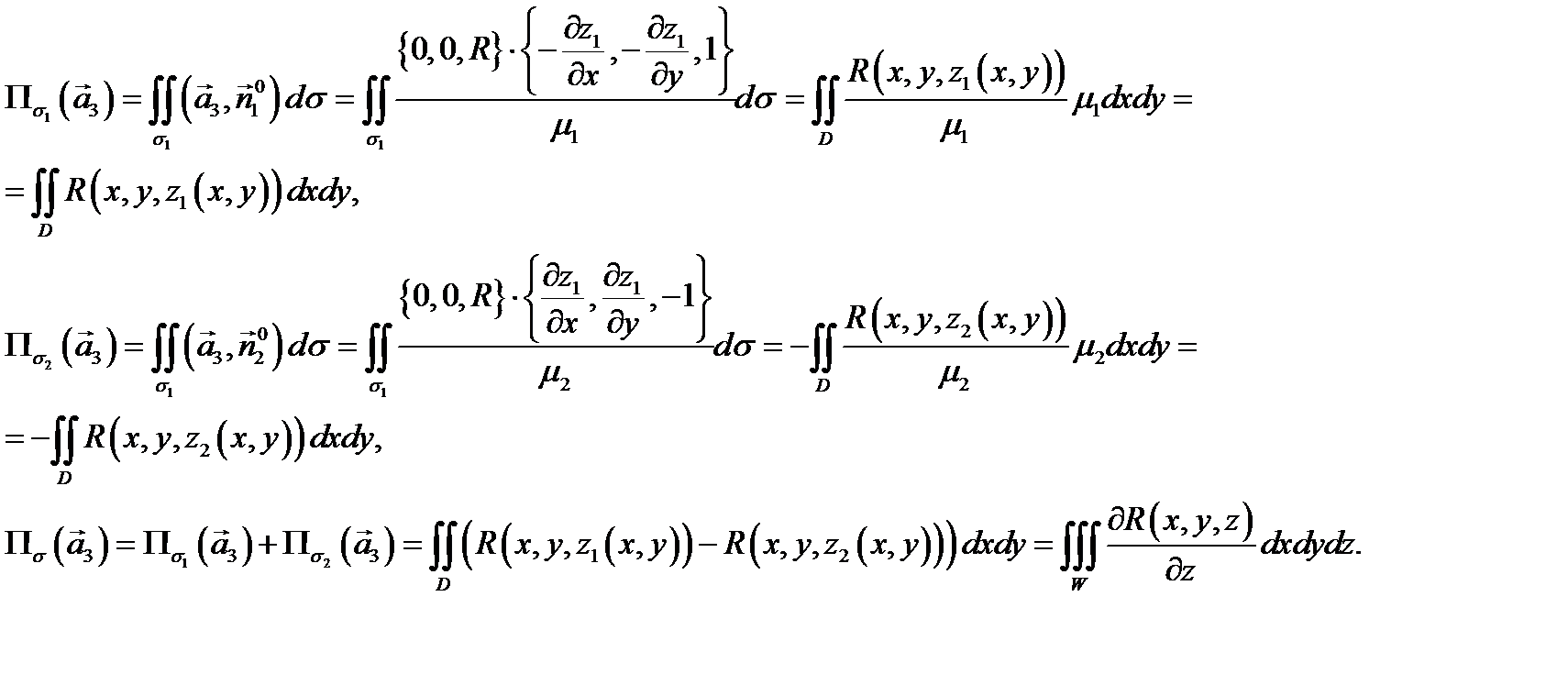
Точно так же находим, что 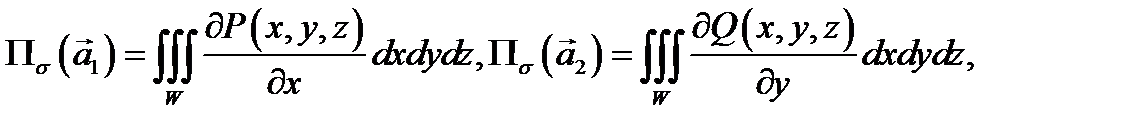
поэтому
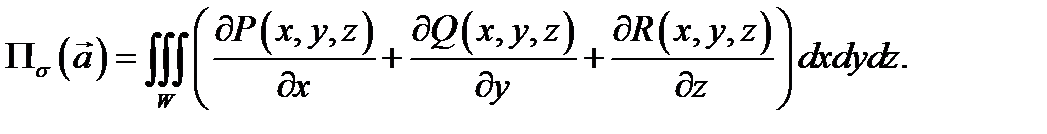
Теорема доказана.
Пример 2 (Кузнецов Л.А. Типовые расчеты).Найти поток векторного поля 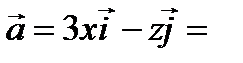
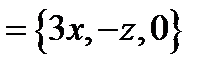 через замкнутую поверхность
через замкнутую поверхность 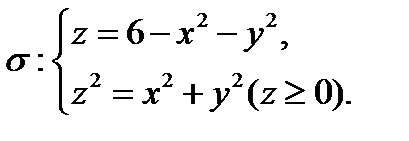 (нормаль внешняя).
(нормаль внешняя).
Решение.Воспользуемся формулой Остроградского-Гаусса:
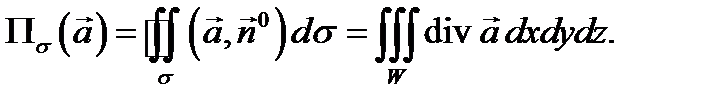
Так как 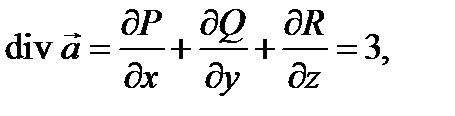 то
то 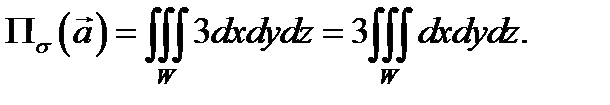
Тело
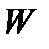 ограничено сверху поверхностью эллиптического параболоида, а снизу – поверхностью конуса. Пересечение этих поверхностей находится из системы уравнений
ограничено сверху поверхностью эллиптического параболоида, а снизу – поверхностью конуса. Пересечение этих поверхностей находится из системы уравнений
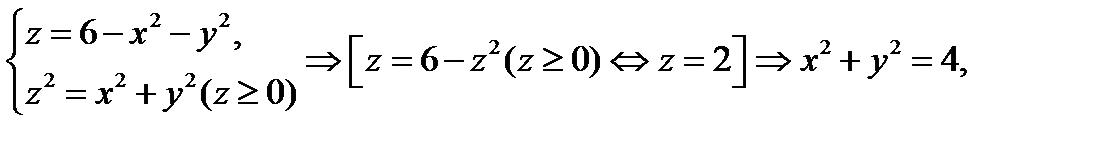
т.е. пересечение является окружностью радиуса 2. Перейдем к цилиндрической системе координат: 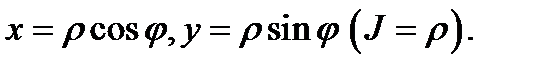 Будем иметь
Будем иметь
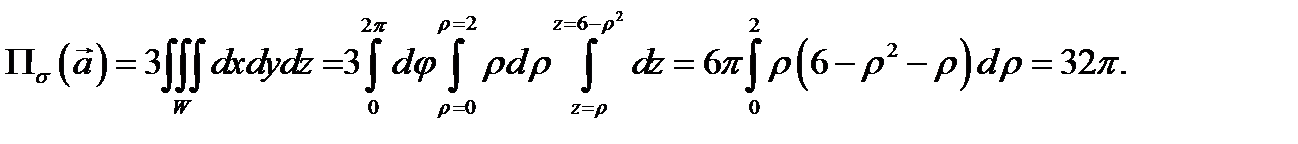
Лекции 7-8. Инвариантное определение дивергенции и её физический смысл. Соленоидальное поле. Ориентируемые кривые. Криволинейные интегралы первого и второго рода, их свойства и вычисление. Циркуляция векторного поля. Ротор. Формулы Грина и Стокса. Потенциальное поле и его свойства
Данное нами на предыдущей лекции определение дивергенции зависело от системы координат. Перейдем к описанию инвариантного определения дивергенции.
1. Инвариантное определение дивергенции и её физический смысл
Пусть векторное поле 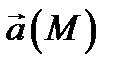 задано в области
задано в области 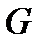 и пусть
и пусть 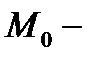 фиксированная точка этой области.
фиксированная точка этой области.
Окружим точку 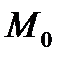 произвольной замкнутой поверхностью
произвольной замкнутой поверхностью 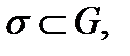 а
а 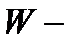 тело с границей
тело с границей 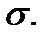 Пусть
Пусть 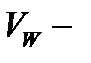 объём тела
объём тела 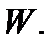
Определение 1. Если существует конечный предел 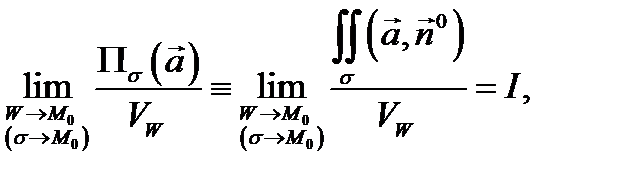
когда поверхность  стягивается в точку
стягивается в точку 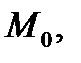 и этот предел не зависит от выбора поверхности
и этот предел не зависит от выбора поверхности 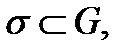 то его называют дивергенцией поля
то его называют дивергенцией поля 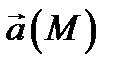 в точке
в точке 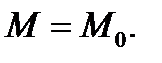
Нетрудно показать, что это инвариантное определение дивергенции совпадает с ранее данным её определением, если поле 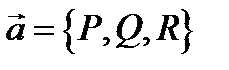 дано в декартовой системе координат. Действительно, по теореме Остроградского-Гаусса имеем
дано в декартовой системе координат. Действительно, по теореме Остроградского-Гаусса имеем
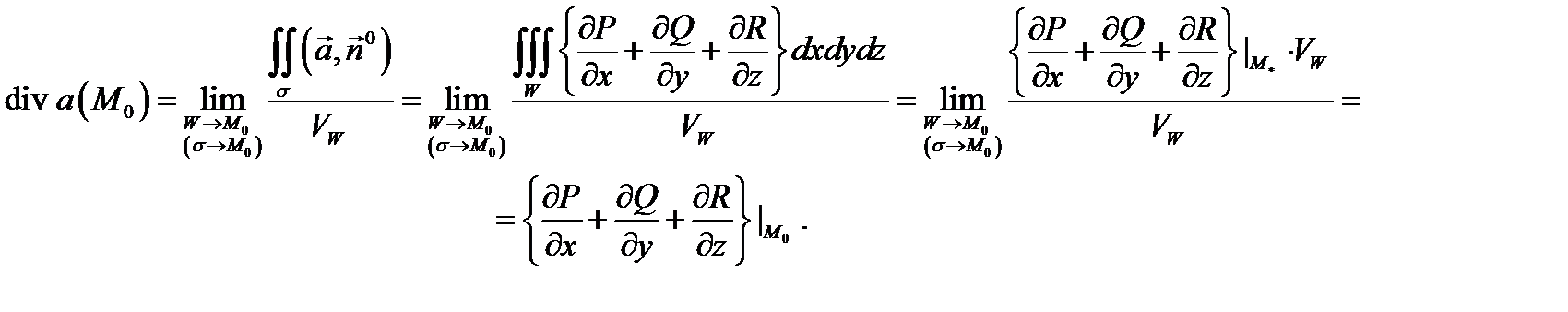
Здесь мы воспользовались теоремой о среднем и тем фактом, что при 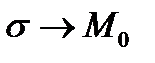 точка
точка 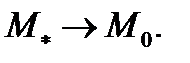 Таким образом, инвариантное определение дивергенции совпадает с ранее данным её определением в декартовой системе координат.
Таким образом, инвариантное определение дивергенции совпадает с ранее данным её определением в декартовой системе координат.
Инвариантное определение дивергенции позволяет выяснить ее физический смысл. Пусть 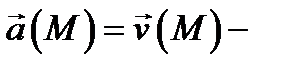 поле скоростей движующейся жидкости. Будем считать, что в области
поле скоростей движующейся жидкости. Будем считать, что в области 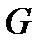 нет стоков. Тогда величина
нет стоков. Тогда величина 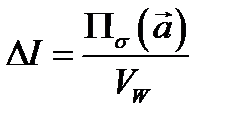 есть количество жидкости, отнесённое к объёму
есть количество жидкости, отнесённое к объёму 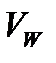 (средняя плотность мощности источников в
(средняя плотность мощности источников в 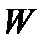 ), а предел этой величины при
), а предел этой величины при 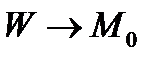 (т.е.
(т.е. 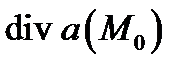 ) есть плотность мощности источников, находящихся в точке
) есть плотность мощности источников, находящихся в точке 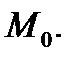
Дата добавления: 2017-03-29; просмотров: 3894;
