Сведение криволинейного интеграла второго рода по замкнутому контуру к двойному интегралу. Формула Грина
Имеет место следующее утверждение.
Теорема Грина.Пусть 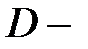 односвязная ограниченная область в
односвязная ограниченная область в 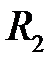 с кусочно гладкой границей
с кусочно гладкой границей 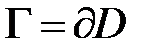 (в этом случае
(в этом случае 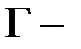 замкнутый контур) и пусть функции
замкнутый контур) и пусть функции 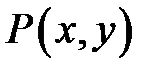 и
и 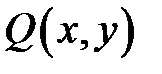 и их частные производные
и их частные производные 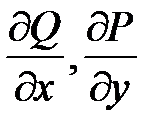 непрерывны в
непрерывны в 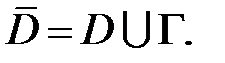 Тогда имеет место равенство
Тогда имеет место равенство
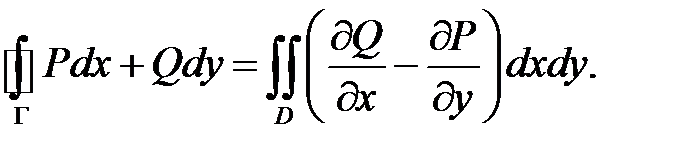

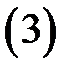
Здесь контур 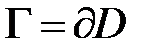 обходится так, чтобы область
обходится так, чтобы область 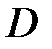 оставалась слева от наблюдателя, идущему по этому контуру.
оставалась слева от наблюдателя, идущему по этому контуру.
Доказательствопроведем для области
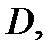 правильной в направлениях осей
правильной в направлениях осей  и
и  с гладкой границей
с гладкой границей 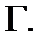 В этом случае область
В этом случае область 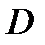 может быть описана двумя способами:
может быть описана двумя способами:
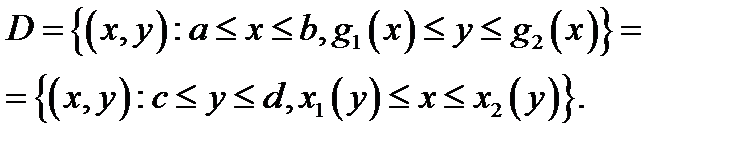
Поле  можно записать в виде
можно записать в виде 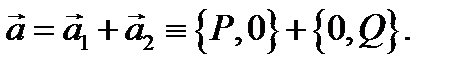 В силу линейности интеграла получаем, что
В силу линейности интеграла получаем, что
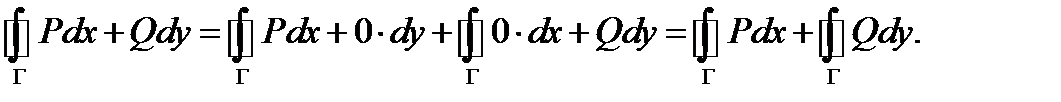

Преобразуем каждый из стоящих здесь интегралов:
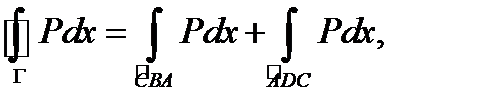
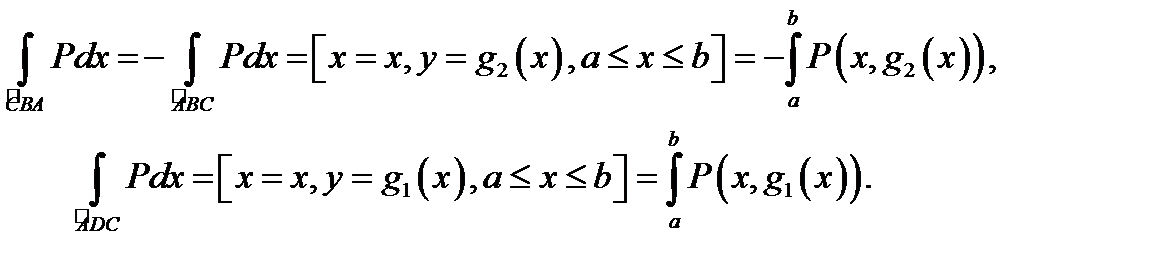
Следовательно,
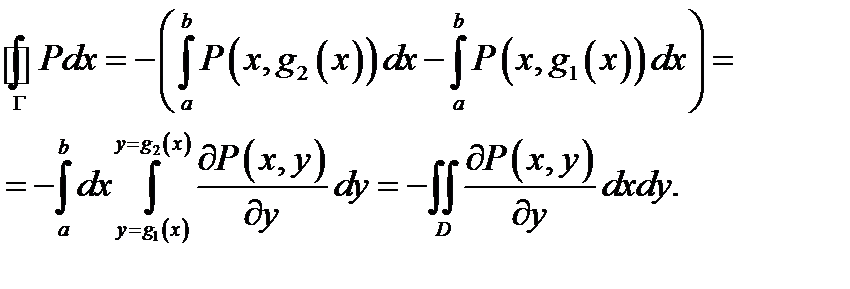
Аналогично показываем, что 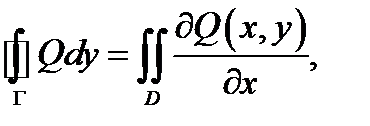 поэтому (согласно (4)) верно равенство (3).
поэтому (согласно (4)) верно равенство (3).
Теорема доказана.
Пример 1 (Кузнецов Л.А. Типовые расчеты).Найти работу силы 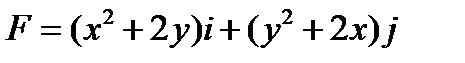 при перемещении вдоль отрезка
при перемещении вдоль отрезка 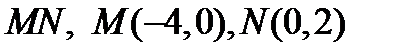 от точки
от точки 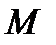 к точке
к точке 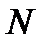 .
.
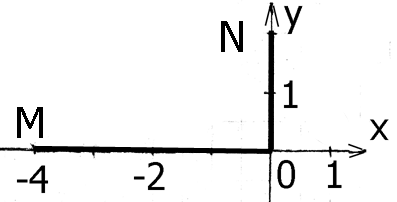 Решение.Вычисления разобьём на две части: сначала вычис-лим работу от точки
Решение.Вычисления разобьём на две части: сначала вычис-лим работу от точки 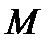 до точки
до точки  , затем – от точки
, затем – от точки  до точки
до точки 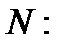
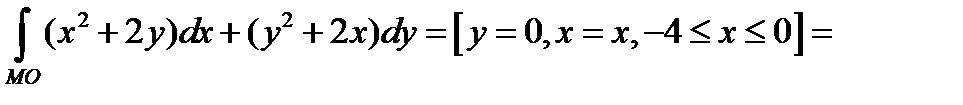
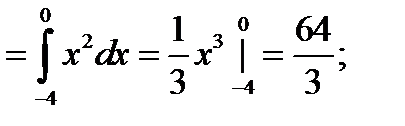

Значит, 
 Пример 2.Вычислить криволинейный интеграл
Пример 2.Вычислить криволинейный интеграл 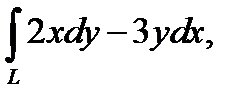 если
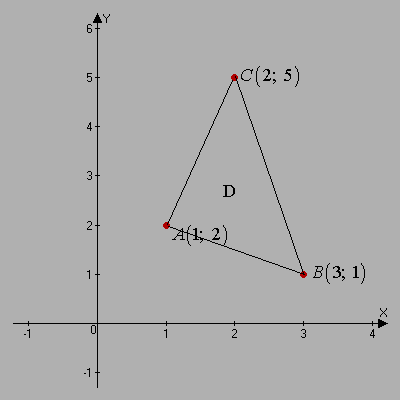
если 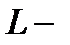 контур треугольника с вершинами
контур треугольника с вершинами 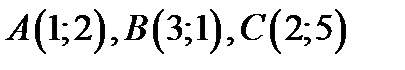 пробегаемый против часовой стрелки.
пробегаемый против часовой стрелки.
Решение.Так как контур интегрирования замкнут, то можно воспользоваться формулой Грина:
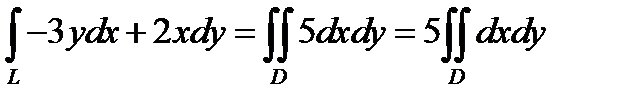 .
.
Интеграл 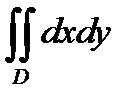 численно равен площади
численно равен площади 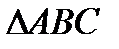 . Так как
. Так как  , то
, то 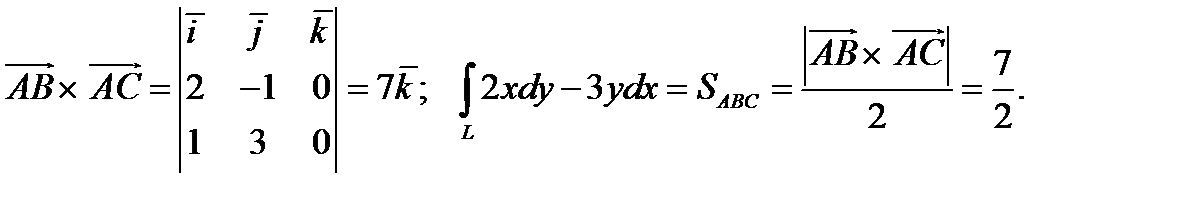
Дата добавления: 2017-03-29; просмотров: 1950;
