Ориентируемые кривые. Криволинейные интегралы первого и второго рода, их свойства и вычисление
Если на кривой 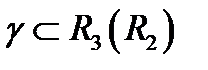 указан порядок следования её точек, то кривая
указан порядок следования её точек, то кривая 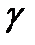 называется ориентированной кривой. Укажем на наиболее распространённые типы ориентации.
называется ориентированной кривой. Укажем на наиболее распространённые типы ориентации.
а) Кривая
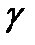 – спрямляемая дуга без точек самопересечений. Ориентация: указание начальной точки
– спрямляемая дуга без точек самопересечений. Ориентация: указание начальной точки 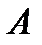 и конечной точки
и конечной точки 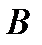 (точки следуют от
(точки следуют от 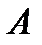 к
к 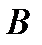 – положительная ориентация, противоположное направление – отрицательная ориентация).
– положительная ориентация, противоположное направление – отрицательная ориентация).
б) Если кривая 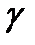 задана параметрически уравнениями
задана параметрически уравнениями 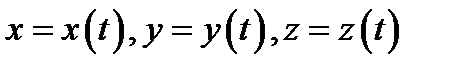
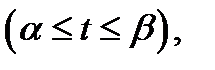 то положительная ориентация задается по возрастанию параметра
то положительная ориентация задается по возрастанию параметра 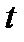 , а отрицательная ориентация – по убыванию параметра
, а отрицательная ориентация – по убыванию параметра 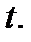
в) Если кривая 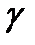 задана параметрически уравнениями
задана параметрически уравнениями 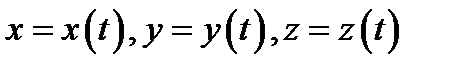
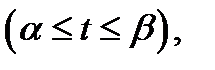 причем функции
причем функции 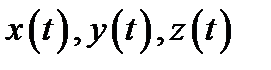 непрерывно дифференцируемы на отрезке
непрерывно дифференцируемы на отрезке 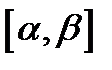 и
и 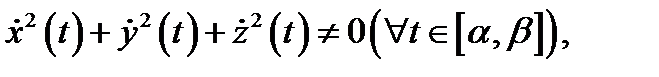 то каждая точка
то каждая точка 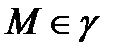 ориентируется по направлению вектора
ориентируется по направлению вектора 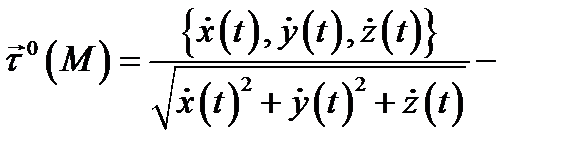 положительная ориентация; если точки кривой
положительная ориентация; если точки кривой 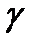 направлены по направлению вектора
направлены по направлению вектора 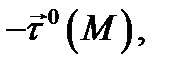 то кривая будет иметь отрицательную ориентацию.
то кривая будет иметь отрицательную ориентацию.
Кривые с положительной ориентацией обозначаются обычно 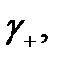 а с отрицательной ориентацией –
а с отрицательной ориентацией – 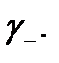 Перейдем теперь к понятию криволинейного интеграла. Сначала дадим определение криволинейного интеграла первого рода (по длине дуги).
Перейдем теперь к понятию криволинейного интеграла. Сначала дадим определение криволинейного интеграла первого рода (по длине дуги).
Пусть в пространстве задана некоторая непрерывная спрямляемая (простая) дуга 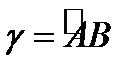 и пусть функция
и пусть функция 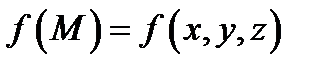 определена на этой дугу.
определена на этой дугу. Произведем разбиение
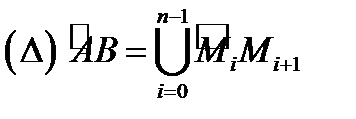 дуги
дуги 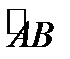 на частичные дуги
на частичные дуги 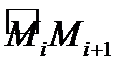 . Обозначим через
. Обозначим через 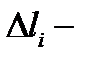 длину дуги
длину дуги 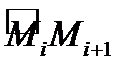 , а через
, а через 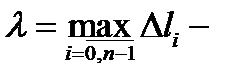 диаметр разбиения
диаметр разбиения 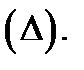 Пусть
Пусть 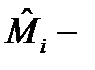 произвольная точка дуги
произвольная точка дуги 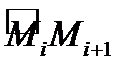 .
.
Определение 1. Если существует конечный предел интегральных сумм:
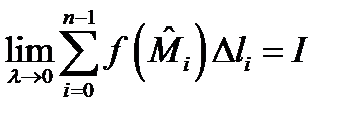 и этот предел не зависит от вида разбиения
и этот предел не зависит от вида разбиения 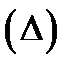 и выбора точек
и выбора точек 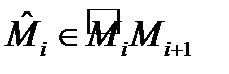 , то его называют криволинейным интегралом первого рода (по длине дуги) и обозначают
, то его называют криволинейным интегралом первого рода (по длине дуги) и обозначают 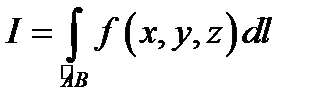 При этом функция
При этом функция 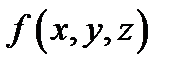 называется интегрируемой вдоль дуги
называется интегрируемой вдоль дуги 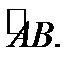
Криволинейный интеграл обладает всеми свойствами обычных интегралов. Перечислим их (везде ниже 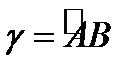 – кусочно гладкая спрямляемая дуга):
– кусочно гладкая спрямляемая дуга):
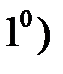 (Линейность). Если функции
(Линейность). Если функции 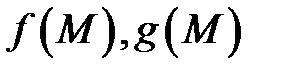 интегрируемы вдоль дуги
интегрируемы вдоль дуги 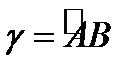 , то и функция
, то и функция 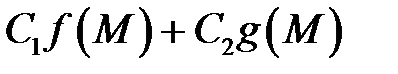 также интегрируема вдоль дуги
также интегрируема вдоль дуги 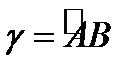 и имеет место равенство
и имеет место равенство 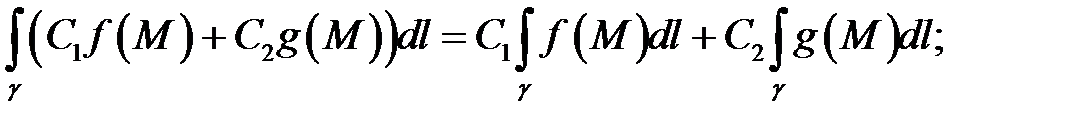
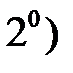 (Аддитивность). Если дуга
(Аддитивность). Если дуга 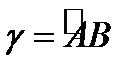 разбита точкой
разбита точкой  на две дуги
на две дуги 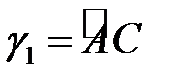 и
и 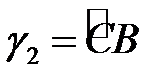 и если функция
и если функция 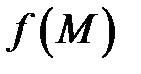 интегрируема на дуге
интегрируема на дуге 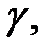 то она интегрируема и на дугах
то она интегрируема и на дугах 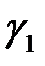 и
и 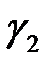 ( и обратно). При этом имеет место равенство
( и обратно). При этом имеет место равенство
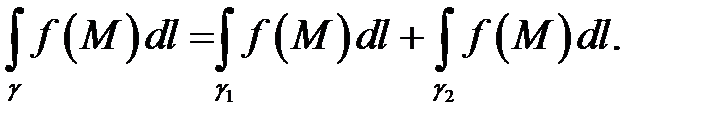
 (Теорема о среднем). Если функция
(Теорема о среднем). Если функция 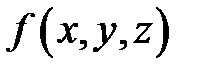 непрерывна на ограниченной кусочно гладкой спрямляемой дуге
непрерывна на ограниченной кусочно гладкой спрямляемой дуге 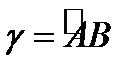 , то найдется точка
, то найдется точка 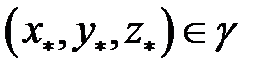 такая, что
такая, что
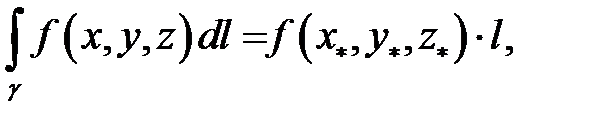 где
где 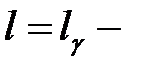 длина дуги
длина дуги 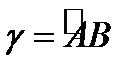 .
.
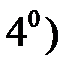 Криволинейный интеграл первого рода не зависит от ориентации дуги
Криволинейный интеграл первого рода не зависит от ориентации дуги 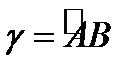 , т.е.
, т.е.
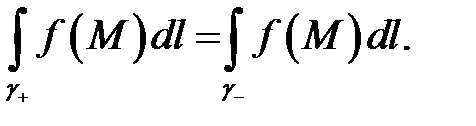
Последнее свойство следует из того, что в интегральной сумме 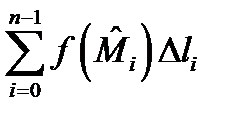 для криволинейного интеграла длина дуги
для криволинейного интеграла длина дуги 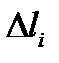 не зависит от ориентации дуги
не зависит от ориентации дуги 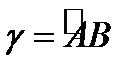 .
.
Теорема 1(о вычислении криволинейного интеграла первого рода). Пусть дуга 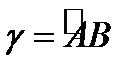 задана параметрически уравнениями
задана параметрически уравнениями 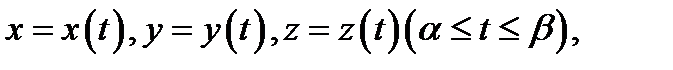 причем функции
причем функции 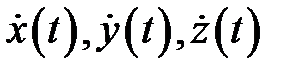 непрерывны на отрезке
непрерывны на отрезке 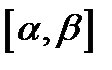 . Пусть, кроме того, функция
. Пусть, кроме того, функция 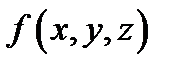 непрерывна на дуге
непрерывна на дуге 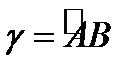 . Тогда
. Тогда
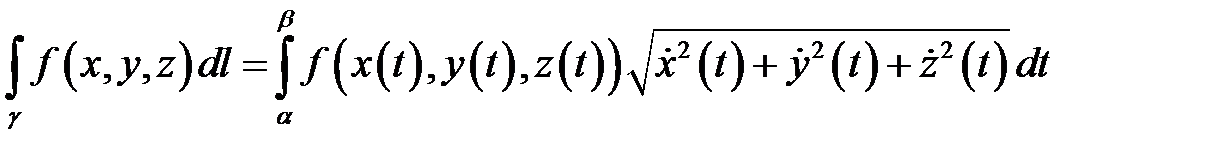 .
. 
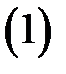
Доказательство.Воспользуемся определением криволинейного интеграла:
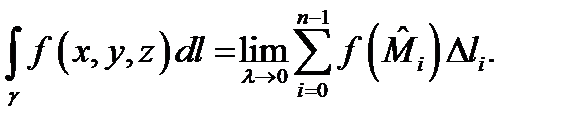
Пусть 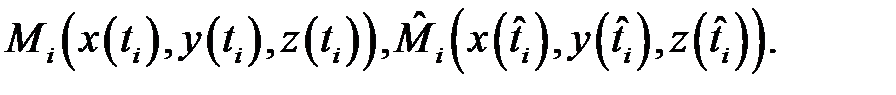 Из первого семестра нам известно, что
Из первого семестра нам известно, что 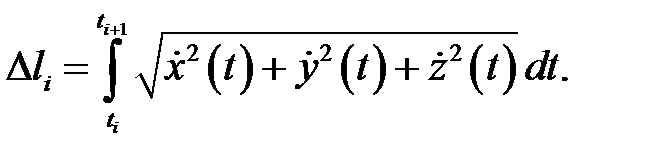 По теореме о среднем для обычного интеграла найдётся точка
По теореме о среднем для обычного интеграла найдётся точка 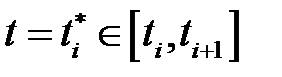 такая, что
такая, что
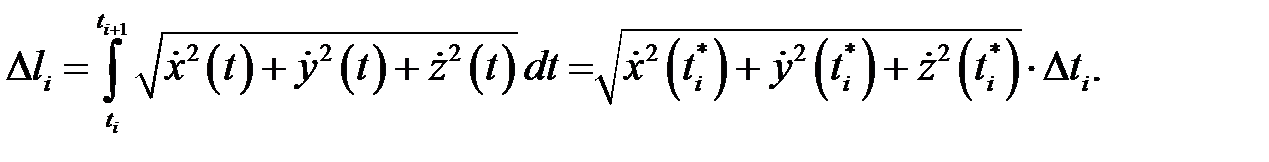
Подставляя это в интегральную сумму и учитывая, что в силу непрерывности функции 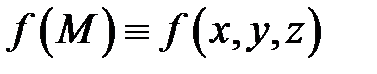 будет
будет 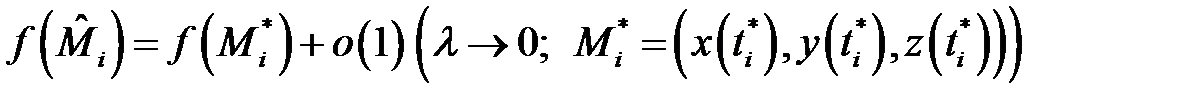 ,
,
получим
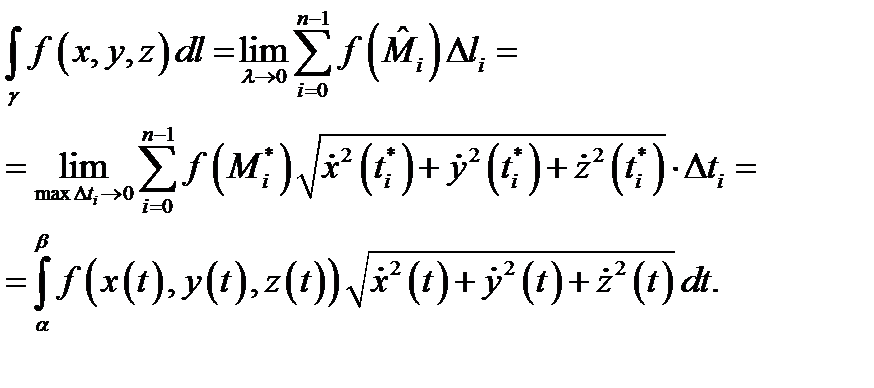
Теорема доказана.
Физический смысл криволинейного интеграла первого рода. Если 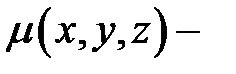 плотность стержня
плотность стержня 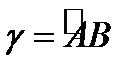 в точке
в точке 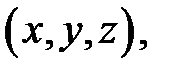 то
то 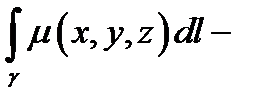 масса этого стержня (рассуждения те же самые, что и при выяснении физического смысла двойного интеграла).
масса этого стержня (рассуждения те же самые, что и при выяснении физического смысла двойного интеграла).
Перейдём теперь к понятию криволинейного интеграла второго рода (по координатам).Пусть 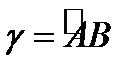 – ориентированная дуга (можно считать, что она ориентирована от начала
– ориентированная дуга (можно считать, что она ориентирована от начала 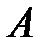 до конца
до конца 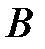 ) и пусть векторное поле
) и пусть векторное поле 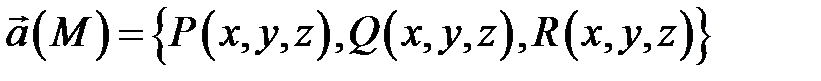 определено на этой дуге. Произведем разбиение
определено на этой дуге. Произведем разбиение 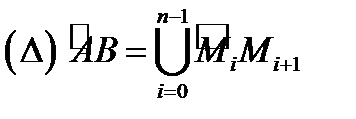 дуги
дуги 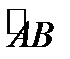 на частичные дуги
на частичные дуги 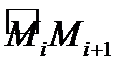 точками
точками 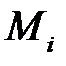 в направлении ориентации дуги
в направлении ориентации дуги 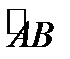 (т.е. точка
(т.е. точка 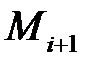 следует за точкой
следует за точкой 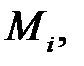 если
если 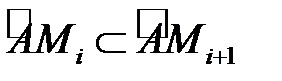 ). Обозначим
). Обозначим 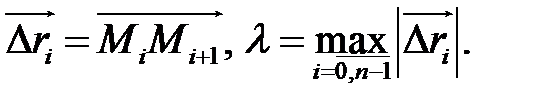 Возьмем произвольно точку
Возьмем произвольно точку 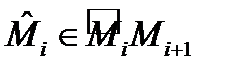 и составим интегральную сумму
и составим интегральную сумму 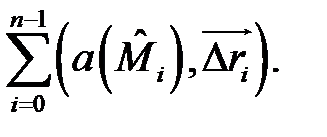
Определение 2. Если существует конечный предел интегральных сумм:
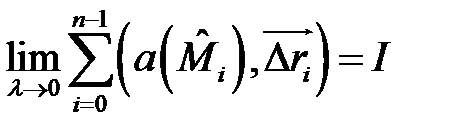
и он не зависит от вида разбиения 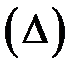 и выбора точек
и выбора точек 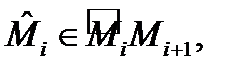 то его называют криволинейным интегралом второго рода от векторного поля
то его называют криволинейным интегралом второго рода от векторного поля
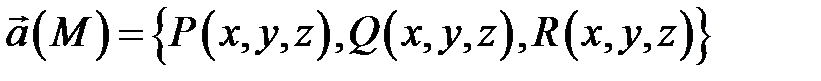
вдоль ориентированной дуги 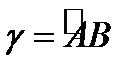 и обозначают
и обозначают 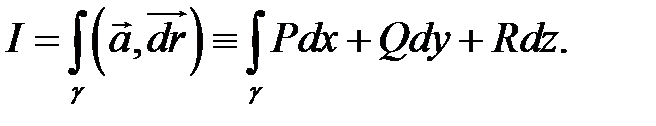 При этом поле
При этом поле 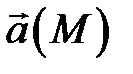 называется интегрируемым на дуге
называется интегрируемым на дуге 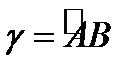 .
.
Заметим, что в криволинейном интеграле второго рода в качестве подынтегральной функции выступает скалярное произведение
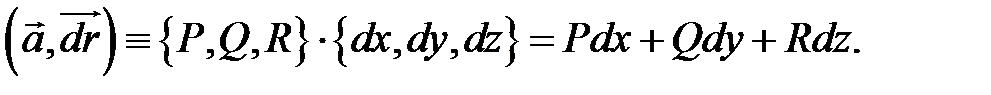
Ясно, что такой интеграл обладает всемы свойствами криволинейного интеграла первого рода, за исключением свойства 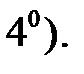 Интеграл второго рода зависит от ориентации кривой
Интеграл второго рода зависит от ориентации кривой 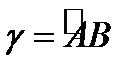 :
:
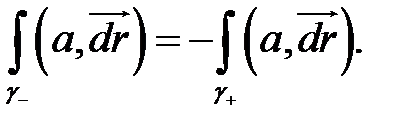
Это вытекает из того, что при изменении ориентации кривой в интегральной сумме 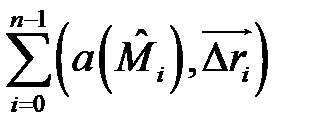 вектор
вектор 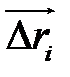 заменяется на противоположный вектор
заменяется на противоположный вектор 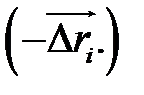
Приведем без доказательства следующее утверждение.
Теорема 2(о вычислении криволинейного интеграла второго рода). Пусть дуга 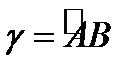 задана параметрически уравнениями
задана параметрически уравнениями 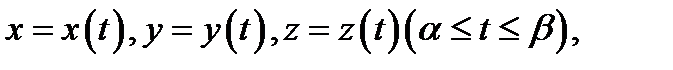 причем функции
причем функции 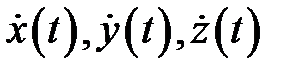 непрерывны на отрезке
непрерывны на отрезке 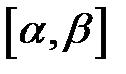 и
и 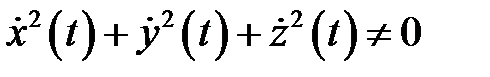
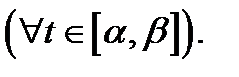 Пусть, кроме того, векторное поле
Пусть, кроме того, векторное поле
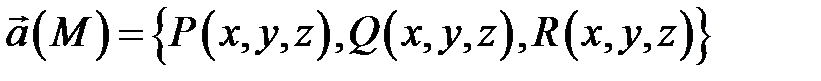
непрерывно на дуге 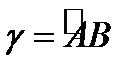 и эта дуга ориентирована по возрастанию параметра
и эта дуга ориентирована по возрастанию параметра 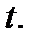 Тогда
Тогда
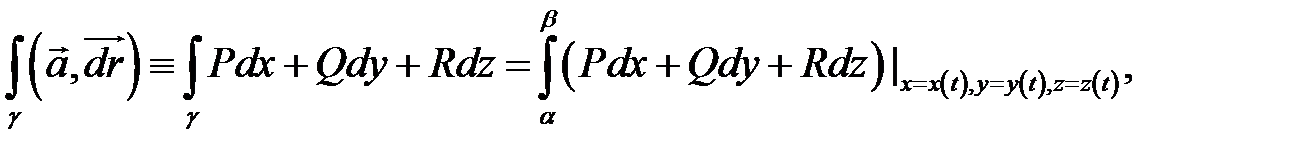
где 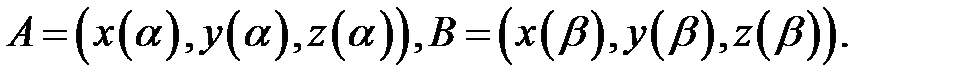
Физический смысл криволинейного интеграла второго рода состоит в следующем: если 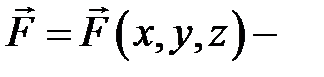 сила, действующая на материальную точку
сила, действующая на материальную точку 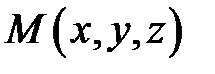 , то интеграл
, то интеграл 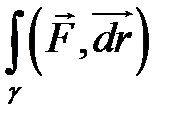 равен работе силового поля
равен работе силового поля 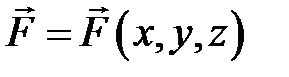 по перемещению точки
по перемещению точки 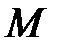 вдоль пути
вдоль пути 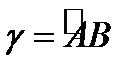 .
.
Дата добавления: 2017-03-29; просмотров: 2126;
