Потенциальное поле и его свойства

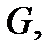Векторное поле называется потенциальным в области если оно является градиентом некоторого скалярного поля 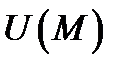(т.е. если 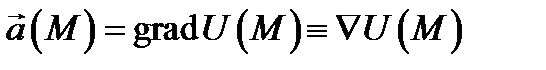в 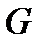). При этом скалярное поле 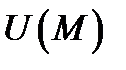называется потенциалом поля 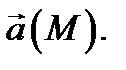Например, гравитационное поле 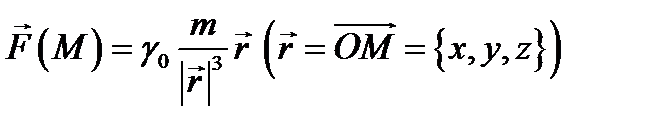является потенциальным и 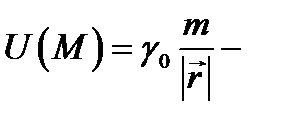его потенциал, так как 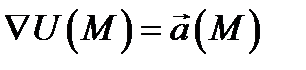(проверьте это). Потенциальное поле обладает замечательными свойствами, отличающими его от других векторных полей.

Теорема 4.Пусть векторное поле 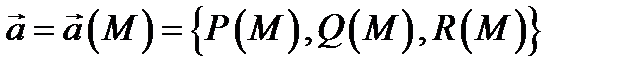непрерывно дифференцируемо в односвязной области 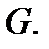Тогда справедливы следующие утверждения:

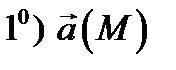потенциально в ;

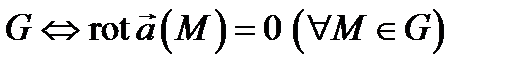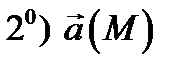потенциально в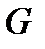 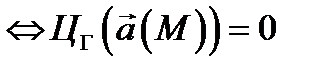(здесь 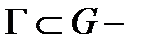произвольный кусочно гладкий контур);

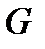
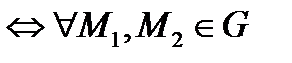потенциально в интеграл 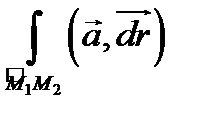не зависит от формы кусочно гладкого пути .

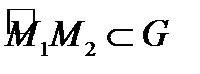В этом случае указанный криволинейный интеграл зависит только от начала 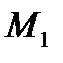и конца 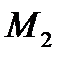и может быть вычислен по формуле

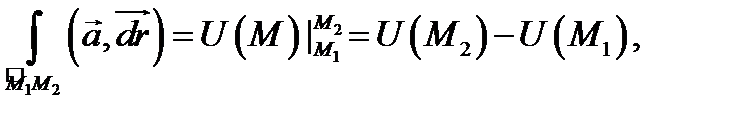где 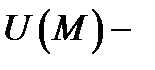потенциал векторного поля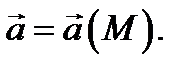

потенциально в 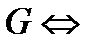выражение 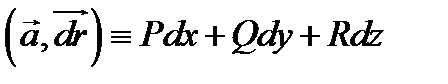является полным дифференциалом от некоторого скалярного поля 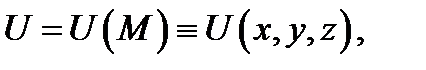т.е.

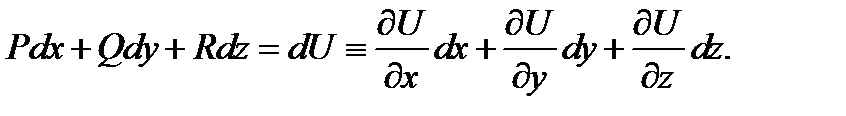
В этом случае 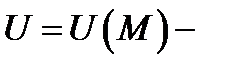потенциал поля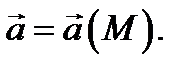

Потенциал поля 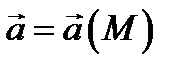(если оно потенциально) может быть вычислен по формуле

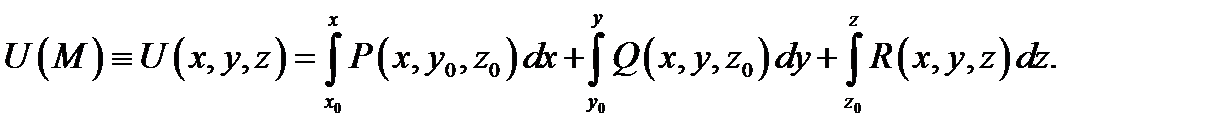
Докажем только свойства 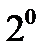и 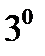(в одну сторону). Не умоляя общности, можно считать, что область является поверхностно односвязной. Применяя теорему Стокса, будем иметь 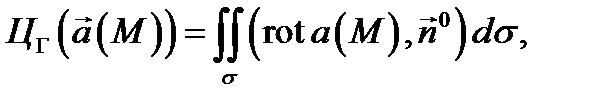где произвольная кусочно гладкая поверхность, натянутая на замкнутый контур Так как поле потенциально, то по свойству его ротор равен нулю в области 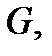а значит, 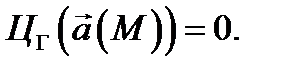Свойство 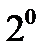доказано.

Теперь легко доказать первое утверждение свойства 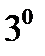. Действительно, если 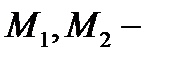две произвольные точки области 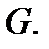Соединим их произвольными кусочно гладкими путям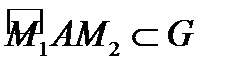и и 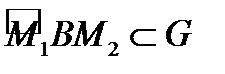. Тогда

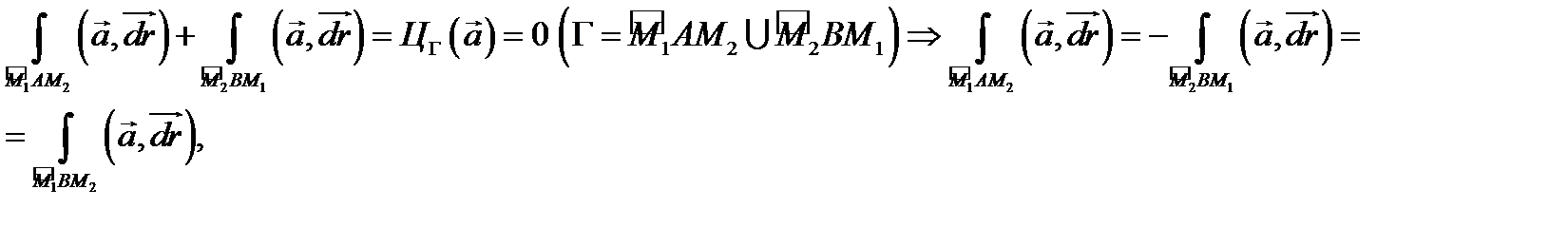т.е. интеграл 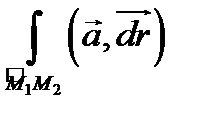не зависит от формы кусочно гладкого пути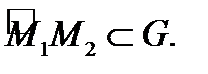

Доказательства других свойств потенциального поля не соствляет большого труда. В случае необходимости с ними можно познакомиться в любом более подробном учебнике по высшей математике.

Замечание.Если поле 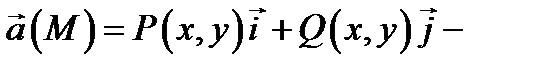плоское, то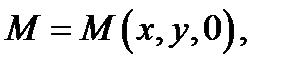 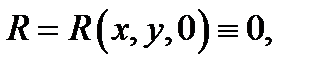поэтому ротор такого поля вычисляется по формуле

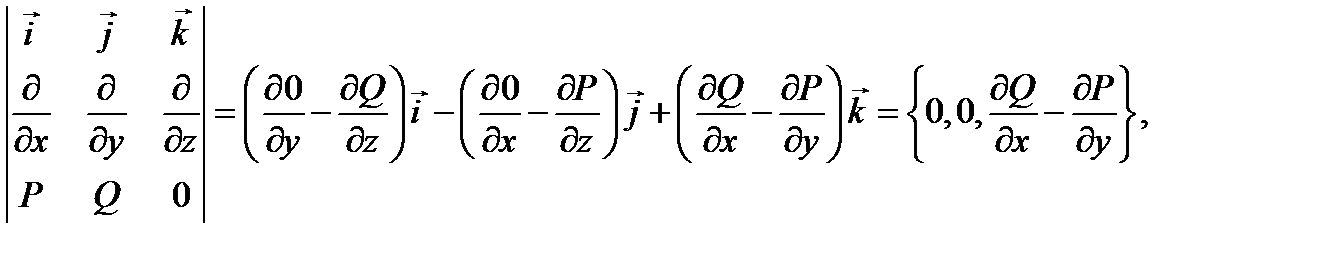
а условие потенциальности 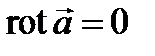приобретает вид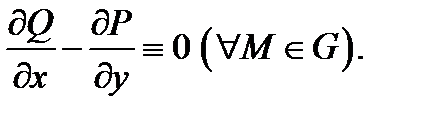

Пример 1. Вычислить криволинейный интеграл 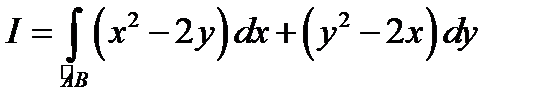от точки 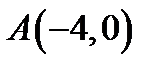до точки по двум различным путям: а) по отрезку прямой 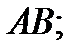б) по ломанной 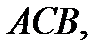где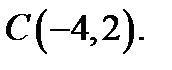

Решение.Посмотрим, будет ли это поле потенциальным. Имеем

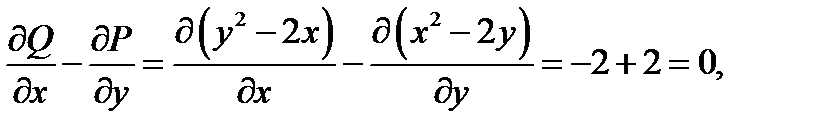
поэтому (см. замечание) это поле потенциально всюду в плоскости 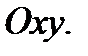Значит, криволинейный интеграл 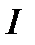не зависит от формы пути 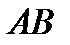. Следовательно, он будет одним и тем же, как в случае а), так и в случае б). Далее можно было бы его вычислить непосредственно (задав уравнение отрезка 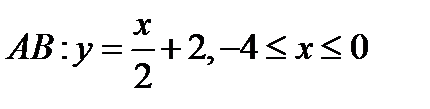), но мы вычислим его,

используя потенциал данного векторного поля. Для нахождения потенциала используем формулу (7):

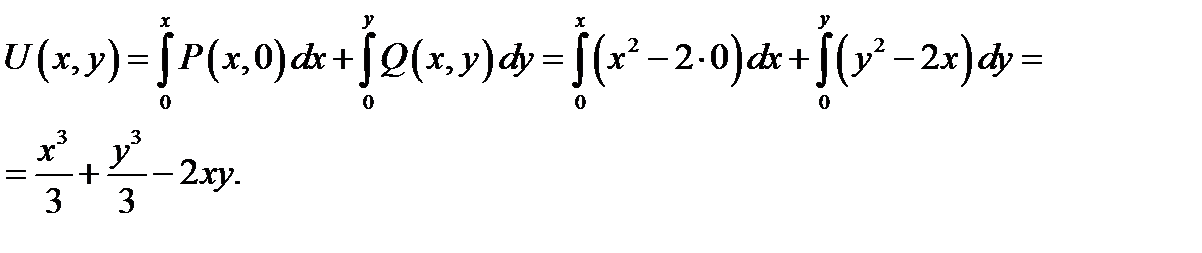
Теперь интеграл 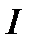вычисляется как разность потенциалов:

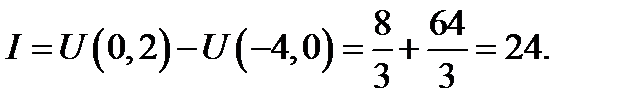
[1] Далее значок “def” и некоторые скобки в определении предела будем опускать.

[2] По определению дифференциалы независимых переменных совпадают с их приращениями.

[3] Здесь используется формула бинома Ньютона: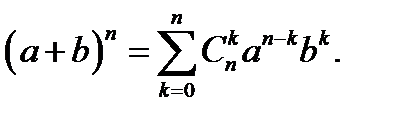

[4] Здесь 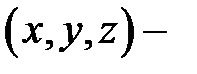произвольная (текущая) точка нормали.

[5] Заметим, что если равенство 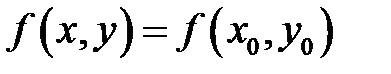достигается только в точке 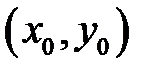, то соответствующий экстремум называется строгим экстремумом.

[6] Замкнутое ограниченное множество в 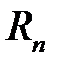называется компактом.

[7] Число связей должно быть меньше числа независимых переменных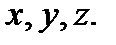

[8] Формулу (6) называют формулой Стокса.