Площадь поверхности

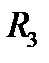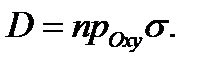Пусть в пространстве задана некоторая гладкая поверхность и пусть Произведем разбиение

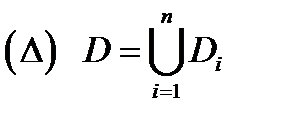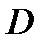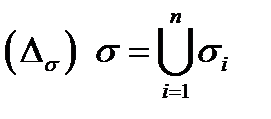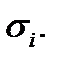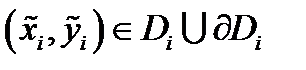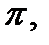области на частичные подобласти Это разбиение индуцирует разбиение поверхности на частичные поверхности Возьмем произвольно точку и в соответствующей точке построим плоскость касательную к поверхности 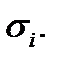Цилиндр с основанием 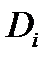и образующей, параллельной оси 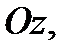вырежит из этой плоскости кусок 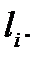Обозначим через 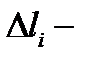площадь куска 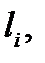а через 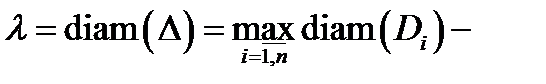диаметр разбиения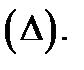

Определение 4. Если существует конечный предел 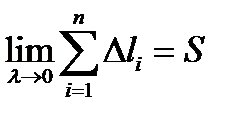и он не зависит от вида разбиения 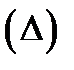и выбора точек 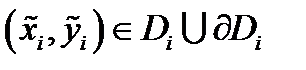, то его называют площадью поверхности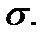

Теорема 3.Пусть поверхность задаётся уравнением 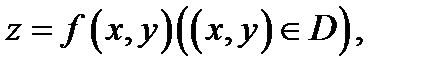причем функция 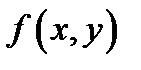и её частные производные 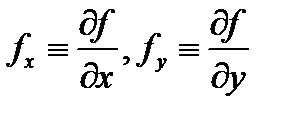непрерывны в замкнутой ограниченной области 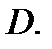Тогда площадь поверхности вычисляется по формуле

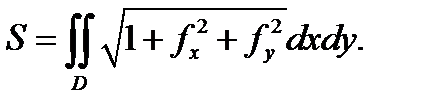
Доказательство.Вычислим площадь 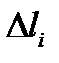куска 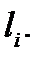Так как 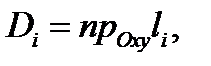то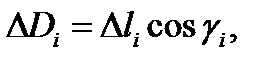

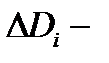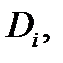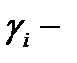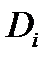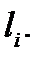где площадь области а угол между плоскостями и Угол 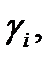очевидно, равен углу между нормалям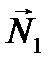и и 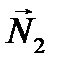плоскосте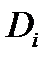й и 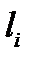соответсвенно. Так как 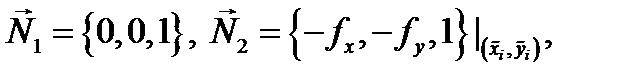то

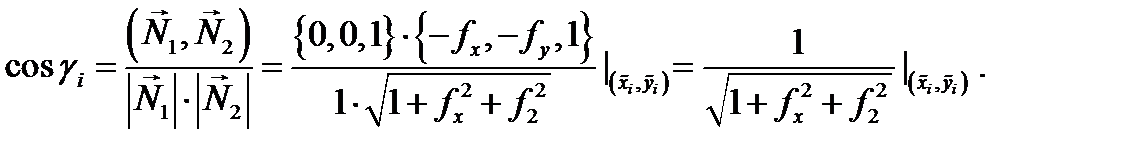
Следовательно, 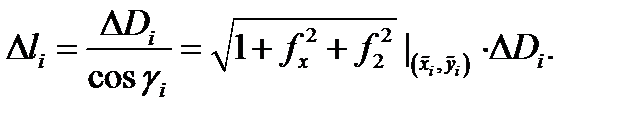По определению 4 имеем

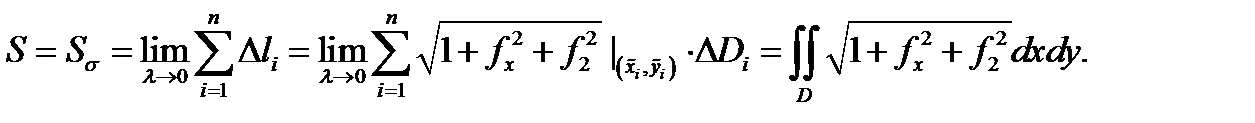
Теорема доказана.

Пример 3.Вычислить площадь части поверхности параболоида 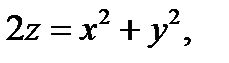вырезан-

ную цилиндром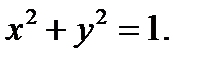

Решение.Здесь область 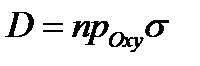есть круг 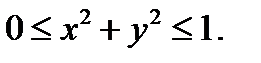Площадь искомой поверхнос-

ти находим по формуле (8):

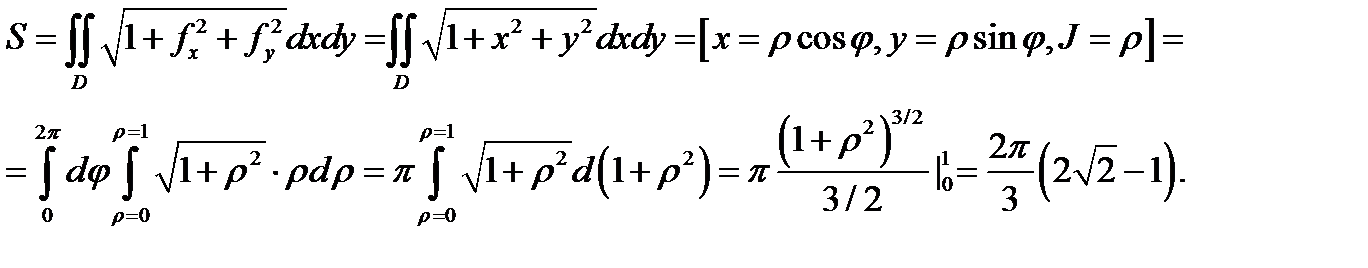
Лекция 6. Поверхностный интеграл первого рода (по площади поверхности) и его вычисление. Векторное поле. Векторные линии векторные трубки. Поток векторного поля, его свойства и вычисление. Дивергенция, её физический смысл и свойства. Формула Остроградского-Гаусса