Граничные условия на поверхности раздела
Двух проводящих сред
Граничное условие для нормальной составляющей вектора плотности электрического тока получается из принцип непрерывности электрического тока в интегральной форме 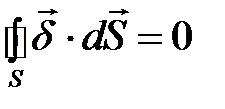 аналогично тому, как получили граничноее условиt для вектора электрического смещения (раздел 2.5). В результате имеем:
аналогично тому, как получили граничноее условиt для вектора электрического смещения (раздел 2.5). В результате имеем:
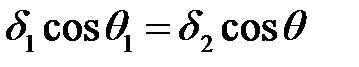 (*)
(*)
или
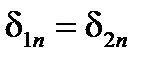
На границе раздела двух сред с различными проводимостями равны нормальные составляющие вектора плотности тока (рис.3.2а).
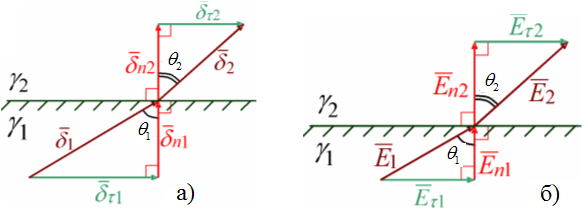
Рис.3.2. Граничное условия на грвнице разных проводящич сред сред
Граничное условие для касательной составляющей вектора напряжённости электрического поля получается из уравнения 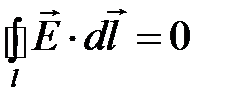 аналогично тому, как получили граничноее условие для касательной составляющей вектора напряжённости электрического поля на границе двух разных диэлектриков (раздел 2.5). В результате имеем
аналогично тому, как получили граничноее условие для касательной составляющей вектора напряжённости электрического поля на границе двух разных диэлектриков (раздел 2.5). В результате имеем
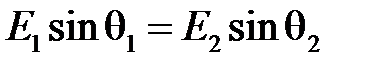 (**)
(**)
или
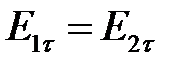 .
.
На границе раздела двух сред с различными проводимостями равны нормальные составляющие вектора плотности тока.
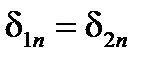
На границе раздела двух сред с различными проводимостями 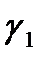 и
и 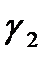 равны тангенциальные составляющие вектора напряженности поля
равны тангенциальные составляющие вектора напряженности поля 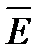 .(рис. 3.2б).
.(рис. 3.2б).
Учитывая, что плотность тока проводимости 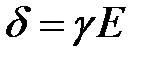 , разделив выражение (**) на (*), получим закон преломления линий тока на границе проводящих сред
, разделив выражение (**) на (*), получим закон преломления линий тока на границе проводящих сред
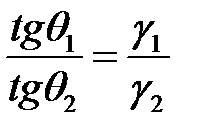 .
.
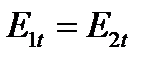 .
.
Дата добавления: 2017-08-01; просмотров: 1734;
