Векторный потенциал магнитного поля

Введем векторный потенциал магнитного поля 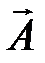, который связан с вектором магнитной индукции соотношением:

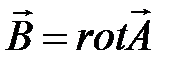. (4.2)

Получим уравнение для векторного потенциала в однородной среде.

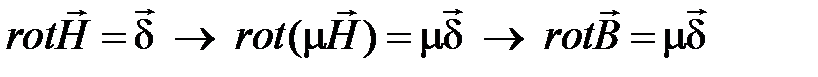. (4.3)

Подставляя (4.2) в (4.3), имеем:

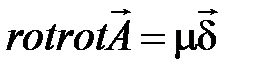. (4.4)

В соответствии с правилами векторной алгебры имеем:

,

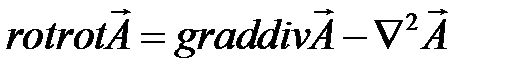тогда уравнение (4.4) примет вид:

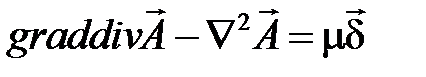(4.5)

Чтобы уравнение (4.5) стало как можно более простым пПримем .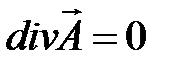

В этом случае уравнение (4.5) имеет вид

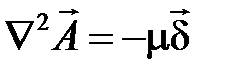. (4.6)

Одному вВекторному уравнению (4.6) соответствуют три скалярных относительно проекций вектора 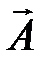в выбранной системе координат.

В декартовой системе получим:

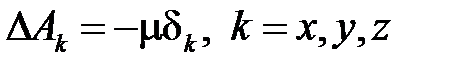(4.7)

Выражения (4.7) по форме записи совпадают с уравнением Пуассона для скалярной потенциальной функции 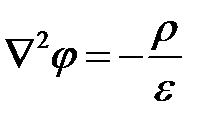. Между уравнениями существует математическая аналогия. Следовательно, решение (4.7) формально совпадает с решением уравнения Пуассона для электростатического поля.

Решение уравнения Пуассона известно и имеет вид .

Используя математическую аналогию между величинами запишем решение уравнений (4.7):

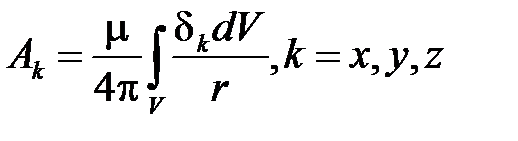, (4.8)

где 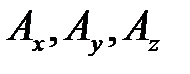— проекции вектора ;

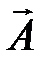― проекции вектора плотности тока;

r ― расстояние от элемента тока до точки, в которой определяется магнитное поле.

Объединя соотношения (4.8), получим решение:

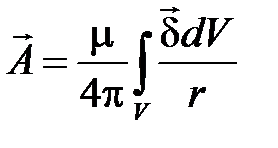. (4.9)

Решение в виде (4.8) и (4.9) получается и используется при условии существования токов в ограниченном объеме пространства, что на практике всегда имеет место. При этом, как ясно из (4.8) и (4.9), величина векторного потенциала убывает по мере удаления от области, занятой токами, в бесконечность не медленнее, чем 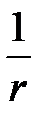. Так как магнитная индукция определяется зависимостью 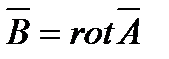, а операция 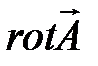есть векторно-пространственная производная, то 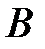и соответственно H убывают с увеличением радиуса r не медленнее, чем .

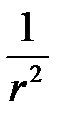Рассмотрим расчёт магнитного поля в случае линейного тока (рис.4.1).

Пусть известна плотность линейного тока δ. Тогда

,

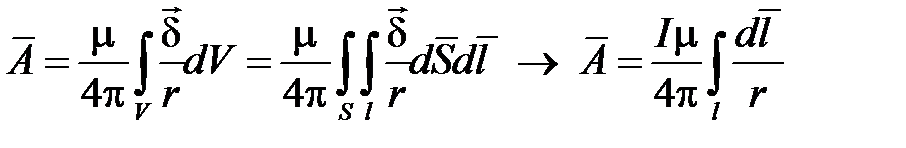так как ток .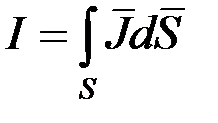

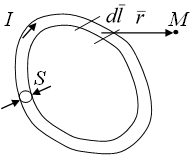
Рис.4.1.Контур с током

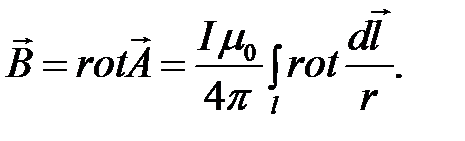(4.10)

Определим подынтегральное выражение в (4.10).

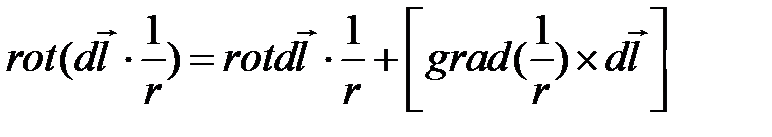
Соответственно

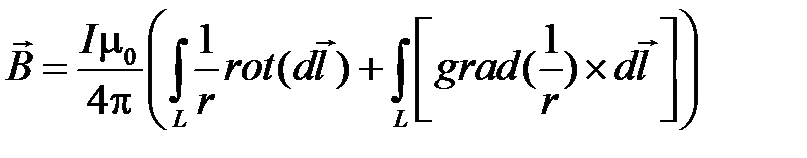
Так как dl не зависит от положения точки М, в которой находим ротор, то 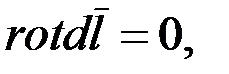а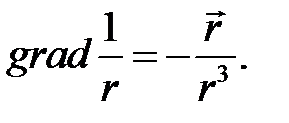

Подставив полученные результаты в уравнение (4.10) получаем

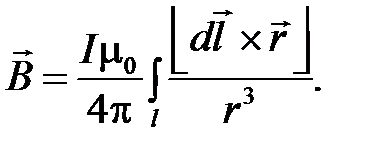
Это интегральная формулировка закона Био-Савара-Лапласа, непосредственно связывающего напряжённость магнитного поля с линейным распределением тока (рис. 4.2).

Рис. 4.2. К закону Био-Савара-Лапласа

На основе закона Био-Савара-Лапласа выполняется расчёт магнитного поля слож­ных систем проводников с токами.