Заземлитель в виде шара

Заземлитель в виде шара расположен на сравнительно не­большой глубине h, соизмеримой с его радиусом R (рис.3.5). На рис.3.5 указаны граничные условия.

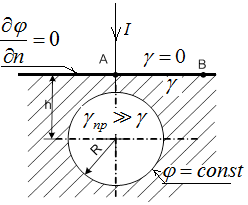
Рис.3.5

Применим к решению задачи метод электростатической аналогии.

Аналогичная электростатическая задача представлена на рис.3.6,а.

Применим к решению задачи метод зеркальных отображений. Дополним верхнюю полуплоскость диэлектриком 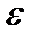и зеркально расположим там такой же шар с зарядом q, при этом граничные усло­вия на поверхности раздела сред не из­менятся (рис.3.6,б) .

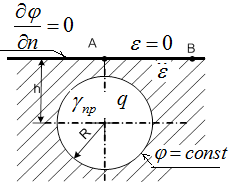а)

б)

Рис.3.6

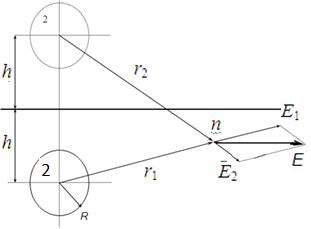
Расчёт потенциала поля в произ­вольной точке n производится по методу наложения:

.

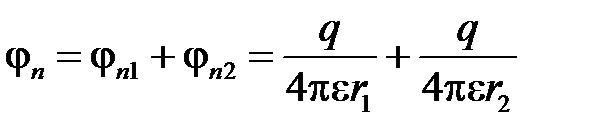При соотношении h>>R неравномерностью распределения заряда по поверхности шара пренебрегаем. Тогда потенциал на поверхности заземлителя будет ра­вен:

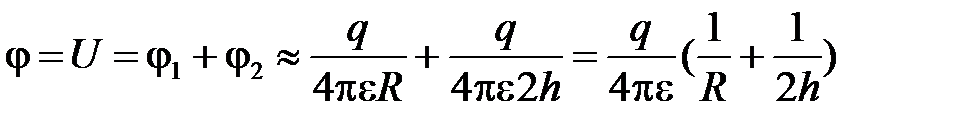, откуда следует формула для определения емкости:

.

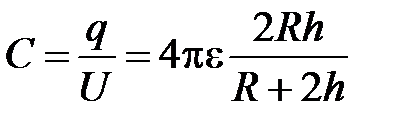Для исходной задачи поля токов будем иметь.

.

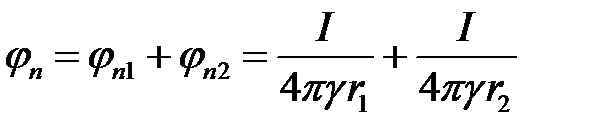Проводимость заземлителя:

.

Вопросы для самопроверки

1. Электрический ток является векторной или скалярной величиной?

2. Как определить емкость двухпроводной линии путем моделирования ее полем постоянных токов ?

3. Что такое "шаговое" напряжение, как его рассчитать?