Метод электростатической аналогии
Между величинами, характеризующими электростатическое поле и электрическое поле постоянного тока в проводящей, существует полная математическая аналогия.
Аналогия электростатического поля в области, где нет свободных зарядов, и поля стационарных токов в проводящих средах, где нет сторонних сил, обусловлена полной аналогией соответствующих уравнений и граничных условий щ(табл.1).
Таблица 1
| Электрическое поле постоянного тока | Электростатическое поле при отсутствии зарядов (r=0) |
| 
|
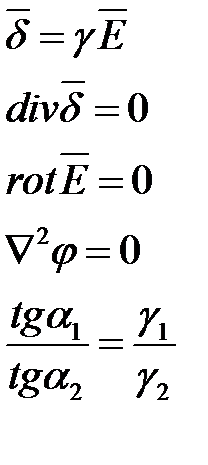
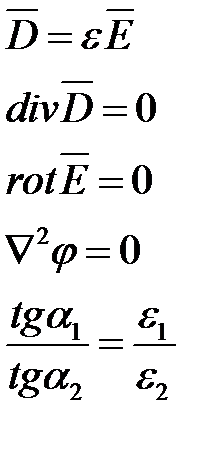
Можно сделать вывод об аналогии между зарядом q и током i , и между емкостью C и проводимостью g. Действительно, емкость между двумя телами, находящимися в среде с абсолютной диэлектрической проницаемостью ε , равна
. (1)
Проводимость между этими проводящими телами, помещенными в проводящую среду с удельной проводимостью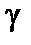 
можно записать как:
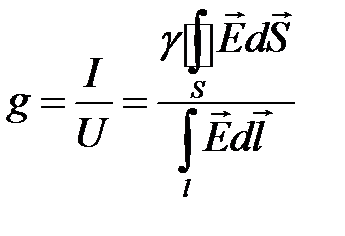. (2)
Поделив (1) на (2), получим:
.
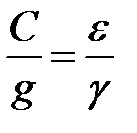Отмеченная аналогия лежит в основе расчёта полей методом электростатической аналогии. Этот метод позволяет в ряде случаев при расчёте токов в проводящей среде воспользоваться готовыми аналитическими решениями аналогичных задач электростатики.
Аналогичными задачами являются задачи с одиаковой геометрией и одинаковми граничными условиями.
3.2.4. Расчёт тока утечки коаксиального кабеля
Изоляция коаксиального кабеля выполнена двухслойной (удельные проводимости : g1 = 5·10-8 См/м и g2 = 2·10 -8 См/м; диэлектрические проницаемости er1 = 2 и er2 = 5). Напряжение U = 10 кВ. Геометрические размеры – r1 = 1 мм, r2 = 2 мм, r3 = 3 мм.
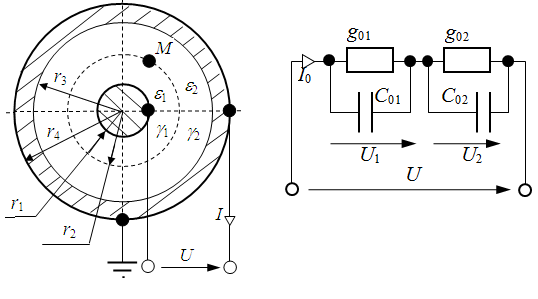
Рис.3.3.
Найти удельные тепловые потери в окрестности точки М, проводимости и ёмкости между телами, построить схему замещения системы.
Воспользуемся аналогией между электрическим полем в проводящей среде и электростатическим. ёмкости слоёв данного кабеля:
C10 =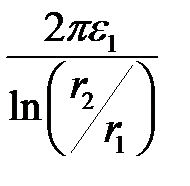 
= 
= 160,4 пФ/м;
C20 =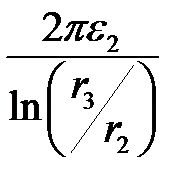 
= 
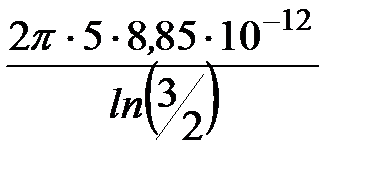= 873,5 пФ/м.
Проводимости слоёв и всего кабеля на единицу длины:
g10 = 
= 
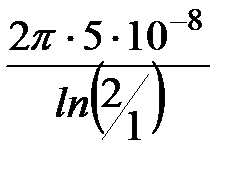= 0,454·10-6 Cм/м;
g20 =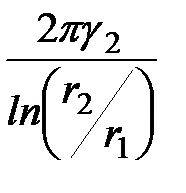 
= 
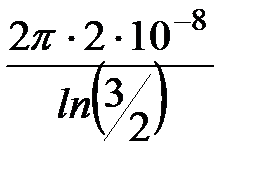= 0,310·10-6 Cм/м;
g0 =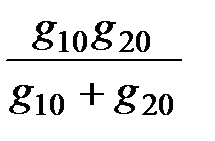 
= 
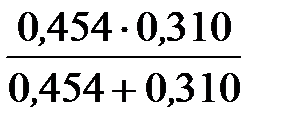= 0,1842 мкСм/м.
Плотность тока в окрестности точки М:
d = i0/(2pr2) = 1,841·10-3/(2p ·2·10-3) = 0,147 А/м2.
Удельные тепловые потери в окрестности точки М в слоях изоляции:
p1 = d 2/g1 = 0,1472/(5·10-8) = 0,432·106 Вт/м3 = 0,432 МВт/м3;
p2 = d 2/g2 = 0,1472/(2·10-8) = 1,08·106 Вт/м3 = 1,08 МВт/м3.
Дата добавления: 2017-08-01; просмотров: 2362;