Выражение магнитного потока и энергии
Через векторный потенциал
Магнитный поток, пронизывающий через поверхность S (рис. 4.3) равен:
индукцию 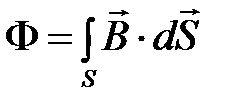 . (4.11)
. (4.11)
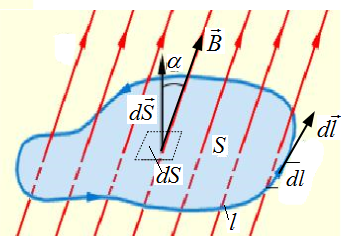
Рис. 4.3. К определению магнитного потока
На основании теоремы Стокса поверхностный интеграл может быть преобразован в линейный:
Используя теорему Стокса, получим: 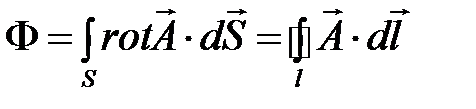 . (4.12)
. (4.12)
(4.11)
Магнитный поток 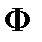 сквозь поверхность
сквозь поверхность 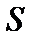 равен линейному интегралу от векторного потенциала
равен линейному интегралу от векторного потенциала 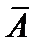 по замкнутому контуру, ограничивающему эту поверхность.
по замкнутому контуру, ограничивающему эту поверхность.
Определение потока по (4.12) часто имеет преимущества по сравнению с определением потока через магнитную индукцию (4.11). Соотношением (4.11) можно пользоваться в том случае, когда известно значение 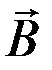 в любой точке поверхности S, тогда как для вычисления потока с помощью соотношения (4.12) достаточно знать значение на контуре и не требуется значения
в любой точке поверхности S, тогда как для вычисления потока с помощью соотношения (4.12) достаточно знать значение на контуре и не требуется значения 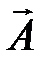 в точках внутри контура.
в точках внутри контура.
Для вычисления магнитного потока 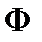 по формуле (4.11) достаточно знать векторный потенциал
по формуле (4.11) достаточно знать векторный потенциал 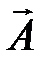 только на контуре, ограничивающем эту поверхность.
только на контуре, ограничивающем эту поверхность.
Известно, что с магнитным полем связана энергия, распределенная в пространстве с плотностью
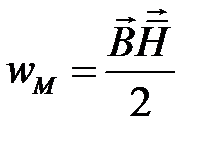 .
.
В некоторой области V энергия определяется интегралом
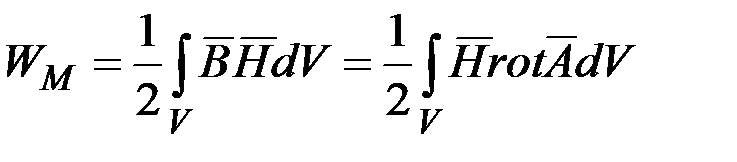 , так как
, так как 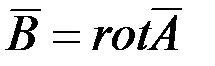 .
.
Используя равенство 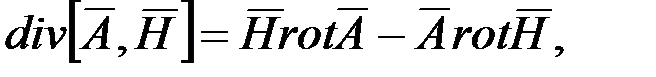 получим
получим
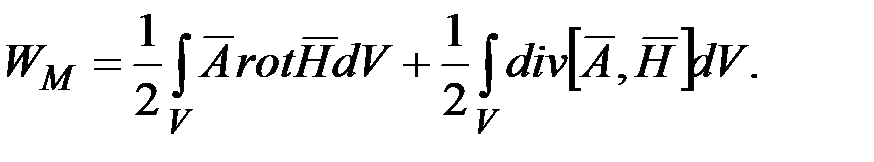
Преобразуем второе слагаемое по теореме Остроградского-Гаусса
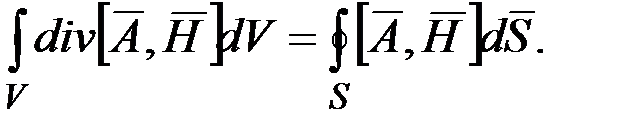
При учете всей энергии поля подынтегральное выражение в последней формуле устремляется к нулю, так как произведение векторного потенциала и напряжености магнитного поля убывает быстрее, чем r –2, а площадь увеличивается пропорционально r2. Таким образом, с учетом 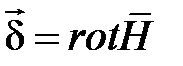 получаем:
получаем:
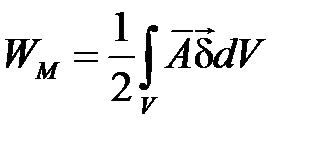 . (4.1213)
. (4.1213)
Необходимо отметить, что величина 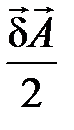 не является плотностью энергии. Если предположить, что
не является плотностью энергии. Если предположить, что 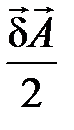 — плотность энергии магнитного поля, то немедленно следует, что вся энергия магнитного поля заключена в области, где
— плотность энергии магнитного поля, то немедленно следует, что вся энергия магнитного поля заключена в области, где 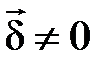 (например, в проводах). Однако физически данное утверждение неверно, так как энергией обладают все точки, где
(например, в проводах). Однако физически данное утверждение неверно, так как энергией обладают все точки, где 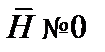 . Выражение (4.1213) просто устанавливает связь между энергией поля и векторным потенциалом
. Выражение (4.1213) просто устанавливает связь между энергией поля и векторным потенциалом 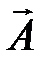 .
.
Дата добавления: 2017-08-01; просмотров: 767;
