Плоскопараллельное магнитное поле
Если мысленно рассечь электростатическое поле какой-либо секущей плоскостью, то в полученном сечении будут видны следы пересечения плоскости с эквипотенциальными поверхностями. Их называют эквипотенциальными линиями.
Магнитное поле на плоскости можно наглядно представить совокупностью силовых и эквипотенциальных линий — картиной поля.
Плоскопараллельное поле — поле картина которого повторяется во всех плоскостях, перпендикулярных какой-либо оси декартовой системы координат (рис.4.54).
Для плоскопараллельного поля уравнение линии равного потенциала:
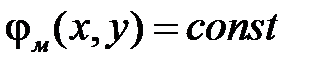 .
.
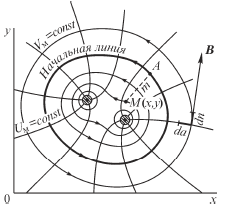
Рис.4.54. Картина поля
Плоскопараллельное поле — поле картина которого повторяется во всех плоскостях, перпендикулярных какой-либо оси декартовой системы координат (рис.4.5).
Для плоскопараллельного поля уравнение линии равного потенциала:
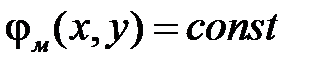 .
.
Для описания силовых линий введем понятие функции потока Vм. Одну из силовых линий примем за начальную (нулевую), полагая на ней 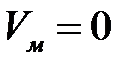 (рис4.5). Соединим произвольную точку M(x,y) c некоторой точкой А начальной линии отрезком MmA. Обозначим через
(рис4.5). Соединим произвольную точку M(x,y) c некоторой точкой А начальной линии отрезком MmA. Обозначим через 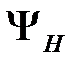 поток вектора
поток вектора 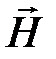 сквозь поверхность, которую описал бы отрезок MmA, перемещаясь параллельно самому себе в напралении оси 0z и проходя путь l. Поток на единицу длины обозначим как
сквозь поверхность, которую описал бы отрезок MmA, перемещаясь параллельно самому себе в напралении оси 0z и проходя путь l. Поток на единицу длины обозначим как 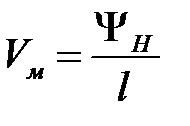 .
.
Велчина Vм, зависит от положения точки M , т.е. является функцией ее координат, что запишем в виде Vм (x, y). Функция Vм (x, y) имеет постоянное значение на выбранной силовой линии. Поэтому уравнение
Vм (x, y)=const
является уравнением этой силовой линии.
Функцию V (x, y) называют фунуцией потока.
Функция потока в данной точке равна потоку вектора 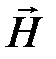 в трубке, ограниченной силовыми линиями — проходящей через данную точку и начальной силовой линией.
в трубке, ограниченной силовыми линиями — проходящей через данную точку и начальной силовой линией.
Эквипотенциальные и силовые линии в любой точке поля пересекаются под прямым углом, т. е. образующих в плоскости x0у ортогональную сетку (рис.2.74). Пусть dn — элемент длины линии напряженности поля и dτ — элемент длины линии равного потенциала. Координату n будем считать возврастающей в направлении вектора 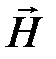 . Координату τ будем считать возврастающей влево от вектора
. Координату τ будем считать возврастающей влево от вектора 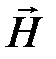 для наблюдателя, расположившегося так, что для него вектор
для наблюдателя, расположившегося так, что для него вектор 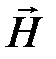 направлен снизу вверх. Примем, что функция Vм возврастает в том же направлении, в котором увеличивается координата τ. При этих условиях напряжённость электрического поля выражена через
направлен снизу вверх. Примем, что функция Vм возврастает в том же направлении, в котором увеличивается координата τ. При этих условиях напряжённость электрического поля выражена через 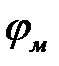 и V м в форме
и V м в форме
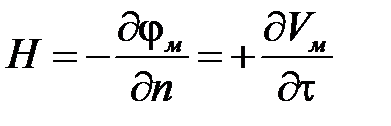 .
.
Дата добавления: 2017-08-01; просмотров: 2404;
