Магнитное поле и индуктивность двухпроводной линии

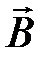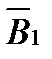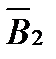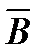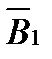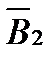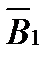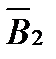Результирующий вектор магнитной индукции в произвольной точке n можно определить по методу наложения как геометрическую сумму составляющих этого вектора и от каждого провода в отдельности: = + . Составляющие вектора и определяются по полученным ранее формулам, а их направления — по правилу правоходового винта:

, .

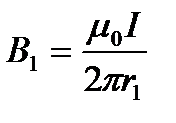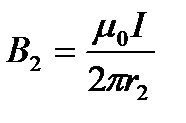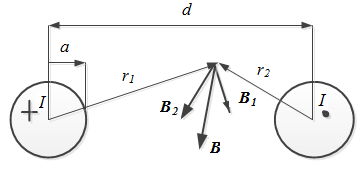
Рис.4.9. Двухпроводная линия

Индуктивность линии равна .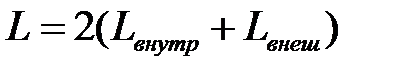

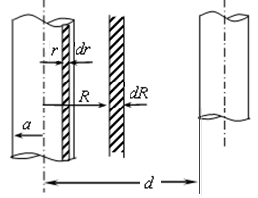
Рис.4.10. Красчету индуктивности

Внутренняя индуктивность одного проводника

.

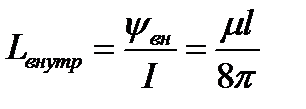Определим потокосцепление между проводниками

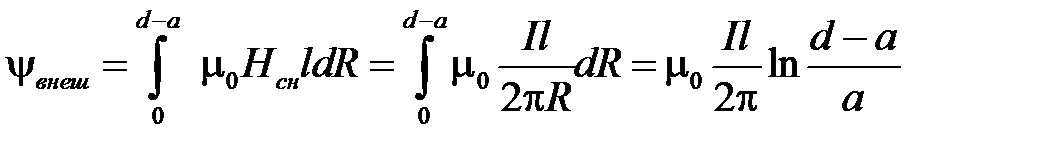
Тогда .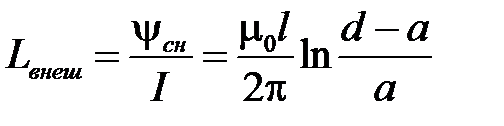

Таким образом, индуктивность двухпроводной линии равна

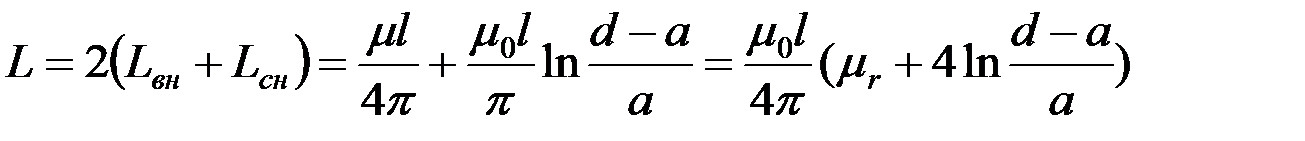[ Гн / м].

При : .

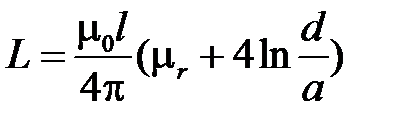Условная индуктивность на один провод

.

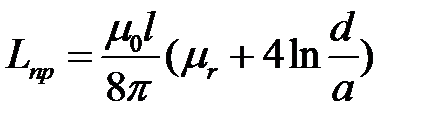Общие выражения для взаимной и собственной индуктивностей контуров из линейных проводников

Получим выражение для взаимной индуктивности двух контуров произвольно заданной формы (рис.4.11). Для этого введем допущения: контуры находятся в воздухе; материал проводников немагнитный.

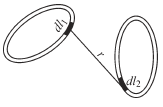
Рис.4.11. К определению взаимной индуктивности двух контуров

Найдем 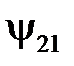потокосцепление со вторым контуром от тока, действующего в первом контуре. Для контуров из линейных проводников поперечные сечения малы по сравнению с l и r, тогда

.

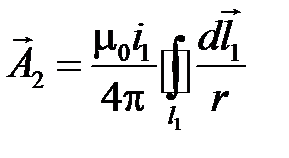Потокосцепление 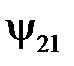при этом может быть принято равным потоку сквозь поверхность, ограниченную осью проводника второго контура, т.е.

.

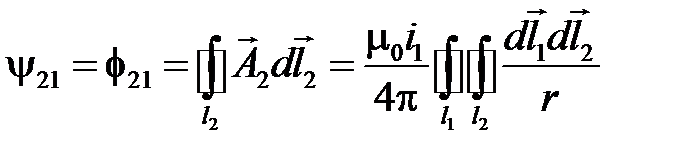Разделив 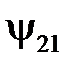на 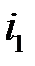, получаем

.

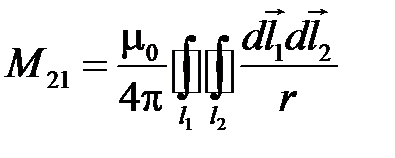Индуктивность контура из тонкого проводника.

Представим потокосцепление в виде суммы Ψ = Ψ _внеш + Ψ _внутр. Для одного витка .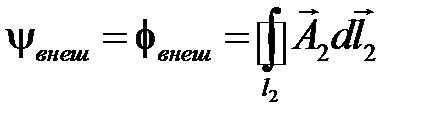

Величину 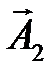приближенно вычислим по формуле: .

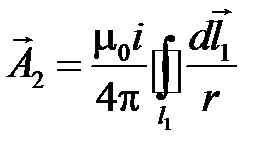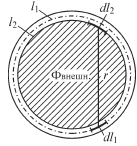
Рис.4.12. К определению собственной индуктивности котура

Таким образом, .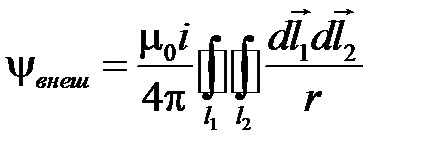

Потокосцепление внутреннее найдем как внутреннее потокосцепление на отрезке l₁ бесконечно длинного провода при условии .

Индуктивность контура найдем как сумму внешней и внутренней индуктивности L = L _внеш + L _внутр,которая для тонкого провода будет рассчитываться как

.

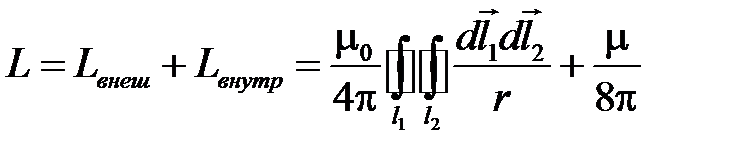4.12.Метод участков расчёта индуктивностей

Метод участков основан на условных понятиях о взаимной индуктивности между участками проводников и об индуктивностях участков проводников.

Пусть имеется два контура. Разобьем первый контур на m участков и второй контур на n участков (рис.4.13). Разбивая в выражении для M₂₁ интегралы по замкнутым контурам на суммы интегралов, взятых вдоль участков контуров, будем иметь

.

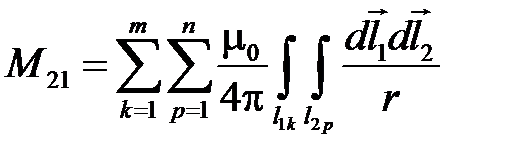Выражение, стоящее под знаком двойной суммы, можем рассматривать как взаимную индуктивность 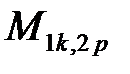между k участком первого контура и p участком второго контура. Таким образом,

.

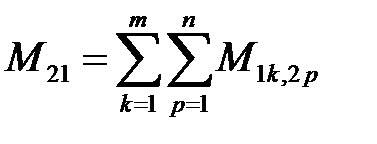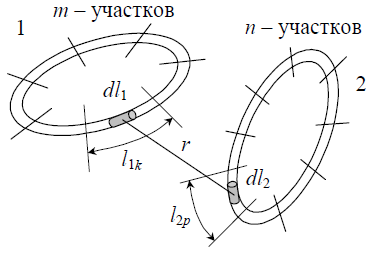
Рис.4.13. Метод участков расчета взаимной индуктивности

Аналогично пооступим при вычислении индуктивности контура. Разобьем контур на m участков (рис.4.14). При этом пусть l_1k есть отрезок участка k по оси проводника, а l_2p - отрезок p участка по внутреннему контуру на поверхности проводника.

Формула для L принимает вид

.

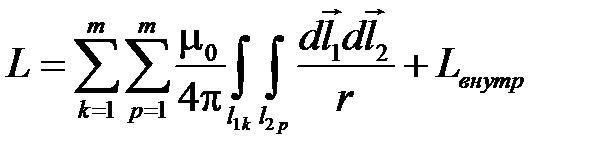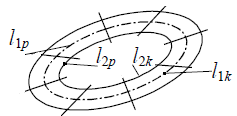
Рис.4.14. Метод участков расчета индуктивности

Выражение под знаком двойной суммы можно условно рассматривать при k=p как внешнюю индуктивность k участка контура и при 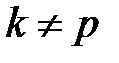- как взаимную индуктивность M_kp между k и p участками контура. При вычислении M_kp можно интегрирование по отрезку внутреннего контура l_2p заменить интегрированием по оси l_1p того же p - участка. Тогда будем иметь

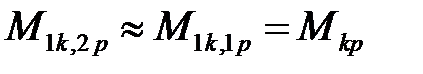и .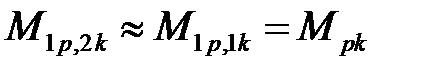

Учитывая, что 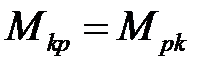, получаем

,

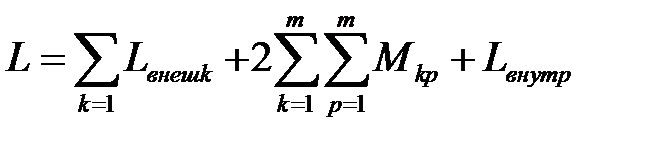где ; ,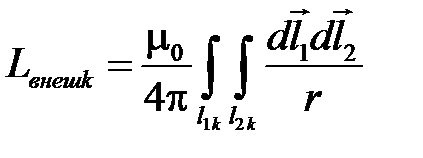

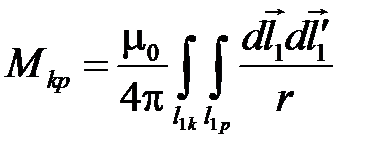причем 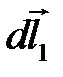-элемент на оси k участка, 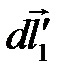-элемент на оси p участка.

В выражении для L во втором члене p¹k и определенное сочетание индексов k и p встречается один раз независимо от порядка, в котором они стоят.