Индуктивность трехфазной линии

В каждом проводе трехфазной линии передачи индуктируется не только ЭДС самоиндукции, обусловленная переменным током в этом проводе, но также и ЭДС взаимной индукции, обусловленная токами в других проводах линии. Рассмотрим трехпроводную линию, т. е. линию, в которой отсутствует нейтральный провод. Обычно активные сопротивления r и индуктивности L одинаковы для всех трех проводов. Однако взаимные индуктивности M₁₂, M₂₃ и M₃₁ между проводами при несимметричном расположении проводов будут отличаться друг от друга.

Если токи в линии изменяются по синусоидальному закону, то можно воспользоваться символическим методом и для падения напряжений в проводах написать выражения:

;

;

.

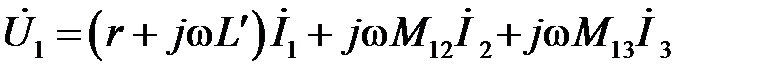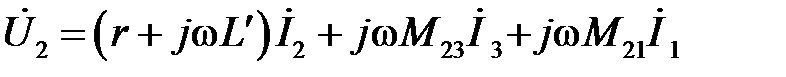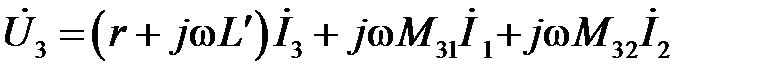Здесь 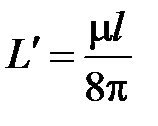— погонная внутренняя индуктивность проводника;

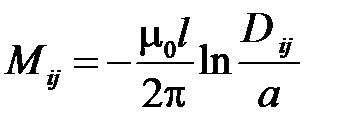— взаимная индуктивность фаз i и j. Здесь знак минус определяется одинаковым направлением токов вдоль линии передачи.

Пусть токи образуют симметричную систему токов прямой последовательности: 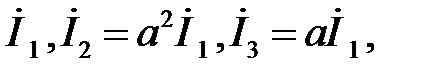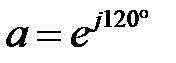. Тогда уравнения можно переписать в виде:

;

; (*)

.

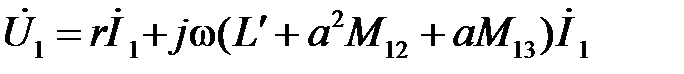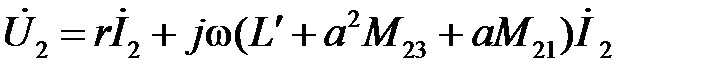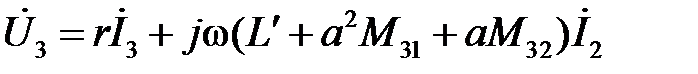Если провода линии расположены симметрично относительно друг друга, тогда 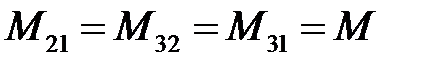. Учитывая, что 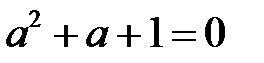, можем записать:

, .

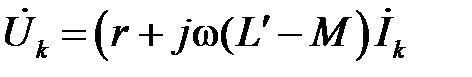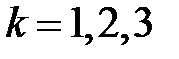Разность 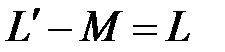в последних уравнениях можно рассматривать как эквивалентную индуктивность одного провода

.

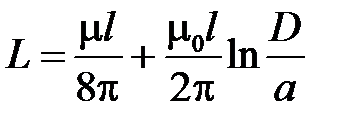При несимметричном расположении проводов расстояния между осями проводов не равны друг другу: .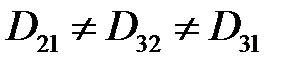

Однако если через равные интервалы вдоль линии осуществлена транспозиция проводов, то выражение для L сохранит свой вид, если под M понимать среднее значение взаимной индуктивности для участка лнии.Тогда индуктивность каждого провода (фазы) трехфазной транспонированной ЛЭП на единицу длины

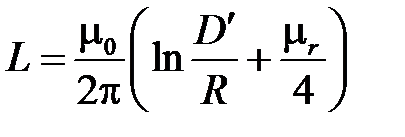[Гн / м],

где .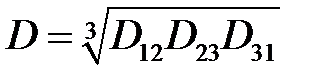

В несимметричной трехфазной линии при прохождении по ней переменного тока имеют место своеобразные энергетические процессы. В уравнениях (*) при 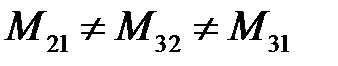выражения, стоящие в круглых скобках, являются комплексными. Их мнимые части после умножения на 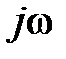дадут вещественные величины, имеющие смысл активных сопротивлений.

Складывая выражения, стоящие в уравнениях (*) в круглых скобках для всех трех фаз, получим при каждой взаимной индуктивности вещественный множитель а² + а = -1. Следовательно, сумма дополнительных активных сопротивлений во всех трех фазах равна нулю, т. е. если в отдельных фазах они положительны, то в других они отрицательны. Иными словами, если из одних фаз энергия отдается, то в другие она поступает в том же количестве, т. е. совершается перенос энергии путем электромагнитной индукции из одной фазы в другую.