Магнитное поле и внутренняя индуктивность прямого провода

Пусть по бесконечно длинному цилиндрическому проводу (рис.4.5)

радиуса R про­текает по­стоянный ток I . Выберем цилиндрическую систему координат 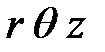так, чтобы ось про­вода совпадала с осью координат z.

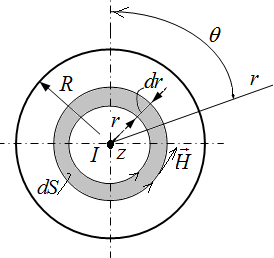
Рис.4.5. Цилиндрический проводник

Имеем две об­ласти, для каж­дой из которых выполним расчёт параметров магнитного поля:

1) область внутри провода при 0 £ r £ R ,

2) область вне провода при R £ r £ ¥ .

Для расчёта поля во внутренней области выберем контур интегрирования в виде ок­ружности с текущим радиусом r<R . Тогда ток внутри контура интег­рирования:

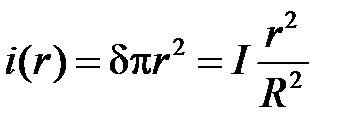, откуда .

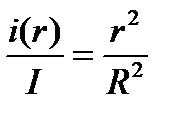Применим к контуру интегрирования закон полного тока в интеграль­ной форме :

,

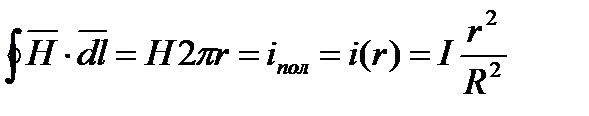откуда следует 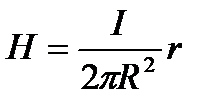и .

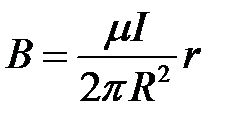Внутренний магнитный поток и внутренняя индуктивность.

Элементарный магнитный поток через элементарную площадку 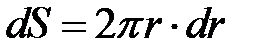на единицу длины провода (рис.4.5) равен

.

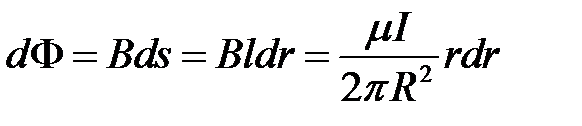Интегрируя по сечению провода, определяем внутренний магнитный поток на единицу длины провода

.

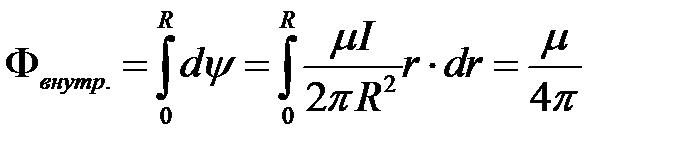Элементарное Векторы 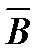и 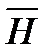направлены по касательной к окружности, их направле­ние опре­деляется по правилу правоходового винта.

При увеличении радиуса на величину dr произойдет приращение магнитного потока на величину 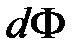на единицу длины провода l=1 и приращение ммагнитногое потокосцепления потокосцепление на величину dy : элементарного потока 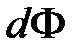на единицу длины провода

.

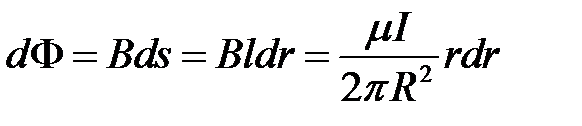
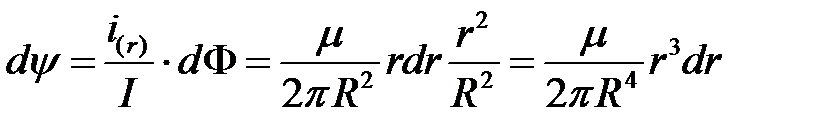Внутренний магнитный поток и внутреннее потокосцепление найдутся в резуль­тате иИнтегрированиуя полученных полученное выше выражений выражение по всему сечению провода, получаем выражение внутреннего потокосцепления:

_,

.

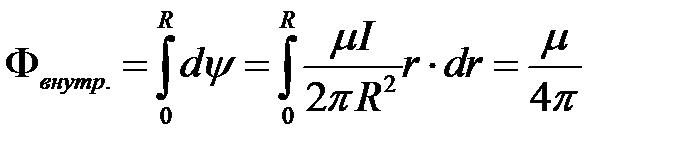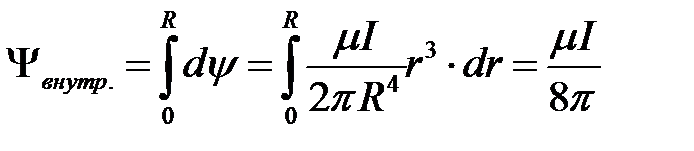Из последнего уравнения следует формула для внутренней индуктив­ности провода на еди­ницу длины провода:

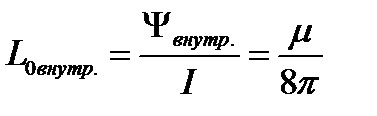[Гн/м].

Внутренняя индуктивность провода зависит от его магнитной проницаемости m (для стальных проводов она значительно больше, чем для медных или алюминиевых) и не зави­сит от его радиуса.

Для расчёта поля во внешней области выберем контур интегрирования в виде окруж­ности с текущим радиусом r>R . Ток внутри контура интегрирова­ния равен I . Из закона полного тока следует:

,

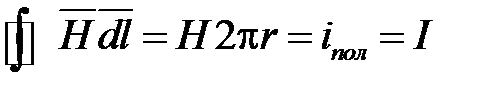откуда

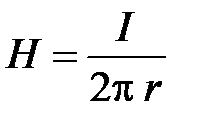и .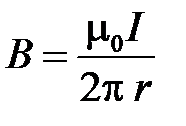

Для магнитного поля снаружи провода можно определить скалярный магнитный потенциал, полагая .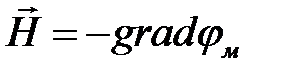

В цилиндрической системе координат

.

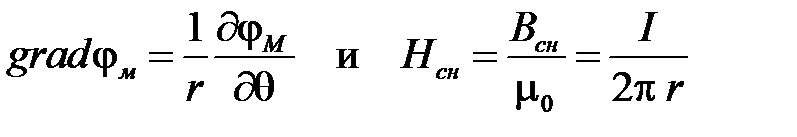Тогда .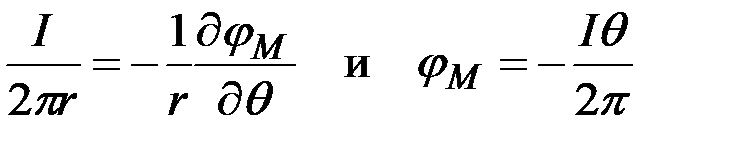

Здесь принято 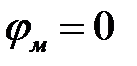при θ = 0.

Определим функцию потока V_м.

.

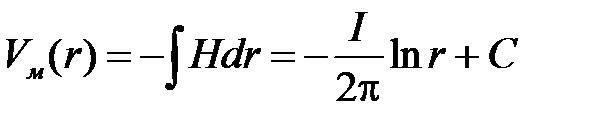Знак минус взят потому, что влево от вектора 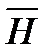координата r, убывает.

Уравнение силовой линии

.

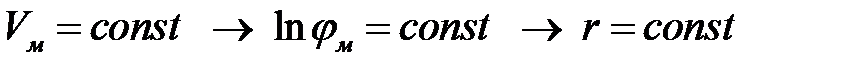Картина поля в приведена на рис.4.6.

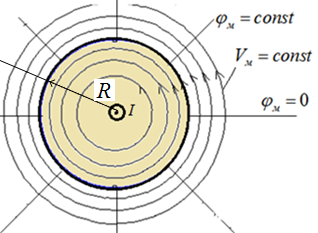
Рис.4.6.Магнитное поле цилиндрического проводника