Скалярный потенциал магнитного поля

В той части пространства, где плотность тока равна нулю, можно представить напряжённость магнитного поля в виде .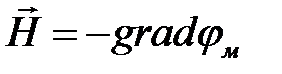

Скалярную функцию 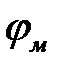называют скалярным магнитным потенциалом. Пользоваться понятием скалярного магнитного потенциала можно только в той области пространства, где плотность тока равна нулю. Однако и в этой части пространства 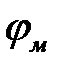является многозначнойфункцией. Линейный интеграл напряженности магнитного поля, взятый по любому замкнутому контуру, не охватывающему контура с током, равен нулю: .

Рис.4.45. К определению скалярного магнитного потенциала

Если же выбрать такой замкнутый путь интегрирования, который охватывает контур тока i, например, путь AlBmA на рис.4.45, то линейный интеграл напряженности магнитного поля по такому пути уже не равен нулю:

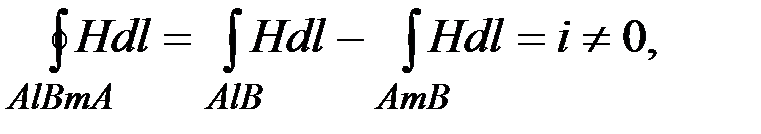
откуда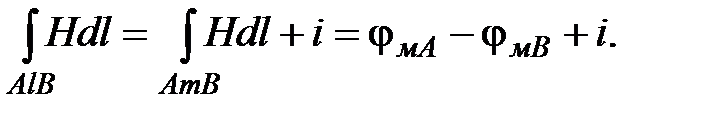

Путь ArBmA охватывает два раза контур с током i. Для такого пути имеем: 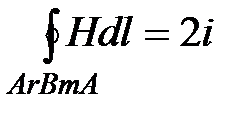и, следовательно, .

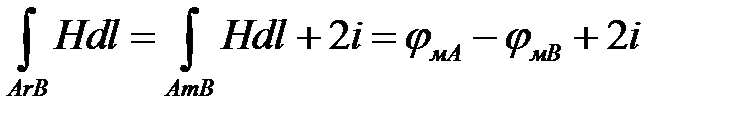Интеграл по некоторому пути AxB может отличаться от интеграла по пути AmB на целое число ki (все пути проходят вне области пространства, занятой самими проводниками с током).

Многозначность скалярного магнитного потенциала не сказывается на определении напряженности магнитного поля,т.к. .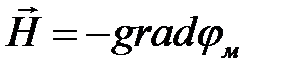

Разность скалярных магнитных потенциалов ― скалярная величина, равная линейному интегралу напряженности магнитного поля между двумя точками вдоль выбранного участка пути, проходящего в односвязной области, где плотность электрического тока равна нулю.

Потенциал скалярный магнитный ―разность скалярных магнитных потенциалов данной точки и другой, определенной, произвольно выбранной.

В соответствии с уравнением в однородной среде 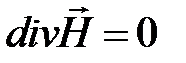и уравнением 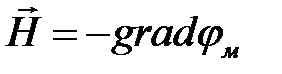скалярный магнитный потенциал подчиняется уравнению Лапласа:

.

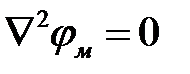Применение понятия скалярного потенциала 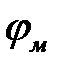в ряде случаев зна­чительно уп­рощает решение задач по расчёту магнитного поля вне токов. Скалярный магнитный потенциал не имеет физического смысла, он служит удобной математической величиной для расчёта магнитного поля.