Алгоритм решения транспортной задачи методом потенциалов
Порядок решения транспортных задач методом потенциалов следующий:
1. Проверяют выполнение необходимого и достаточного условия разрешимости задачи. Если задача имеет неправильный баланс, то вводят фиктивного поставщика или потребителя с недостающими запасами или запросами и нулевыми стоимостями перевозок.
2. Строят начальное опорное решение (методом минимальной стоимости или каким-либо другим методом) и проверяют правильность его построения, для чего подсчитывают количество занятых клеток (их должно быть m + n -1) и убеждаются в линейной независимости векторов-условий (методом вычеркивания).
3. Строят систему потенциалов, соответствующих опорному решению. Для этого решают систему уравнений
 при
при  .
.
Для того чтобы найти частное решение системы одному из потенциалов (обычно тому, которому соответствует большее число занятых клеток) задают произвольно некоторое значение (чаще нуль). Остальные потенциалы однозначно определяют по формулам
 при
при  , (6.24)
, (6.24)
если известен потенциал  , и
, и
 при
при  , (6.25)
, (6.25)
если известен потенциал  .
.
4. Проверяют, выполняется ли условие оптимальности для свободных клеток таблицы. Для этого вычисляют оценки для всех свободных клеток по формуле

и те из них, которые больше нуля, записывают в левые нижние углы клеток. Если для всех свободных клеток  , то решение является оптимальным, вычисляют значение целевой функции и решение задачи заканчивается. Если же имеется хотя бы одна клетка с положительной оценкой, то опорное решение не является оптимальным.
, то решение является оптимальным, вычисляют значение целевой функции и решение задачи заканчивается. Если же имеется хотя бы одна клетка с положительной оценкой, то опорное решение не является оптимальным.
5. Переходят к новому опорному решению, на котором значение целевой функции будет меньше. Для этого находят клетку таблицы задачи, которой соответствует наибольшая положительная оценка
 .
.
Строят цикл, включающий в свой состав данную клетку и часть клеток, занятых опорным решением. В клетках цикла расставляют поочередно знаки "+" и "-", начиная с "+" в клетке с наибольшей положительной оценкой. Осуществляют сдвиг (перераспределение груза) по циклу на величину  . Клетка со знаком "-", в которой достигается
. Клетка со знаком "-", в которой достигается  остается пустой. Если минимум достигается в нескольких клетках, то одна из них остается пустой, а в остальных проставляют базисные нули, чтобы число занятых клеток оставалось равным m + n - 1.
остается пустой. Если минимум достигается в нескольких клетках, то одна из них остается пустой, а в остальных проставляют базисные нули, чтобы число занятых клеток оставалось равным m + n - 1.
Далее возвращаются к пункту 3 алгоритма.
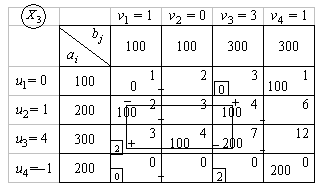
Пример 6.5. Решить транспортную задачу, исходные данные которой приведены в табл. 6.13.
Т а б л и ц а 6.13
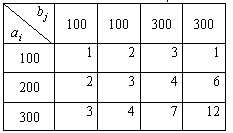
Решение. 1. Проверяем выполнение необходимого и достаточного условия разрешимости задачи. Находим суммарные запасы поставщиков и запросы потребителей
 ,
,  .
.
Задача с неправильным балансом. Вводим четвертого, фиктивного поставщика с запасами  = 800 – 600 = 200 и нулевыми стоимостями перевозки единиц груза (табл. 6.14).
= 800 – 600 = 200 и нулевыми стоимостями перевозки единиц груза (табл. 6.14).
2. Составляем начальное опорное решение методом минимальной стоимости (табл. 6.14).
Т а б л и ц а 6.14
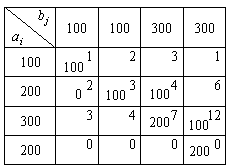
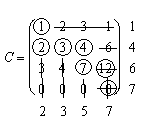
Записываем матрицу стоимостей С. Находим в этой матрице наименьшие на каждом шаге стоимости и направляем в клетку, которая соответствует этим стоимостям, максимально допустимые объемы перевозок грузов.
При этом исключаем на каждом шаге одного поставщика или потребителя. Кружочками в матрице С указаны минимальные элементы, а цифрами рядом со строками и столбцами - порядок исключения из рассмотрения поставщиков и потребителей. Напомним, что запасы фиктивного поставщика вывозятся в последнюю очередь.
Полученное решение  имеет m + n - 1 = 4 + 4 -1 = 7 базисных переменных. Опорное решение является вырожденным, так как одна из его координат равна нулю. Вычислим значение целевой функции на этом опорном решении
имеет m + n - 1 = 4 + 4 -1 = 7 базисных переменных. Опорное решение является вырожденным, так как одна из его координат равна нулю. Вычислим значение целевой функции на этом опорном решении  = 100 × 1 + 0 × 2 + 100 × 3 + 100 × 4 + 200 × 7 + 100 × 12 + 200 × 0 = 3400.
= 100 × 1 + 0 × 2 + 100 × 3 + 100 × 4 + 200 × 7 + 100 × 12 + 200 × 0 = 3400.
3. Для проверки оптимальности опорного решения необходимо найти потенциалы. По признаку оптимальности в каждой занятой опорным решением клетке таблицы транспортной задачи сумма потенциалов равняется стоимости (  при
при  ). Записываем систему уравнений для нахождения потенциалов
). Записываем систему уравнений для нахождения потенциалов
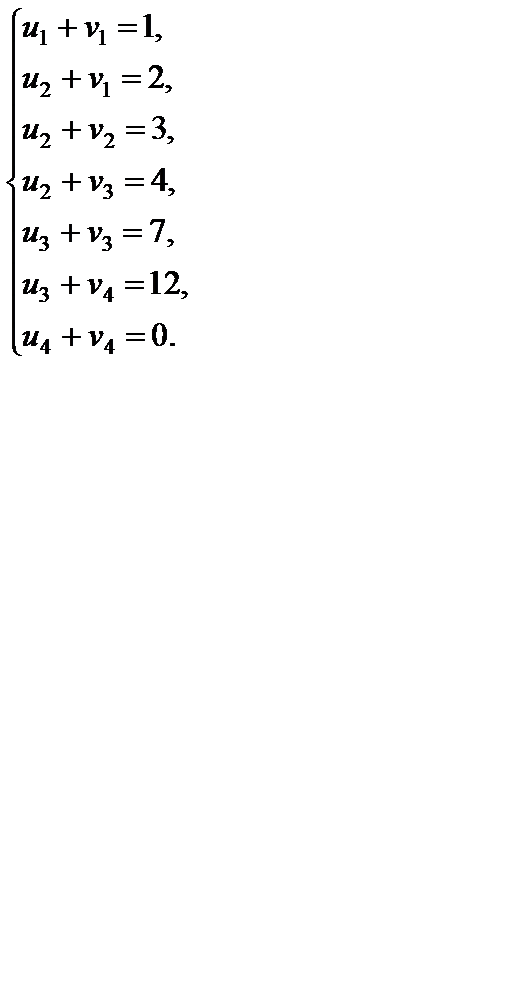
Система состоит из семи уравнений и имеет восемь переменных. Система неопределенная. Одному из потенциалов задаем значение произвольно: пусть  = 0. Остальные потенциалы находятся однозначно
= 0. Остальные потенциалы находятся однозначно
 = 0;
= 0;
 = 2 – 0 = 2;
= 2 – 0 = 2;
 = 3 – 0 = 3;
= 3 – 0 = 3;
 = 4 – 0 = 4;
= 4 – 0 = 4;
 = 1 – 2 = –1;
= 1 – 2 = –1;
 = 7 – 4 = 3;
= 7 – 4 = 3;
 = 12 – 3 = 9;
= 12 – 3 = 9;
 = 0 – 9 = – 9.
= 0 – 9 = – 9.
Значения потенциалов записываем рядом с запасами или запросами соответствующих поставщиков и потребителей в таблицу
(табл. 6.15).
Система уравнений для нахождения потенциалов достаточно проста, обычно ее решают устно, глядя на таблицу задачи, ее занятые клетки и известные потенциалы. Любой неизвестный потенциал, соответствующий занятой клетке, равен находящейся в этой клетке стоимости, минус известный потенциал, соответствующий этой же клетке (6.24), (6.25).
Т а б л и ц а 6.15
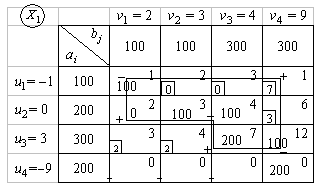
4. Проверяем опорное решение  на оптимальность. С этой целью вычисляем оценки
на оптимальность. С этой целью вычисляем оценки  для всех незаполненных клеток таблицы (для всех занятых клеток
для всех незаполненных клеток таблицы (для всех занятых клеток  = 0)
= 0)








 .
.
Положительные оценки записывают в левые нижние углы соответствующих клеток таблицы, вместо отрицательных просто ставим знак "–".
Начальное опорное решение не является оптимальным, так как имеются положительные оценки.
5. Переходим к новому опорному решению. Находим клетку таблицы, которой соответствует наибольшая положительная оценка. Имеем  max {7, 3, 2, 2} =7 для клетки (1, 4). Для этой клетки строим цикл. Ставим в нее знак "+", присоединяем ее к занятым клеткам и применяем метод вычеркивания. После проведения вычеркиваний в таблице остаются только образующие цикл клетки. Цикл изображен в табл. 6.15. На основании теоремы 6.6 такой цикл единственный. В угловых точках цикла расставляются поочередно знаки "+" и "-", начиная с "+" в клетке (1, 4). В клетки, отмеченные знаком "+" добавляется груз q, а из клеток, отмеченных знаком минус, вычитается такой же по величине груз. Определяем величину груза q, перераспределяемого по циклу. Она равняется значению наименьшей из перевозок в клетках цикла, отмеченных знаком "–"
max {7, 3, 2, 2} =7 для клетки (1, 4). Для этой клетки строим цикл. Ставим в нее знак "+", присоединяем ее к занятым клеткам и применяем метод вычеркивания. После проведения вычеркиваний в таблице остаются только образующие цикл клетки. Цикл изображен в табл. 6.15. На основании теоремы 6.6 такой цикл единственный. В угловых точках цикла расставляются поочередно знаки "+" и "-", начиная с "+" в клетке (1, 4). В клетки, отмеченные знаком "+" добавляется груз q, а из клеток, отмеченных знаком минус, вычитается такой же по величине груз. Определяем величину груза q, перераспределяемого по циклу. Она равняется значению наименьшей из перевозок в клетках цикла, отмеченных знаком "–"  {100, 100, 100} = 100. Осуществляем сдвиг по циклу на величину q = 100. Получаем второе опорное решение
{100, 100, 100} = 100. Осуществляем сдвиг по циклу на величину q = 100. Получаем второе опорное решение  (табл. 6.16). Т а б л и ц а 6.16
(табл. 6.16). Т а б л и ц а 6.16
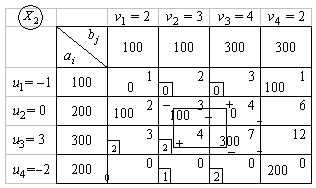
В данном случае минимум перевозок в клетках, отмеченных знаком "–" достигался сразу в трех клетках, поэтому для того, чтобы число занятых клеток опорного решения было по-прежнему равно
m + n - 1 = 7, в клетки с номерами (1, 1) и (2, 3) поставлены нулевые базисные перевозки. Следует освобождать клетку с большей стоимостью перевозки, т. е. клетку (3, 4).
Вычисляем значение целевой функции на втором опорном решении
 = 0 × 1 + 100 × 1 + 100 × 2 + 100 × 3 + 0 × 4 + 300 × 7 + 200 × 0 = 2700.
= 0 × 1 + 100 × 1 + 100 × 2 + 100 × 3 + 0 × 4 + 300 × 7 + 200 × 0 = 2700.
6. Проверяем второе опорное решение  на оптимальность. Находим потенциалы и оценки. Они приведены в табл. 6.16. Решение не является оптимальным, так как имеются положительные оценки
на оптимальность. Находим потенциалы и оценки. Они приведены в табл. 6.16. Решение не является оптимальным, так как имеются положительные оценки 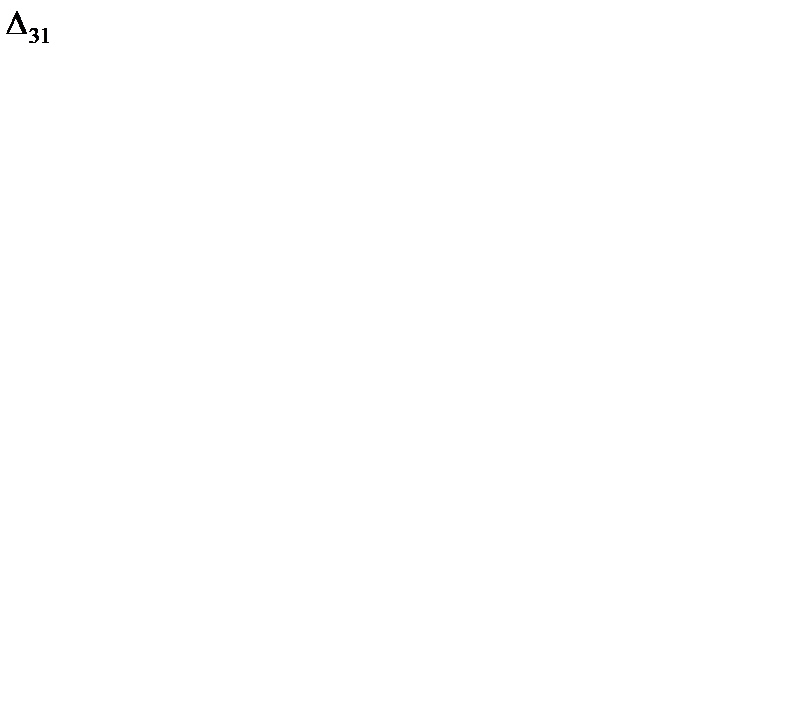 = 2,
= 2, 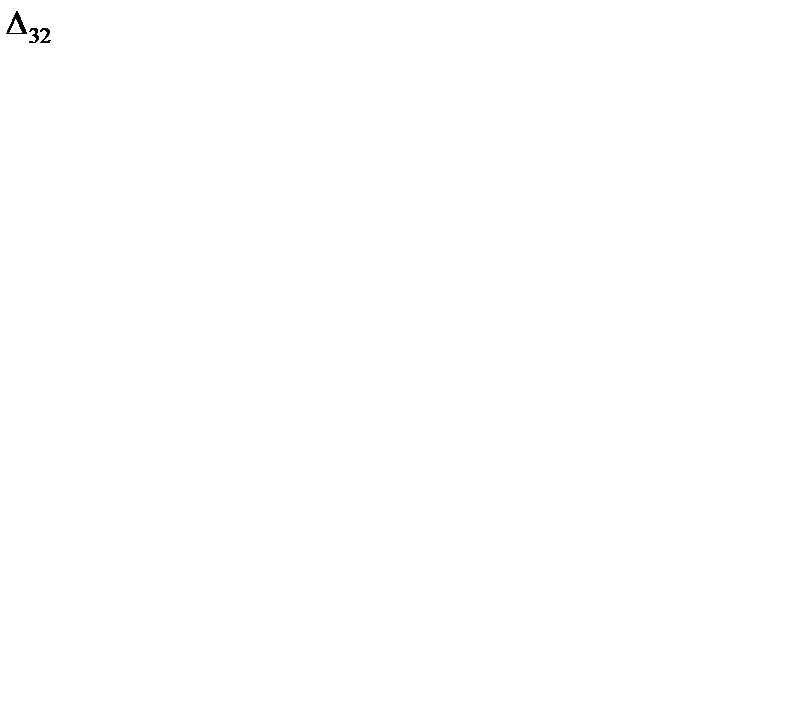 = 2,
= 2,  = 1 и
= 1 и 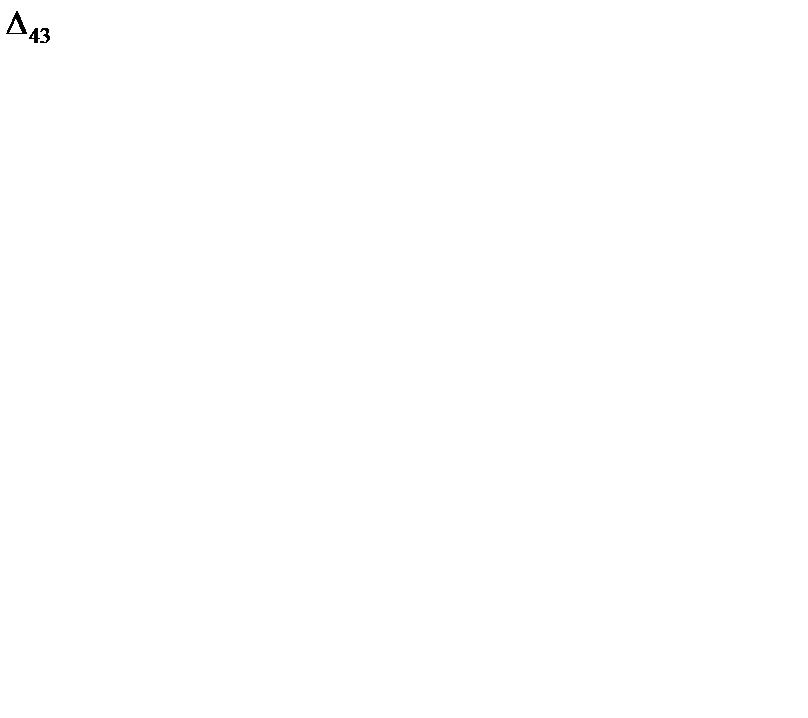 = 2. Наибольшая из них равняется 2 одновременно для трех клеток (3, 1), (3, 2), (4, 3). В одну из них, пусть в клетку (3, 2), ставим знак "+". Для этой клетки строим цикл
= 2. Наибольшая из них равняется 2 одновременно для трех клеток (3, 1), (3, 2), (4, 3). В одну из них, пусть в клетку (3, 2), ставим знак "+". Для этой клетки строим цикл
(табл. 6.16), и находим величину груза для перераспределения по циклу:  {100, 300} = 100. Осуществляем сдвиг по циклу на величину q = 100. Получаем третье опорное решение
{100, 300} = 100. Осуществляем сдвиг по циклу на величину q = 100. Получаем третье опорное решение 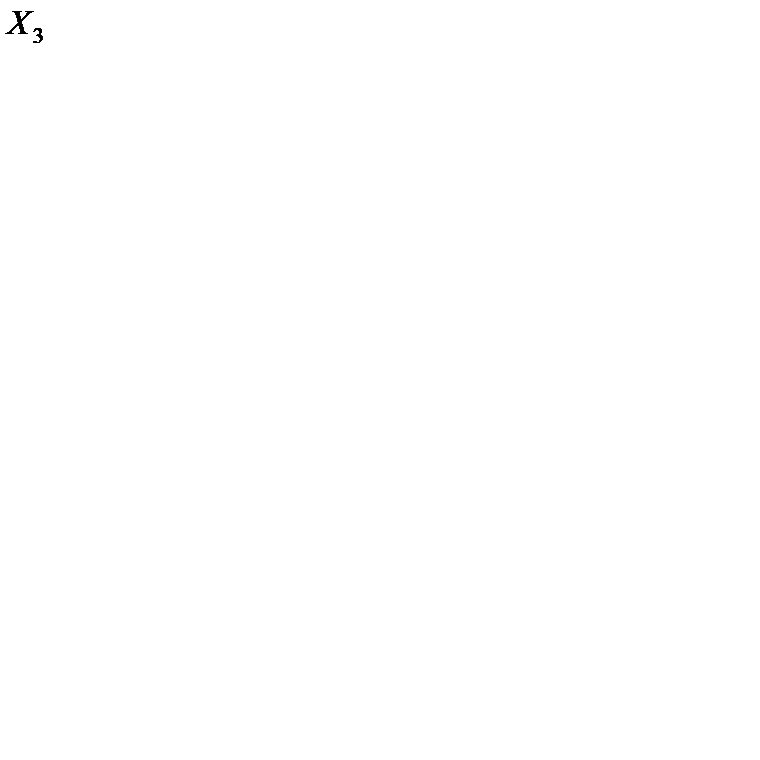 (табл. 6.17).
(табл. 6.17).
Т а б л и ц а 6.17
Вычисляем значение целевой функции на третьем опорном решении.
 = 0×1 + 100×1 + 100×2 + 100×4 + 100×4 + 200×7 + 200×0 = 2500.
= 0×1 + 100×1 + 100×2 + 100×4 + 100×4 + 200×7 + 200×0 = 2500.
7. Проверяем третье опорное решение на оптимальность. Находим потенциалы и оценки. Они приведены в табл. 6.17. Решение не является оптимальным, так как имеются положительные оценки 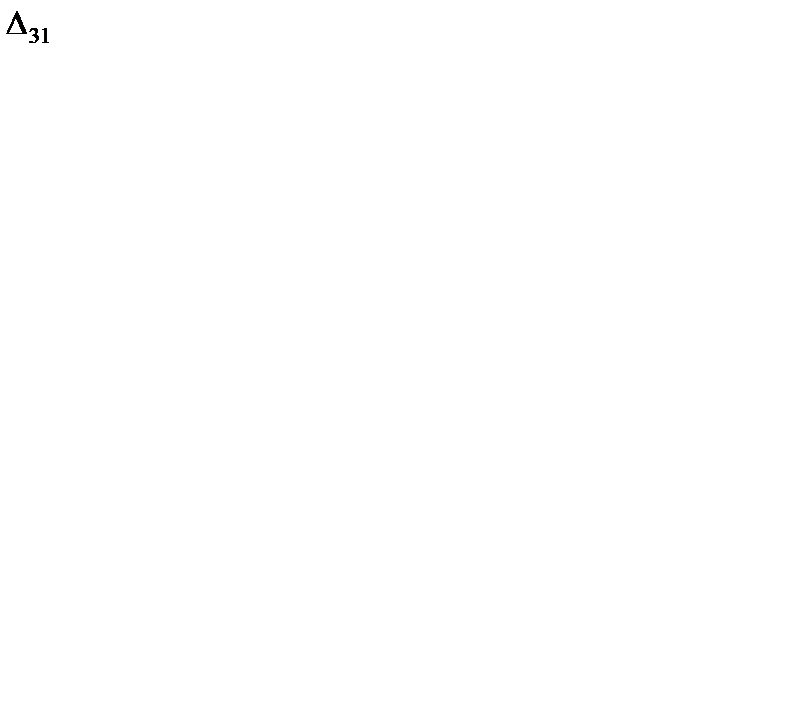 = 2 и
= 2 и 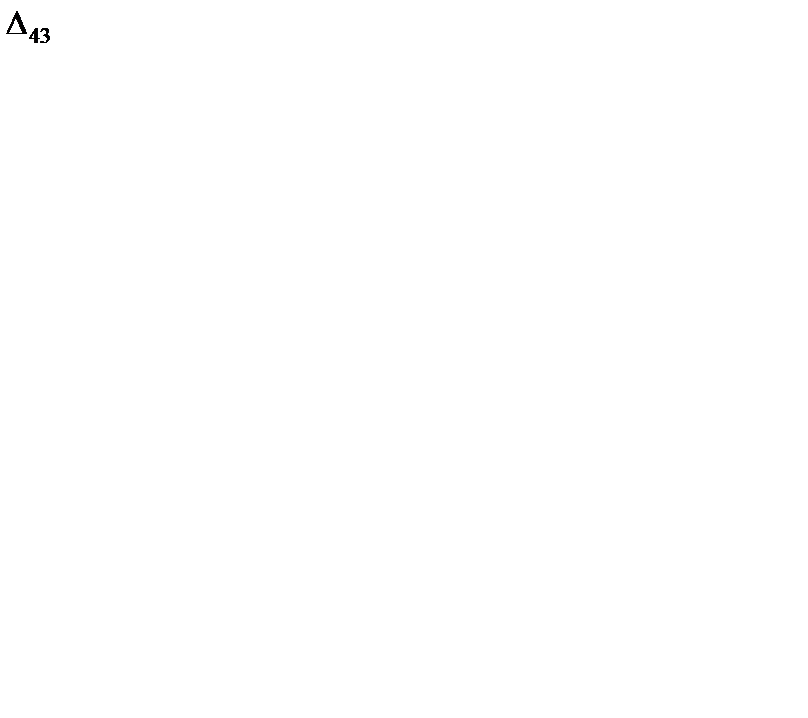 = 2. В одну из клеток с положительной оценкой, пусть в клетку (3, 1), ставим знак "+". Для этой клетки строим цикл (см. табл. 6.17) и находим величину груза для перераспределения по циклу
= 2. В одну из клеток с положительной оценкой, пусть в клетку (3, 1), ставим знак "+". Для этой клетки строим цикл (см. табл. 6.17) и находим величину груза для перераспределения по циклу  {100, 200} = 100. Осуществляем сдвиг по циклу на величину q = 100. Получаем четвертое опорное решение
{100, 200} = 100. Осуществляем сдвиг по циклу на величину q = 100. Получаем четвертое опорное решение 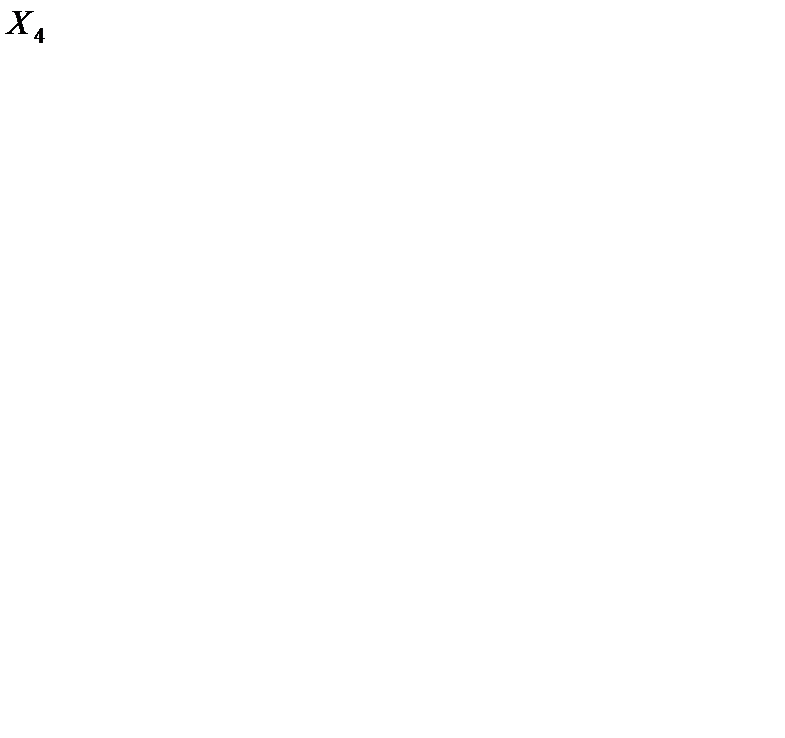 (табл. 6.18).
(табл. 6.18).
Таблица 6.18
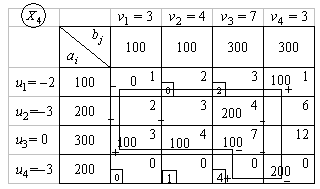
Вычисляем значение целевой функции на четвертом опорном решении  = 0×1 + 100×1 + 200×4 + 100×3 + 100×4 + 100×7 + 200×0 = 2300.
= 0×1 + 100×1 + 200×4 + 100×3 + 100×4 + 100×7 + 200×0 = 2300.
8. Проверяем решение 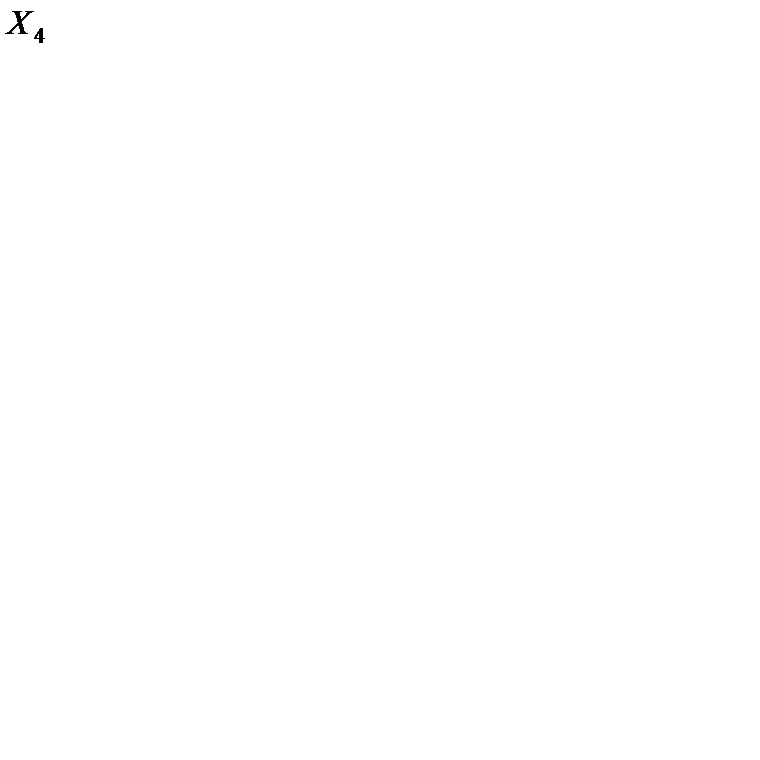 на оптимальность. Находим потенциалы и оценки. Они приведены в табл. 6.18. Положительными являются оценки
на оптимальность. Находим потенциалы и оценки. Они приведены в табл. 6.18. Положительными являются оценки  = 2,
= 2,  = 1 и
= 1 и  = 4. Для клетки (4, 3), которой соответствует наибольшая оценка, строим цикл (табл. 6.18) и находим величину груза для перераспределения по циклу
= 4. Для клетки (4, 3), которой соответствует наибольшая оценка, строим цикл (табл. 6.18) и находим величину груза для перераспределения по циклу  {200, 0,
{200, 0,
100} = 0. Осуществляем сдвиг по циклу на величину q = 0. Получаем пятое опорное решение 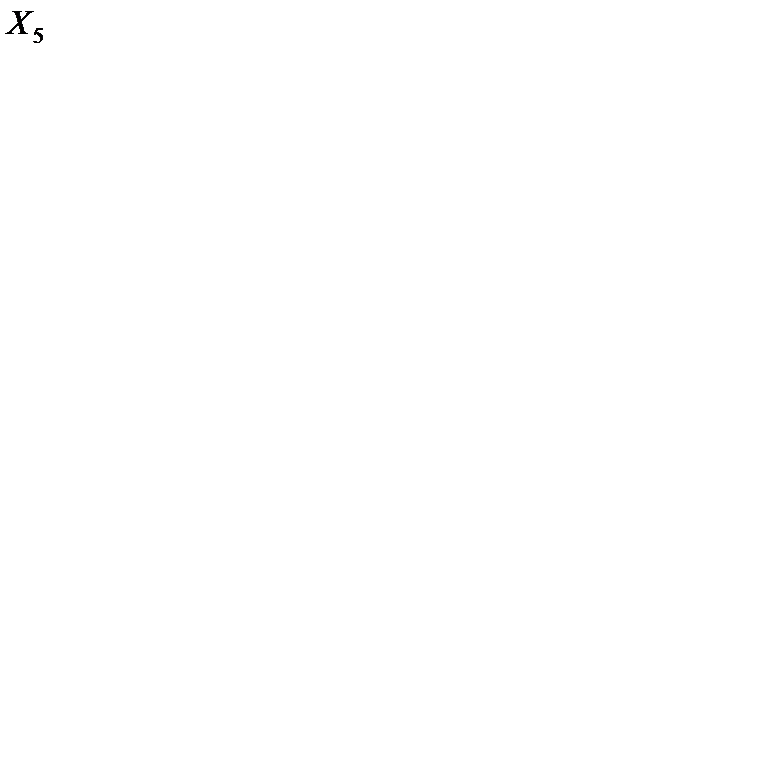 (табл. 6.19).
(табл. 6.19).
Т а б л и ц а 6.19
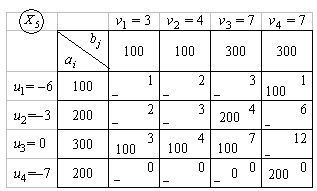
Решение является оптимальным, так как все оценки отрицательные. Значение целевой функции  =
=  = 2300.
= 2300.
Ответ: minZ(X) = 2300 при 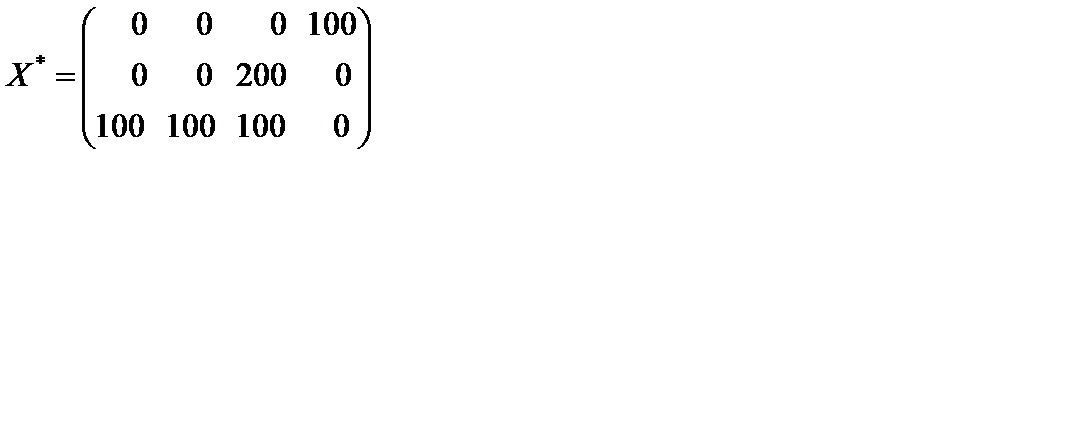 .
.
Дата добавления: 2017-05-18; просмотров: 1482;
