Лекция №12 МЕТОД ГОМОРИ РЕШЕНИЯ ЗАДАЧ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ

В общем случае задача целочисленного программирования формулируется следующим образом.

Найти максимум или минимум функции

(7.1)

при условиях

, i = 1, 2, ..., m, (7.2)

, j = 1, 2, …, n, (7.3)

, j = 1, 2, ..., n - целые числа. (7.4)

Согласно методу Р. Е. Гомори сначала решают задачу линейного программирования симплексным методом без учета целочисленности переменных. Если оптимальное решение будет целочисленным, то решение задачи заканчивается. Если же оптимальное решение оказывается нецелочисленным, то изменяют область допустимых решений задачи так, чтобы ее угловые точки имели целочисленные координаты. Ввиду того, что в результате этого область допустимых решений уменьшается, данный метод часто называют методом отсечений. На основе одного из уравнений системы ограничений составляют дополнительное ограничение, которое отсекает от области допустимых решений нецелочисленное оптимальное решение, но при этом сохраняет целочисленные вершины этой области.

Рассмотрим способ составления дополнительного ограничения.

Введем понятие целой и дробной части числа. Число называется целой частью числа , если оно наиболее близкое к нему целое и не превосходит . Дробная часть числа находится как разность этого числа и его целой части, т. е. . Например, для числа 7/4 целая часть , дробная часть равна . Для числа –9/5 целая часть , дробная часть равна –9/5 – (–2) = 1/5. Дробная часть числа всегда неотрицательна и меньше единицы.

Пусть с помощью симплексного метода получено оптимальное решение задачи, которое не является целочисленным, и его координата является дробным числом. Пусть соответствующее этой координате уравнение-ограничение в последней симплексной таблице имеет вид

, (7.5)

где - базисная переменная в уравнении, - свободные переменные в системе уравнений, - правая часть уравнения (координата оптимального решения), - коэффициенты при неизвестных (коэффициенты разложений векторов условий по базису опорного решения).

Из уравнения (7.5) найдем .

Представим и в виде сумм целых и дробных частей

, .

Подставим эти выражения в последнее равенство

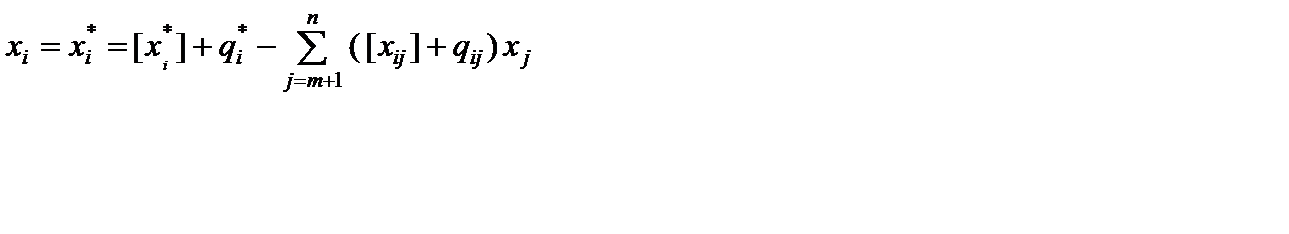Û .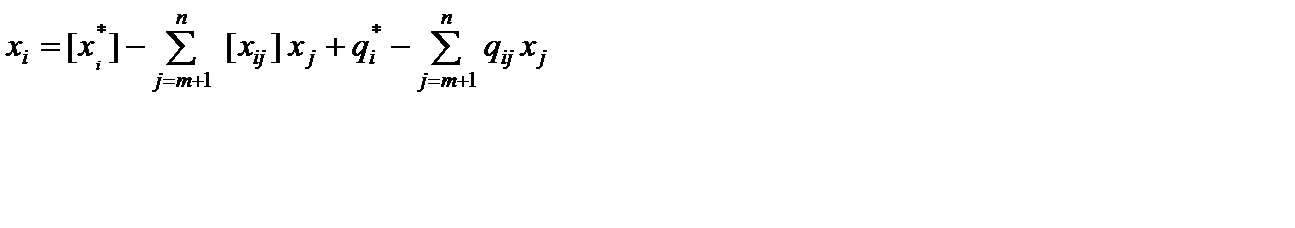

Пусть свободные переменные (j = m + 1, m + 2, …, n) являются целыми. Тогда разность будет целым числом и для того, чтобы базисная переменная была целой, должна быть целой также разность

. (7.6)

Ввиду того, что и для любого дробная часть неотрицательная , то . Так как , то разность (7.6) может быть только целой отрицательной или равной нулю, т. е.

. (7.7)

Это и является дополнительным ограничением. В неравенство (7.7) вводят дополнительную переменную , получают уравнение

. (7.8)

В систему ограничений задачи это ограничение записывают в виде

. (7.9)

После этого решение задачи продолжают двойственным симплексным методом. Если в результате получается целочисленное решение, то процесс решения заканчивается, в противном случае составляют дополнительное ограничение.

Задача не имеет целочисленного решения, если оптимальное решение имеет координату с дробной частью и все коэффициенты соответствующего уравнения являются целыми.

Пример 7.1. Найти оптимальное целочисленное решение задачи

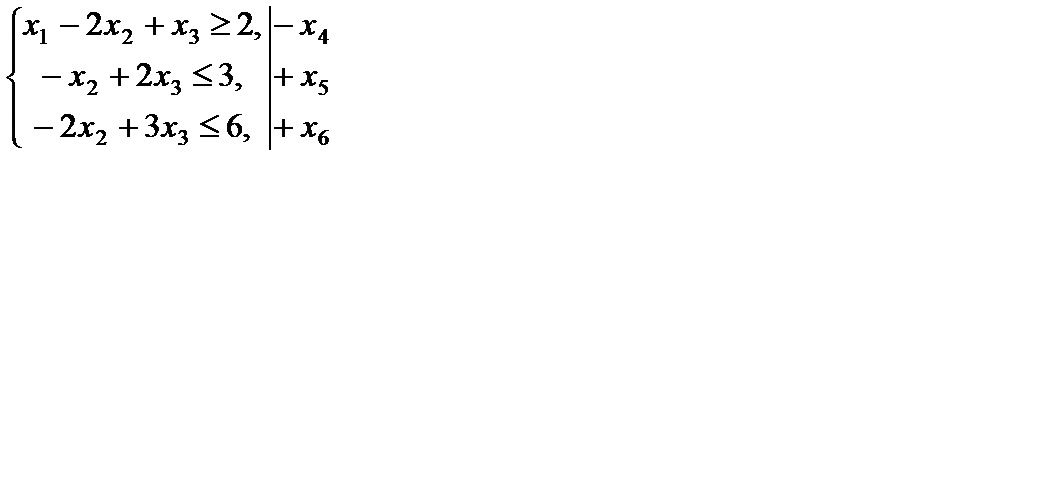
– целые, j = 1, 2, 3.

Приводим задачу к каноническому виду с помощью дополнительных переменных , получаем

,

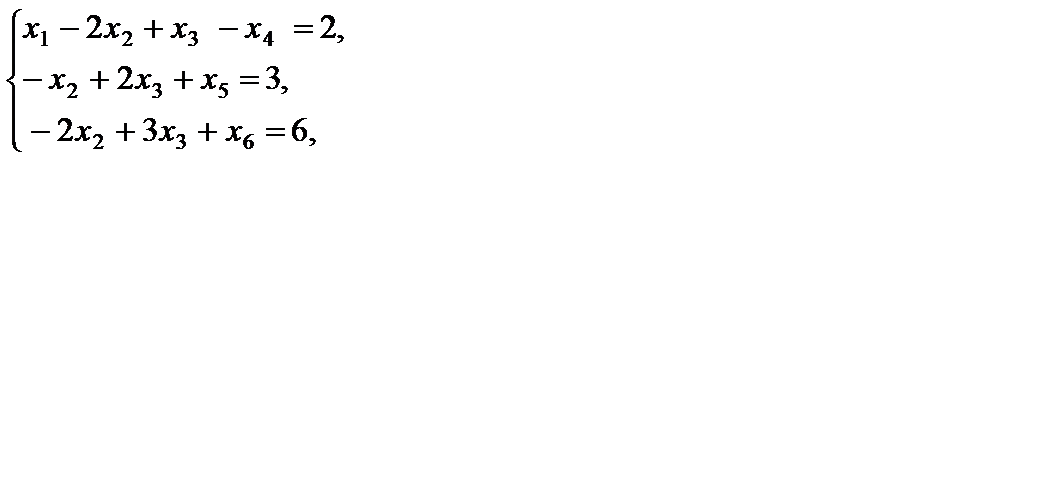
– целые, j = 1, 2, 3, 4, 5, 6.

Данная задача имеет начальное опорное решение 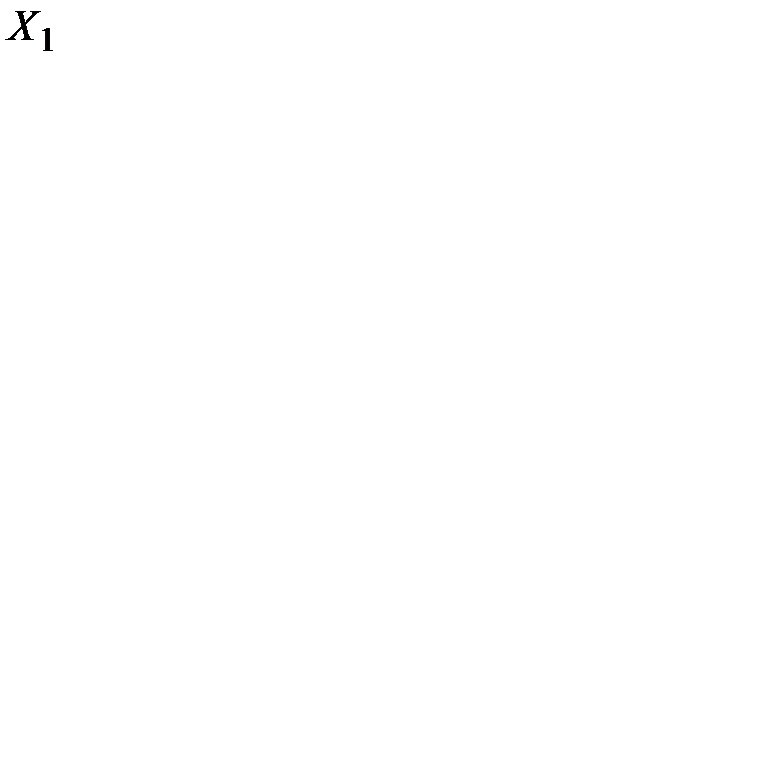= (2, 0, 0, 0, 3, 6) с единичным базисом . Вычисления приведены в табл. 7.1.

Т а б л и ц а 7.1

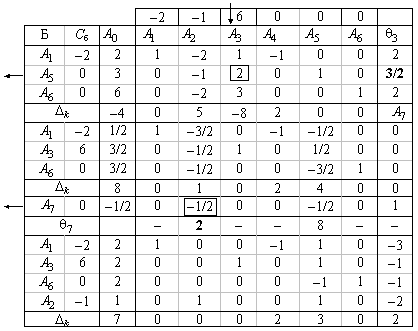
Записываем опорное решение в симплексную таблицу и вычисляем оценки разложений векторов условий по базису этого решения. Данное решение не является оптимальным, так как в задаче на максимум для вектора оценка = -8 < 0. Вводим в базис опорного решения вектор вместо вектора . Получаем нецелочисленное оптимальное решение 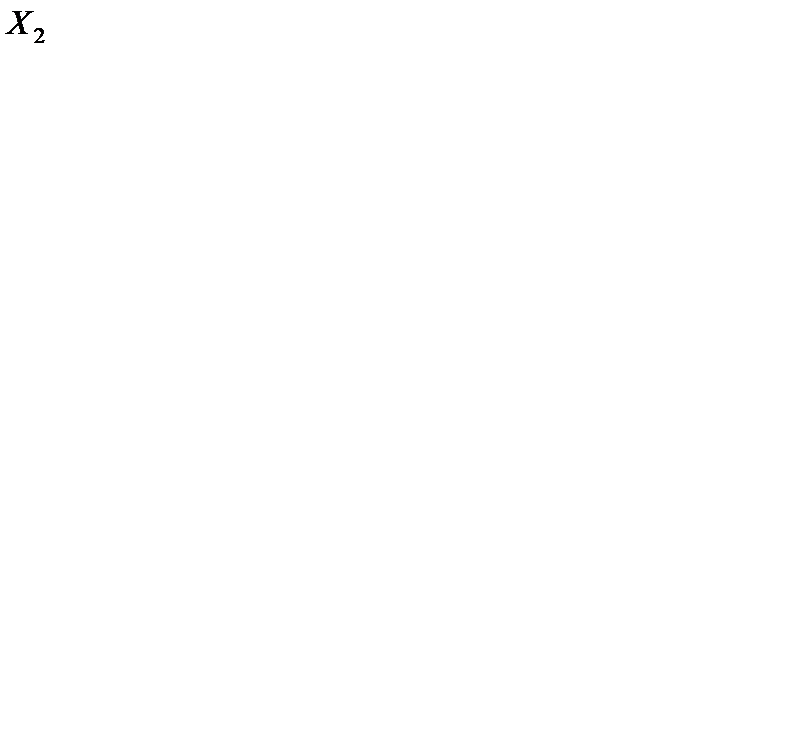= (1/2, 0, 3/2, 0, 0, 3/2). Составляем дополнительное ограничение вида (7.9). Для этого используем ограничение, у которого правая часть имеет большую дробную часть. Находим дробные части правых частей уравнений (координат опорного решения): 1/2 – 0 = 1/2; 3/2 – 1 = 1/2. Так как они равны между собой, для составления дополнительного ограничения используем по своему усмотрению первое уравнение. Находим дробные части коэффициентов этого уравнения:

1 – 1 = 0; –3/2 - (–2) =1/2, 0 – 0 = 0; –1 – (–1) = 0; –1/2 – (–1) = 1/2.

Составляем дополнительное ограничение

.

Это уравнение записано в таблицу после строки оценок. Оно имеет разрешенную неизвестную , которую включаем в число базисных неизвестных. В результате этого опорное решение 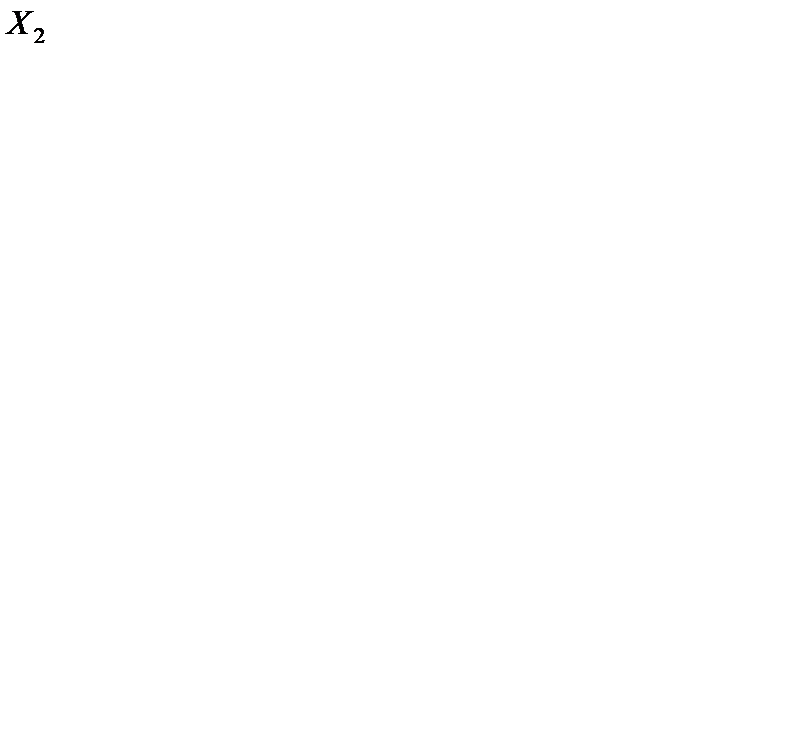превращается в почти допустимое опорное решение 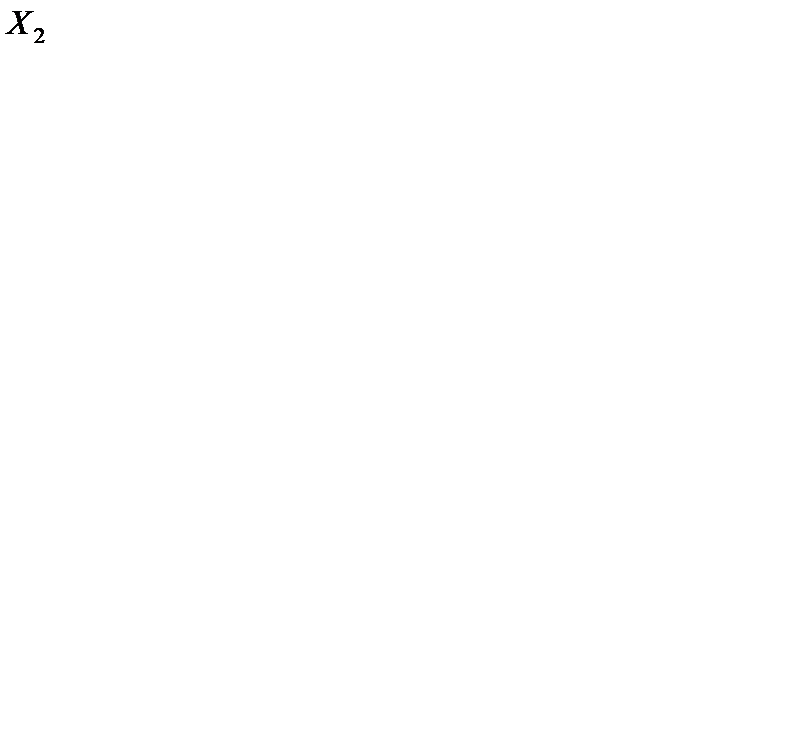= (1/2, 0, 3/2, 0, 0, 3/2, -1/2). Введение вектора в базис не приводит к изменению оценок. В задаче на максимум все оценки неотрицательные, выполняются условия для применения двойственного симплексного метода. Теперь вектор необходимо вывести из базиса, так как дополнительное ограничение имеет в правой части отрицательную величину. С помощью параметра , вычисляемого по формуле (гл. 5)

, ,

находится вектор , вводимый в базис. В результате преобразования Жордана с разрешающим элементом -1/2 при получается новое опорное решение 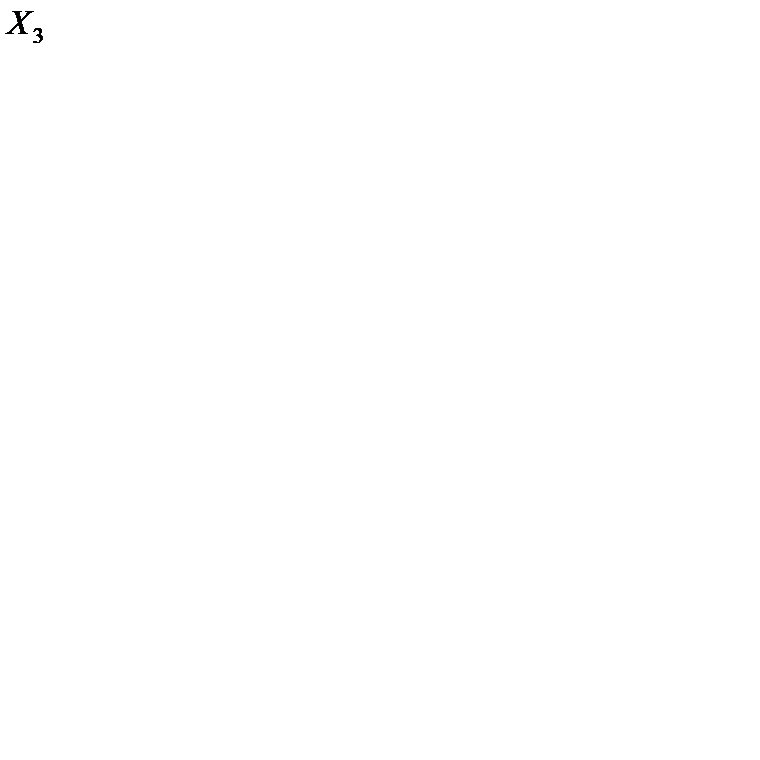= (2, 1, 2, 0, 0, 2, 0), координаты которого являются целыми. Следовательно, это решение будет оптимальным.

Ответ: max Z(X_ц) = 7 при X_ц = (2, 1, 2).

Лекция №13

ОБЩАЯ ЗАДАЧА НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Источники нелинейности относятся в основном к одной из двух категорий:

1) реально существующие и эмпирически наблюдаемые нелинейные соотношения, например: непропорциональные зависимости между объемом производства и затратами; между количеством используемого в производстве компонента и некоторыми показателями качества готовой продукции; между затратами сырья и физическими параметрами (давление, температура и т.п.) соответствующего производственного процесса; между выручкой и объемом реализации и др.;

2) установленные (постулируемые) руководством правила поведения или задаваемые зависимости, например: формулы или правила расчета с потребителями энергии или других видов услуг; эвристические правила определения страховых уровней запаса продукции; гипотезы о характере вероятностного распределения рассматриваемых в модели случайных величин; различного рода договорные условия взаимодействия между партнерами по бизнесу и др.

Решать линейные задачи значительно проще, чем нелинейные, и если линейная модель обеспечивает адекватность реальным ситуациям, то ее и следует использовать. В практике экономического управления модели линейного программирования успешно применялись даже в условиях нелинейности. В одних случаях нелинейность была несущественной и ею можно было пренебречь, в других — производилась линеаризация нелинейных соотношений или применялись специальные приемы, например строились так называемые линейные аппроксимационные модели, благодаря чему достигалась требуемая адекватность. Тем не менее имеется большое число ситуаций, где нелинейность является существенной и ее нужно учитывать в явном виде.

Далее приводятся общая модель задачи нелинейного программирования и классы задач НЛП, а также описываются условия оптимальности решения.

Модели

В общем виде задача НЛП описывается с помощью следующей модели нелинейного программирования:

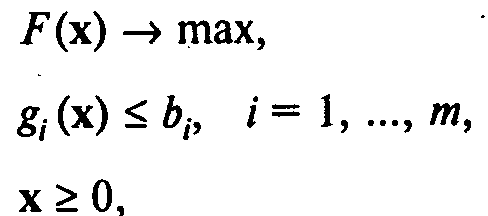
где х = (x1, х2, ..., хn) — вектор переменных задачи.

Задача (1)—(3) называется задачей нелинейного программирования в стандартной форме на максимум.

Может быть сформулирована также задача НЛП на минимум.

Вектор х = (x1, х2, ..., хn), компоненты хj которого удовлетворяют ограничениям (2) и (3), называется допустимым решением или допустимым планом задачи НЛП.

Совокупность всех допустимых планов называется множеством допустимых планов.

Допустимое решение задачи НЛП, на котором целевая функция (1) достигает максимального значения, называется оптимальным решением задачи НЛП.

Возможное местонахождение максимального значения функции F(x) при наличии ограничений (2) и (3) определяется следующим общим принципом. Максимальное значение F(x), если оно существует, может достигаться в одной или более точках, которые могут принадлежать следующим множествам:

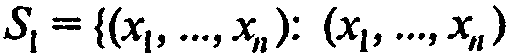нутренняя точка множества допустимых планов, в которой все первые частные производные

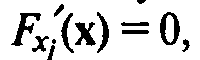
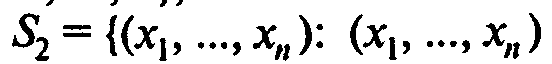
— точка границы множества допустимых планов};

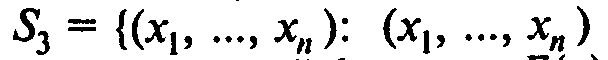— точка множества допустимых планов, в которой функция F(x) недифференцируема}.

В отличие от задач линейного программирования, любая из которых может быть решена симплекс-методом, не существует одного или нескольких алгоритмов, эффективных для решения любых нелинейных задач. Какой-то алгоритм может оказаться чрезвычайно эффективным для решения задач одного типа и неудачным для задач другого типа.

Эффективность алгоритма может даже существенно зависеть от постановки задачи, например от изменения масштабов измерения тех или иных переменных. Поэтому алгоритмы разрабатываются для каждого класса (типа) задач. Программы, ориентированные на решение определенного класса задач, как правило, не гарантируют правильность решения любых задач данного класса, и оптимальность решения рекомендуется проверять в каждом конкретном случае.

В экономических приложениях рассматриваются следующие классы задач НЛП.

1. Оптимизация нелинейной функции с ограничениями на неотрицательность значений переменных: F(х) ® mах,

x ³ 0,

где х = (х1, х2,..., хn) — вектор переменных задачи.

Пусть F(x) — дифференцируемая функция.

Необходимые условия того, что в точке х0 достигается максимум функции F(x):

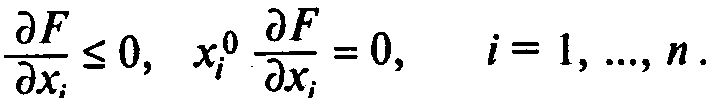
Это означает, что:

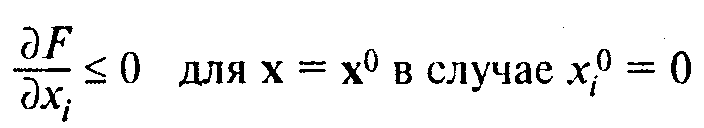
и

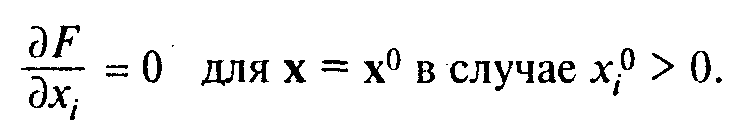
Если F(x) вогнутая функция (для задачи минимизации — выпуклая), то эти условия являются также достаточными.

Функция F(x) с числовыми значениями, определенная на выпуклом множестве точек К, называется вогнутой, если для любой пары точек х1, х2 и для всех чисел l, 0 £ l £ 1, выполняется неравенство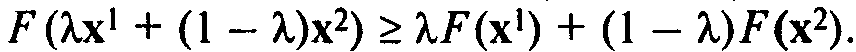

Если 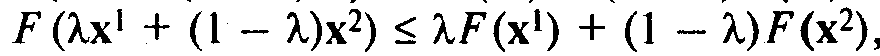то функция F(x) называется выпуклой. Если имеют место строгие неравенства, то говорят, что функция строго вогнута или строго выпукла.

Данное определение вогнутости (выпуклости) годится для любого типа функции. Практически, однако, применять его трудно.

Для дважды дифференцируемой функции F(x) имеет место следующий критерий. Дифференцируемая функция F(x) строго вогнута в некоторой окрестности точки 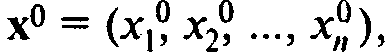если выполняются следующие условия:

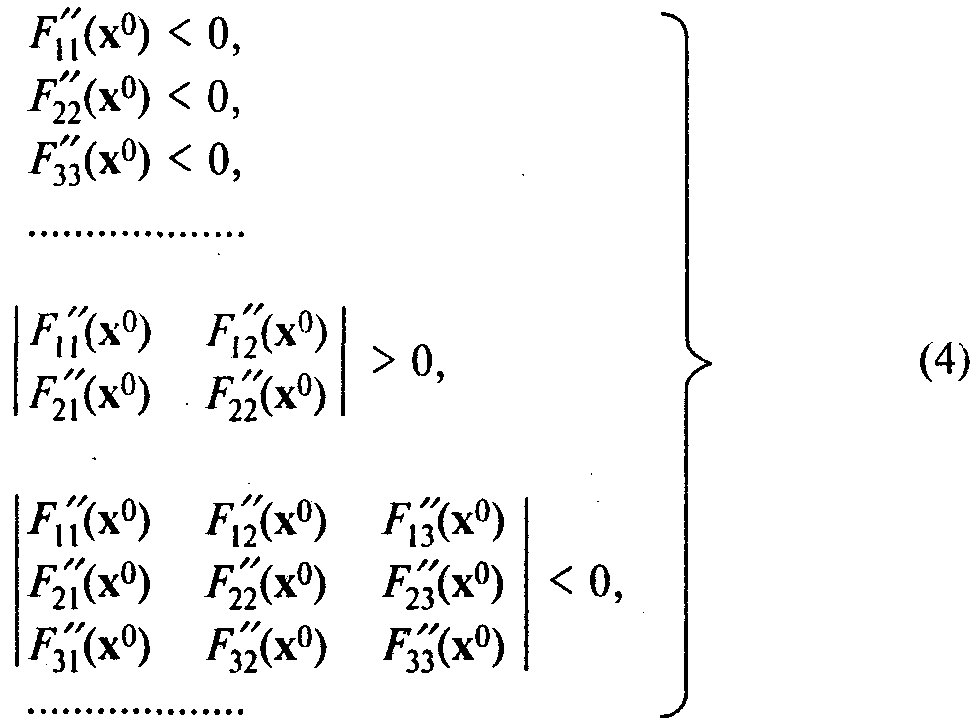
т.е. если знаки этих определителей чередуются указанным образом.

Здесь 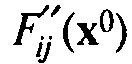— частная производная второго порядка, вычисленная в точке х0.

Матрица размера п ´ п, составленная из элементов 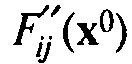, называется матрицей Хессе (Hesse). По значениям ее главных миноров можно судить о выпуклости или вогнутости функции. Функция F(x) строго выпукла в малой окрестности точки х0, если все главные миноры ее матрицы Хессе строго положительны. Если имеют место нестрогие неравенства (³), то функция в окрестности точки х0 выпукла. Если при этом главные миноры матрицы Хессе от х не зависят, то функция всюду (строго) выпукла.

Весьма распространены относящиеся к данному типу модели квадратичного программирования, в которых целевая функция F(x) является квадратичной функцией переменных х1, х2, ..., хn. Существует большое число алгоритмов решения такого типа задач, в которых функция F(x) вогнутая (для задач минимизации — выпуклая).

2. Модели выпуклого программирования. К такого рода моделям относятся задачи НЛП (1)—(3), в которых F(x) — вогнутая (выпуклая) функция, a gi(x) — выпуклые функции. При данных условиях локальный максимум (минимум) является и глобальным.

Пусть F(x) и gi(x), i= 1,..., т, — дифференцируемые функции.

Необходимые и достаточные условия оптимальности решения — выполнение условий Куна — Таккера.

Рассмотрим задачу НЛП (1)—(3) и функцию Лагранжа L (х, l) =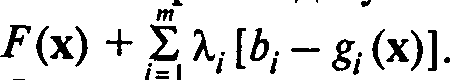

Условия Куна — Таккера оптимальности решения х0 для задачи максимизации F(x) имеют вид

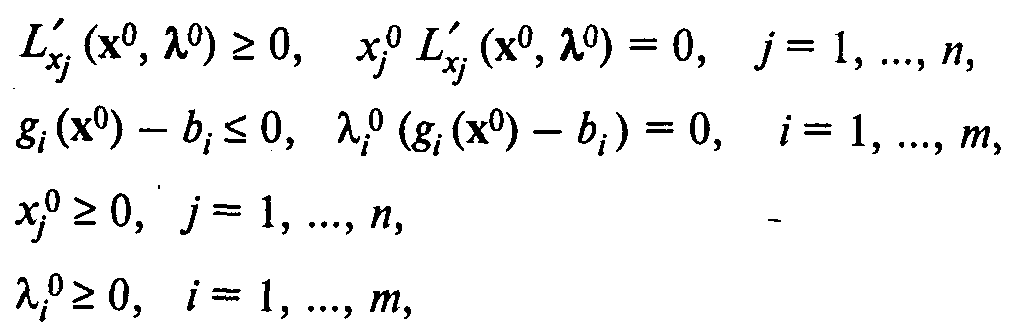
где 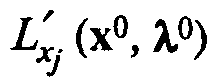— частная производная функции Лагранжа по переменной хj при х = х0 и l = l0. Пусть максимальное значение F(x) равно F(x0) = F0. Числа связаны с F0 следующими соотношениями: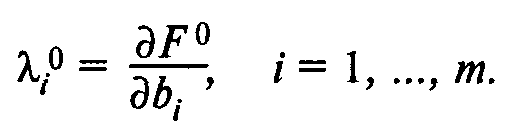

Из этих соотношений видно, что числа характеризуют реакцию значения F0 на изменение значения соответствующего bi. Например, если < 0, то при уменьшении bi (в пределах устойчивости ) значение F0 увеличится, а = 0 указывает на несущественность соответствующего ограничения gi(х) £ bi, которое может быть без ущерба для оптимального решения из системы ограничений исключено.

Примеры

Пример 1. Сколько производить?

Предприятие располагает ресурсами двух видов сырья и рабочей силы, необходимыми для производства двух видов продукции. Затраты ресурсов на изготовление одной тонны каждого продукта, прибыль, получаемая предприятием от реализации тонны продукта, а также запасы ресурсов указаны в следующей таблице:

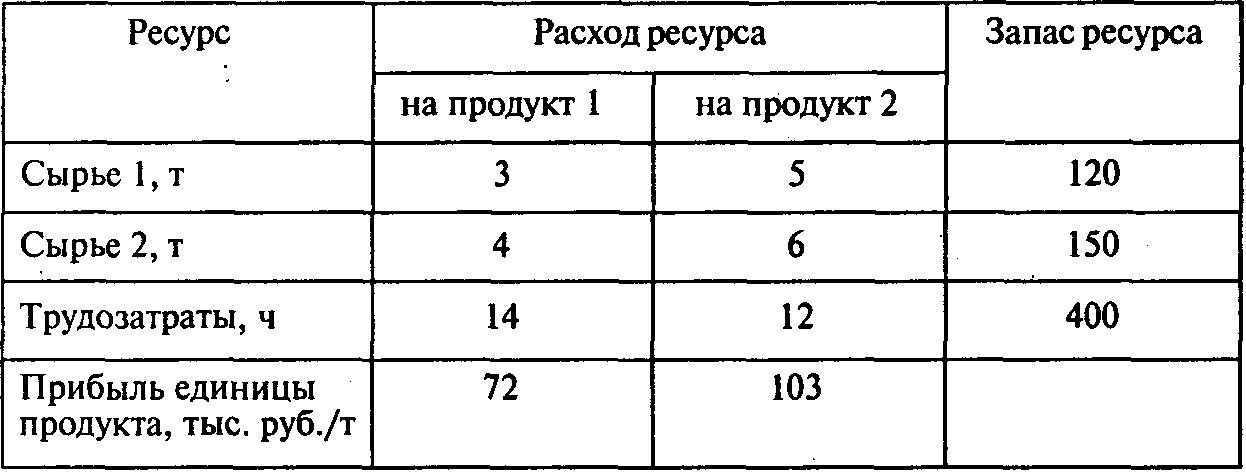
Стоимость одной тонны каждого вида сырья определяется следующими зависимостями: (9 + 0,0088r1) тыс. руб. для сырья 1 и (5 - 0,0086r2) тыс. руб. для сырья 2, где r1 и r2 — затраты сырья на производство продукции. Стоимость одного часа трудозатрат определяется зависимостью (1 - 0,0002r, где r — затраты времени на производство продукции.

Вопросы:

1. Сколько продукта 1 следует производить для того, чтобы обеспечить максимальную прибыль?

2. Сколько продукта 2 следует производить для того, чтобы обеспечить максимальную прибыль?

3. Какова максимальная прибыль?

Решение. Пусть x1 — объем выпуска продукта 1 (в тоннах), х2 — объем выпуска продукта 2 (в тоннах). Тогда задача может быть описана в виде следующей модели нелинейного программирования:

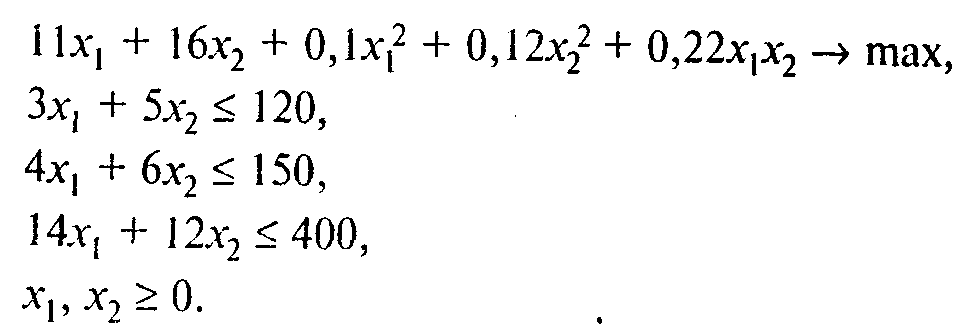
При использовании программы GINO исходную информацию для решения этой задачи представляем в следующем виде:

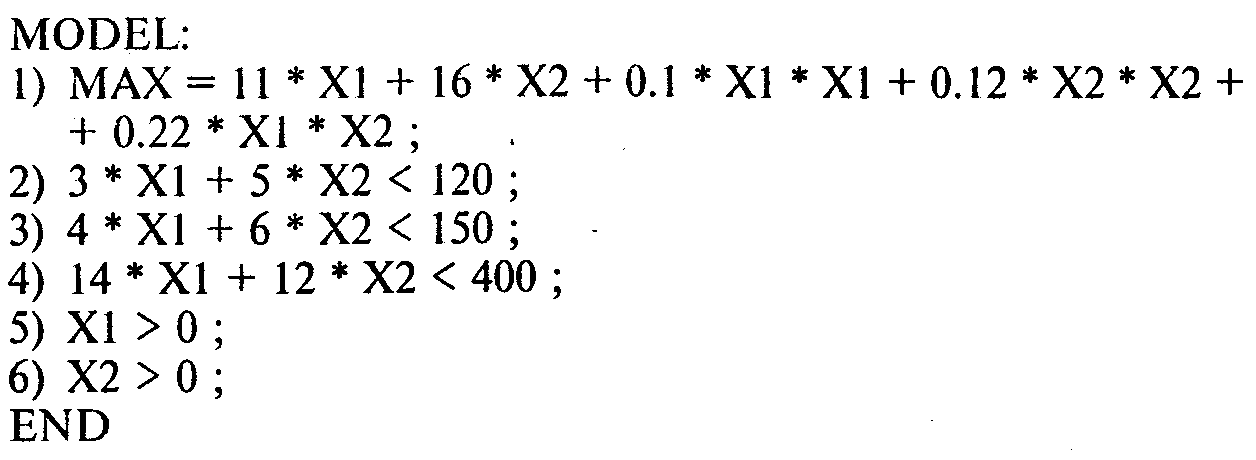
Получаем следующий результат:

Ответы: 1. 16,67т. 2.13,89т. 3. 507,407 тыс. руб.

Пример 2. Формирование портфеля ценных бумаг.

Клиент поручил брокерской конторе купить для него на 1 млн руб. акции трех известных ему компаний. Сделка заключается на год. Клиент заинтересован, с одной стороны, в максимизации средней прибыли на вложенный капитал, а с другой — в минимизации риска, поскольку прибыль, получаемая в конце года от ак­ции каждой компании, является величиной случайной. Известно, что чем прибыльнее акция, тем выше связанный с ней риск, поэтому названные критерии являются противоречивыми. Клиенту это обстоятельство разъяснили и попросили его указать относительную значимость («вес») критериев. Клиент, будучи человеком осторожным, высказал пожелание, чтобы риск учитывался с весом втрое большим, чем прибыль. Получив такие указания, сотрудники брокерской конторы сформулировали следующую модель нелинейного программирования:

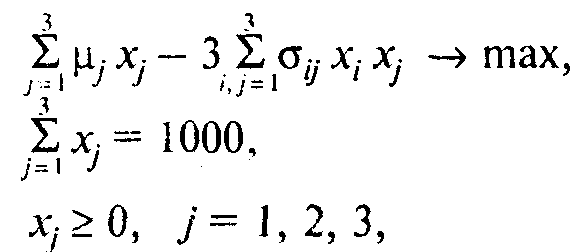
где хj — объем средств, затраченных на покупку акций типа j (тыс. руб.);

mj — математическое ожидание процента прибыли от вложения 1 тыс. руб. в акции типа j;

sjj — дисперсия указанного выше процента прибыли;

sij — ковариация между процентами прибыли от вложения 1 тыс. руб. в акции типа i и j (i ¹ j).

Первая сумма в критерии — ожидаемое значение прибыли, обеспечиваемой пакетом акций, вторая — дисперсия прибыли пакета акций, взятая с «весом» 3. Дисперсия прибыли пакета акций служит мерой риска. Пусть средние значения процентов годовой прибыли от акций компаний составляют соответственно 8, 10 и 13%. Дисперсии s11 = 0,1, s22 = 0,15, s33 = 0.19. Ковариации s12 = 0,01, s13 = 0,02, s23 = 0,03.

Вопросы:

1. Является ли целевая функция строго вогнутой?

2. Какую сумму следует вложить в покупку акций типа 1?

3. Какую сумму следует вложить в покупку акций типа 3?

Решение. Модель нелинейного (в данном случае — квадратичного) программирования имеет вид

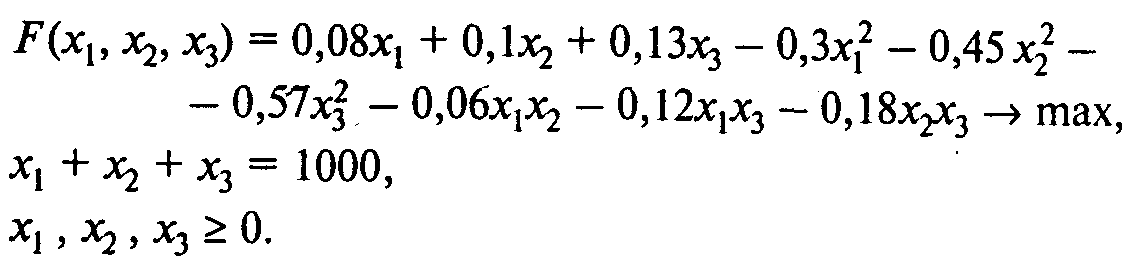
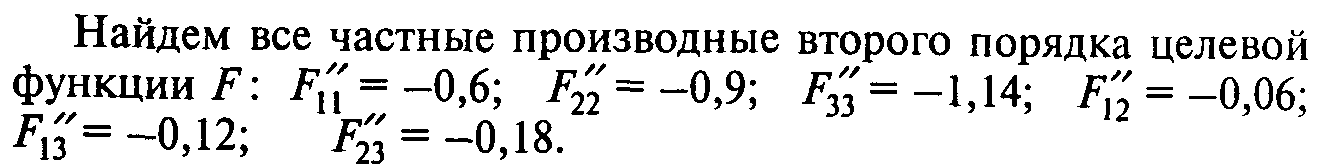
Рассчитав значения соответствующих определителей (главных миноров матрицы Хессе), можно убедиться, что выполняются условия (4), откуда следует, что целевая функция строго выпукла для любых значений х1, х2, х3 (значения определителей не зависят от значений переменных).

Используя программу GINO, исходную информацию для решения этой задачи представляем в следующем виде:

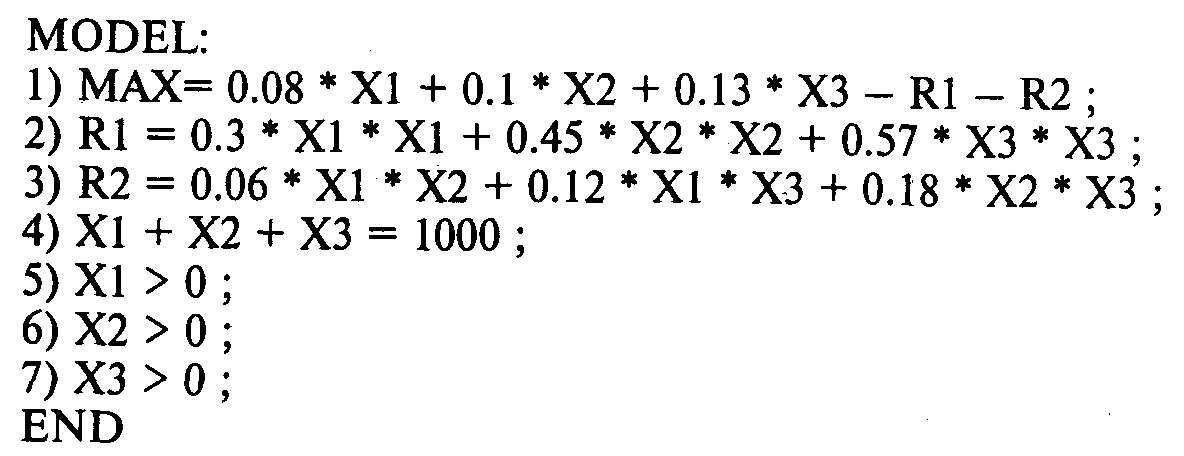
Получаем следующий результат:

Непосредственной подстановкой полученного решения в условия (5)—(8) можно убедиться, что условия Куна — Таккера выполняются, причем решение обеспечивает глобальный максимум целевой функции, поскольку F строго вогнута.

Ответы: 1. Да, является (при любых значениях переменных).

2. 496,8 тыс. руб. 3. 197,93 тыс. руб.