Транспортная задача с ограничениями на пропускную способность

Пусть требуется при решении транспортной задачи ограничить перевозки от поставщика с номером l к потребителю с номером k. Возможны ограничения двух типов: 1) ; 2) , где a и b – постоянные величины.

1. Если , то необходимо прежде, чем решать задачу, сократить (уменьшить) запасы l-го поставщика и запросы k-го потребителя на величину a (зарезервировать перевозку ). После решения задачи в оптимальном решении следует увеличить объем перевозки на величину a.

2. Если , то необходимо вместо k-го потребителя с запросами ввести двух других потребителей. Один из них с номером k должен иметь запросы , а другой с номером n + 1 – запросы . Стоимости перевозок для этих потребителей остаются прежними, за исключением стоимости , которая принимается равной сколь угодно большому числу М (M >> 1). После получения оптимального решения величины грузов, перевозимых к (n + 1)-му потребителю, прибавляются к величинам перевозок k-го потребителя. Так как - самая большая стоимость перевозки, то в оптимальном решении клетка с номером (l, n+1) остается пустой и объем перевозки не превзойдет b.

Пример 6.6. Решить транспортную задачу, исходные данные которой приведены в табл. 6.20 при дополнительных условиях: объем перевозки груза от 1-го поставщика 2-му потребителю должен быть не менее 100 единиц ( ), а от 3-го 1-му не более 200 единиц ( ).

Т а б л и ц а 6.20

Решение. Для того чтобы в оптимальном решении объем перевозки был не менее 100 единиц, при решении задачи будем предполагать, что запасы 1-го поставщика и запросы 2-го потребителя меньше фактических на 100 единиц. После получения оптимального решения объем перевозки увеличим на 100 единиц.

Для того чтобы удовлетворить требованию , вместо 1-го потребителя введем двух других. Один из них под прежним первым номером имеет запросы = 200 единиц и прежние стоимости перевозок единиц груза. Другому присвоим 4-й номер. Его запросы равны = 500 -200 = 300 единиц и стоимости перевозок единиц груза те же, что и у 1-го потребителя, за исключением , которую примем равной сколь угодно большому числу М, т. е. = М. После нахождения оптимального решения задачи объемы перевозок для 4-го потребителя необходимо прибавить к соответствующим объемам перевозок для 1-го потребителя.

В результате указанных преобразований таблица исходных данных задачи будет иметь следующий вид (табл. 6.21).

Т а б л и ц а 6.21

				М

Далее задачу решаем обычным методом потенциалов. Проверяем выполнение необходимого и достаточного условий существования решения задачи. Находим суммарные запасы поставщиков и запросы потребителей.

= 100 + 300 + 500 = 900;

= 200+300+300+300 = 1100.

Задача с неправильным балансом. Вводим фиктивного поставщика с запасами = 1100 - 900 = 200 (табл. 6.22).

Составляем начальное опорное решение методом минимальной стоимости. Записываем матрицу стоимостей С. Кружочками в матрице С отмечены минимальные элементы, а цифрами рядом со строками и столбцами - порядок исключения из рассмотрения поставщиков и потребителей.

Т а б л и ц а 6.22

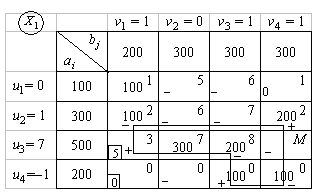
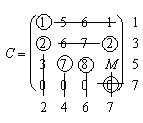
Полученное решение имеет m + n - 1 = 4 + 4 -1 = 7 базисных переменных. Вычислим значение целевой функции на этом опорном решении

= 100 × 1 + 100 × 2 + 200 × 2 + 300 × 7 + 200 × 8 + 100 × 0 + 100 × 0 = 4400.

Для проверки оптимальности опорного решения находим потенциалы. Записываем систему уравнений для нахождения потенциалов и решаем ее:

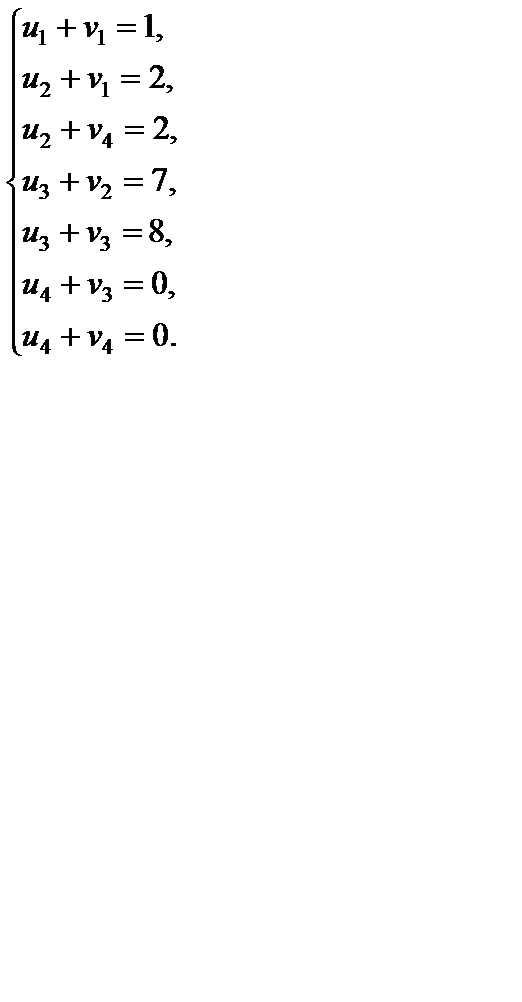
Система состоит из семи уравнений и имеет восемь переменных. Так как число неизвестных на единицу больше числа уравнений, то одному из потенциалов можно задать значение произвольно: пусть = 0. Остальные потенциалы однозначно находятся из системы уравнений

= 1 – 0 = 1;

= 2 – 1 = 1;

= 2 – 1 = 1;

= 0 – 1 = –-1;

= 0 – (–1) = 1;

= 8 – 1 = 7;

= 7 – 7 = 0.

Значения потенциалов приведены в табл. 6.22. Находим оценки для свободных клеток таблицы:

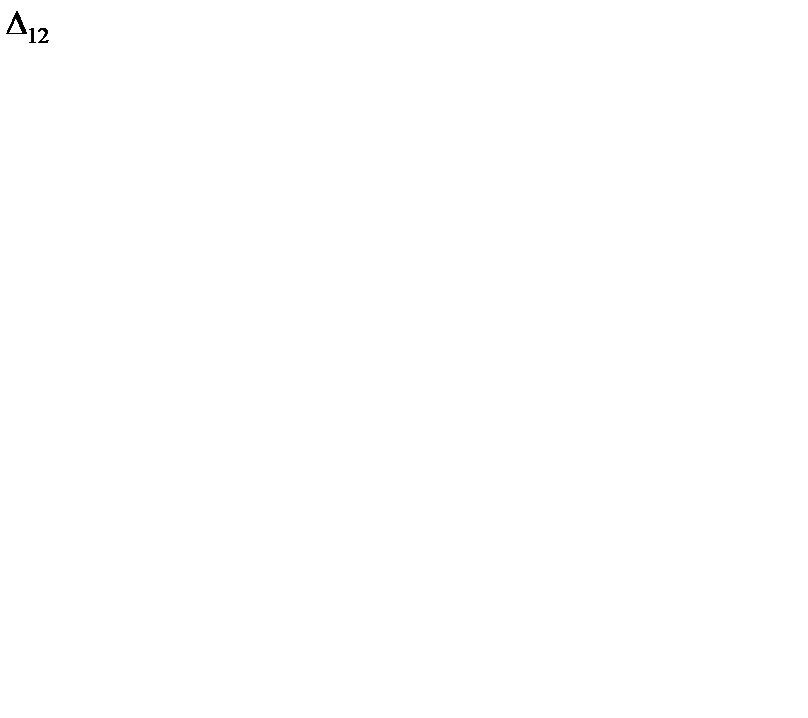= 0 + 0 - 5 = -5 < 0;

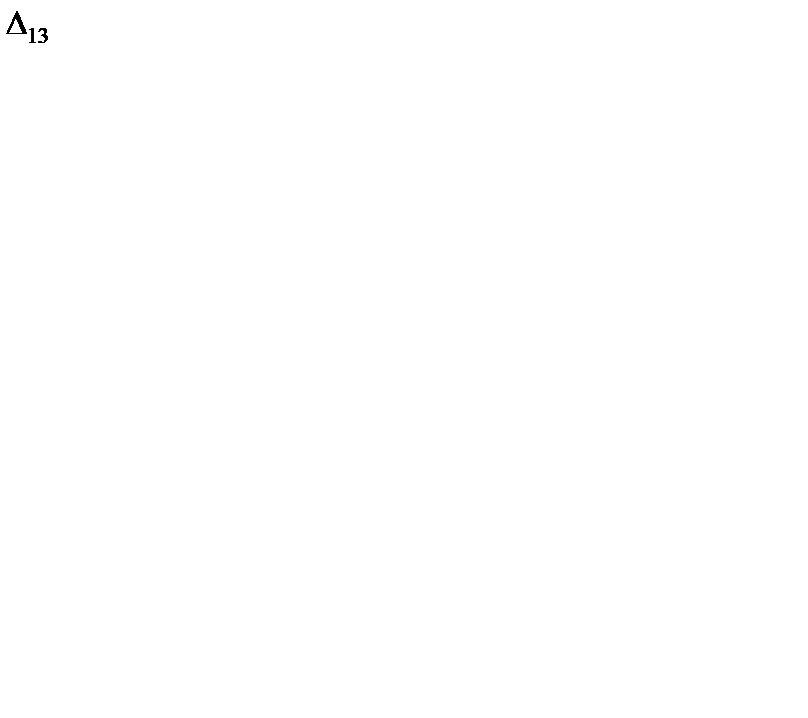= 0 + 1 - 6 = - 5 < 0;

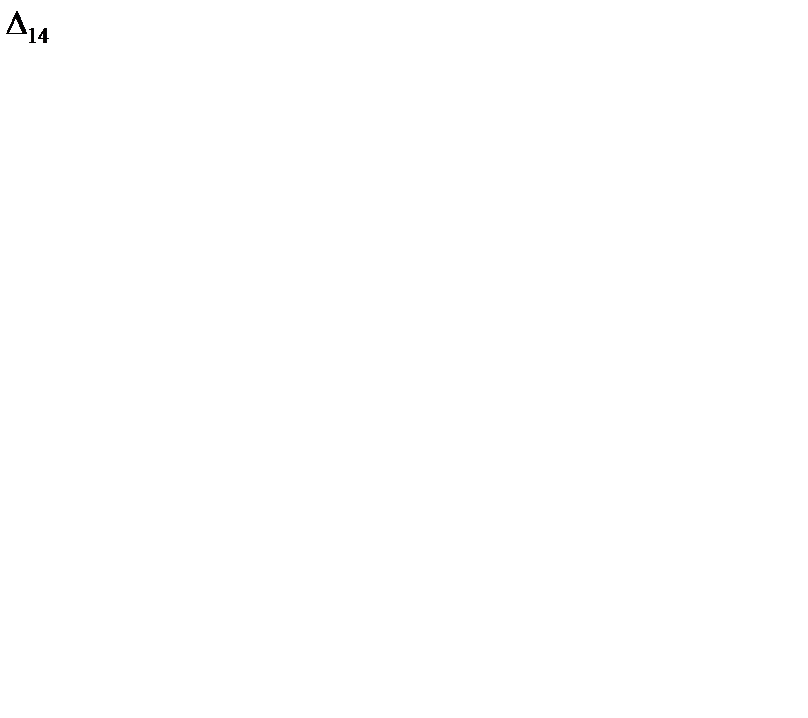= 0 + 1 - 1 = 0;

= 1 + 0 - 6 = -5 < 0;

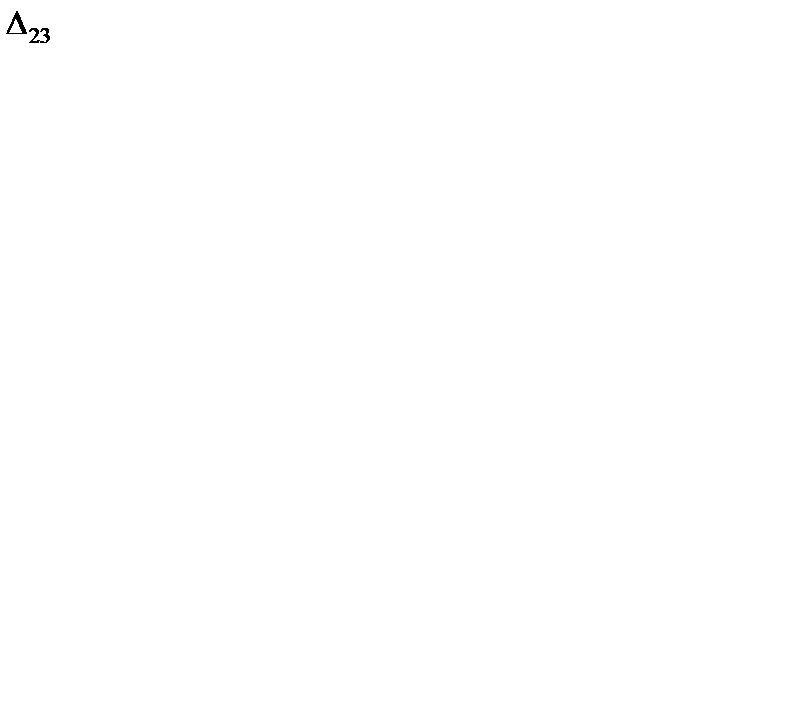= 1 + 1 - 7 = - 5 < 0;

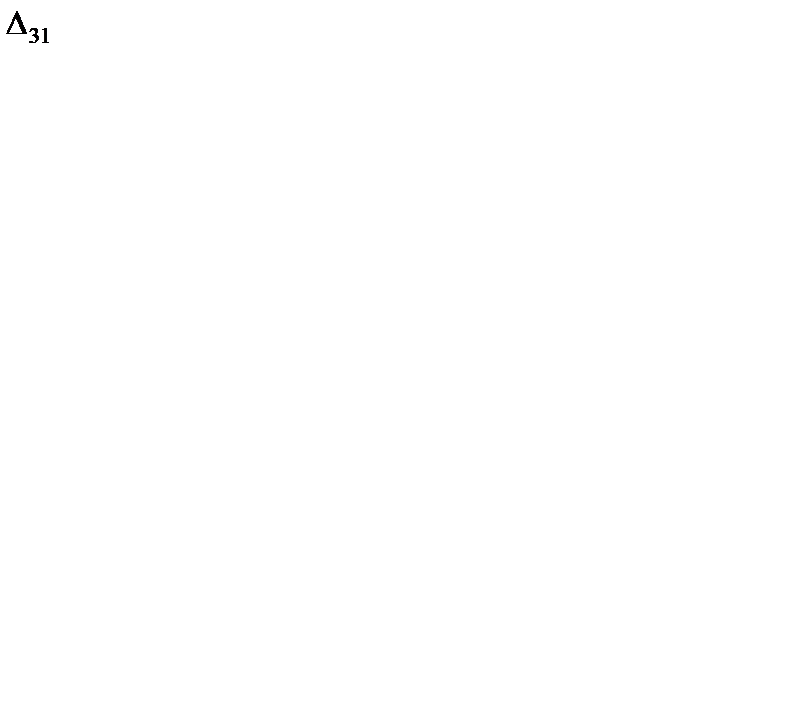= 7 + 1 - 3 = 5 > 0;

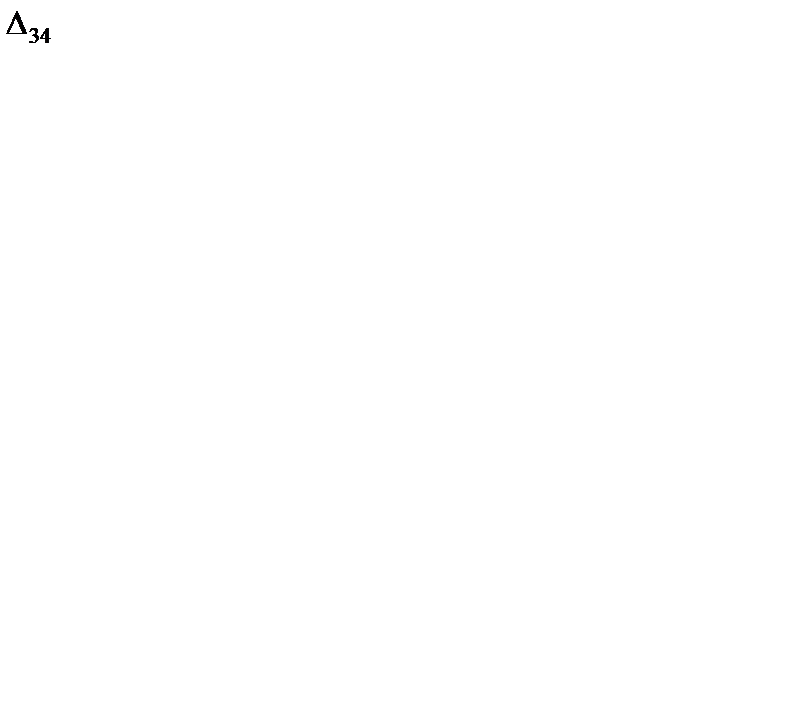= 7 + 1 - M = < 0;

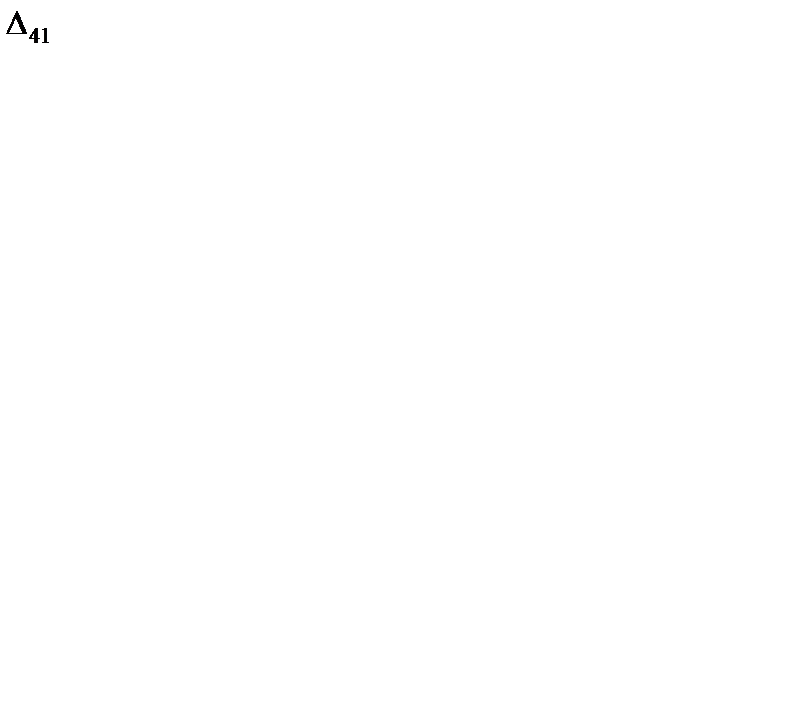= -1 + 1 - 0 = 0;

= -1 + 0 - 0 = -1 < 0.

Опорное решение неоптимальное, так как имеется положительная оценка 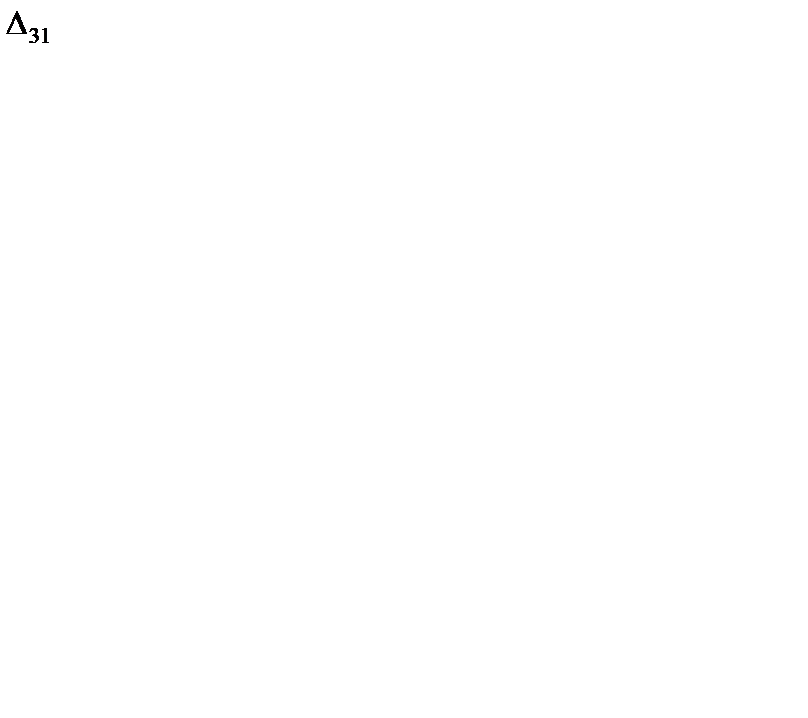= 5 для клетки (3, 1). Отмечаем эту клетку знаком "+". Находим цикл для улучшения опорного решения (табл. 6.22). Определяем величину груза для перераспределения по циклу {100, 200, 100} = 100. Осуществляем сдвиг по циклу на величину q = 100. Получаем второе опорное решение 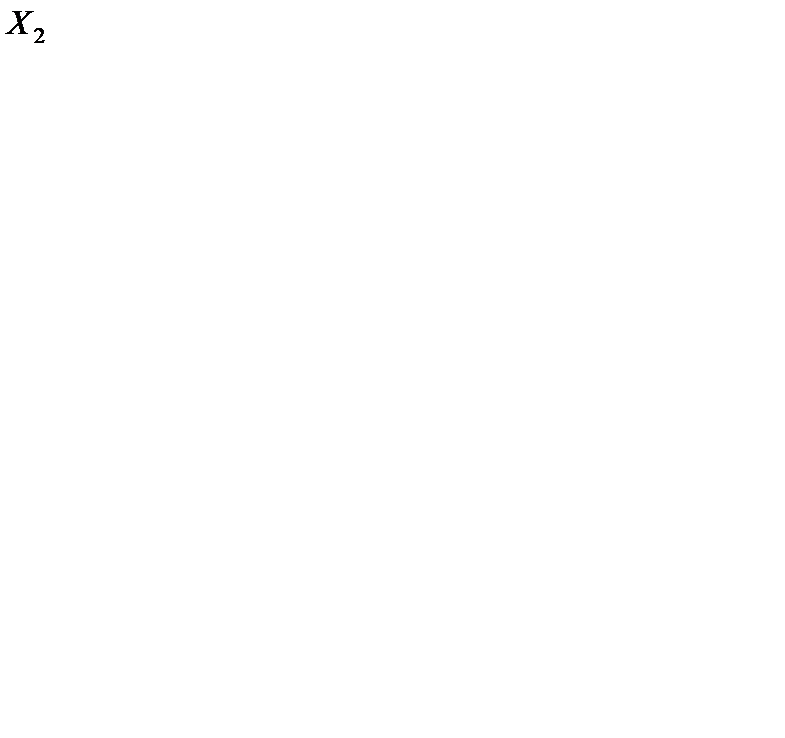(табл. 6.23).

Т а б л и ц а 6.23

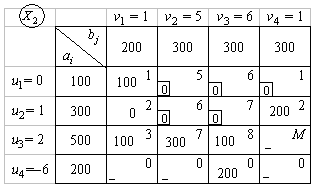
В табл. 6.23 также записаны потенциалы и оценки для свободных клеток. Решение 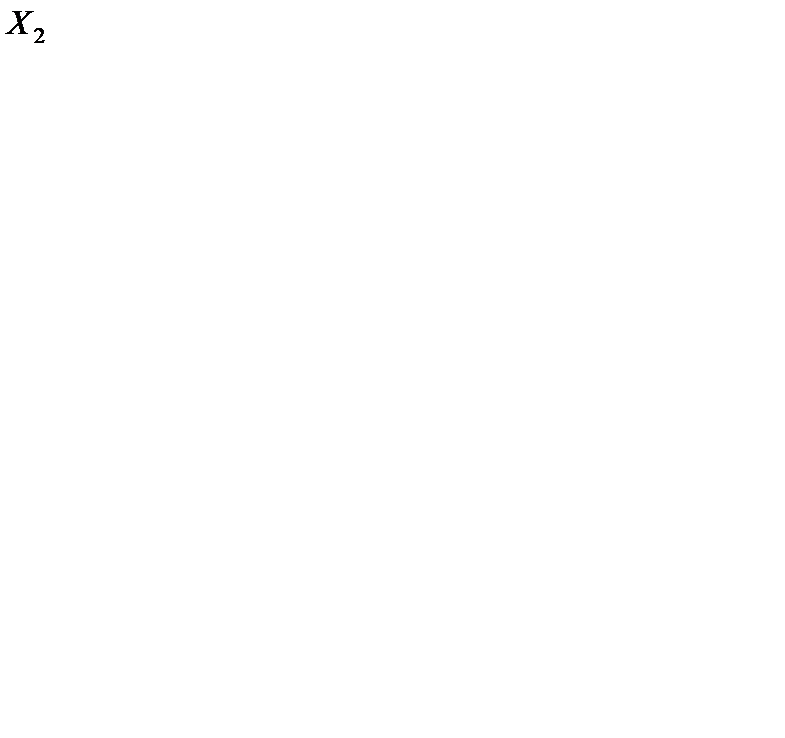оптимальное, так как все оценки неположительные. Запишем оптимальное решение исходной задачи. Для этого увеличим объем перевозки на 100 единиц и объединим объемы перевозок 4-го потребителя с объемами перевозок 1-го потребителя. Получим

.

Вычислим значение целевой функции на этом решении

= 100 × 1 + 100 × 5 + 300 × 2 + 100 × 3 + 300 × 7 + 100 × 8 = 4400.

Ответ: min Z(X) = 4400 при .

В некоторых задачах требуется запретить перевозки от отдельных поставщиков отдельным потребителям. В таких случаях либо зачеркивают клетку таблицы транспортной задачи, либо назначают соответствующую этой клетке стоимость перевозки единицы груза сколь угодно большой, равной M >> 1. В остальном задача решается обычным способом. Для разрешимости данной задачи необходимо существование начального опорного решения.