РАСЧЕТ И АНАЛИЗ СЕТЕВЫХ МОДЕЛЕЙ
Календарное планирование предусматривает определение моментов начала и окончания каждой работы и других временных характеристик сетевого графика. Это позволяет проанализировать сетевую модель, выявить критические работы, непосредственно определяющие срок выполнения проекта, провести оптимизацию использования ресурсов (временных, финансовых, исполнителей).
Расчет сетевой модели начинают с временных параметров событий, которые вписывают непосредственно в вершины сетевого графика (рис.8.1):
· 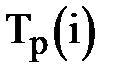 – ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i;
– ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i;
· 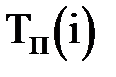 – поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети;
– поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети;
· 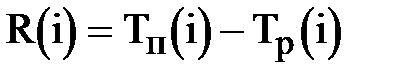 – резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения проекта в целом.
– резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения проекта в целом.

Рис.8.1. Отображение временных параметров событий на сетевом графике
Ранние сроки свершения событий 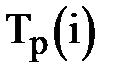 рассчитываются от исходного (И) к завершающему (З) событию следующим образом:
рассчитываются от исходного (И) к завершающему (З) событию следующим образом:
1) для исходного события И 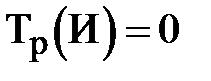 ;
;
2) для всех остальных событий I
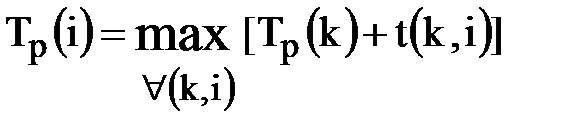 ,
,
где максимум берется по всем работам 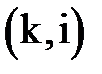 , входящим в событие i;
, входящим в событие i; 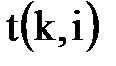 – длительность работы (k,i) (рис.8.2).
– длительность работы (k,i) (рис.8.2).

Рис.8.2. Расчет раннего срока 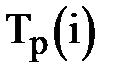 свершения события i
свершения события i
Поздние сроки свершения событий 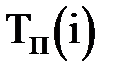 рассчитываются от завершающего к исходному событию:
рассчитываются от завершающего к исходному событию:
1) для завершающего события З 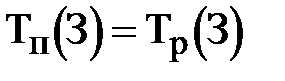 ;
;
2) для всех остальных событий
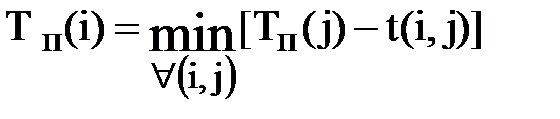 ,
,
где минимум берется по всем работам 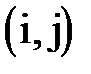 , выходящим из события i;
, выходящим из события i; 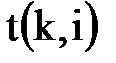 – длительность работы (k,i) (рис.8.3).
– длительность работы (k,i) (рис.8.3).

Рис.8.3. Расчет позднего срока 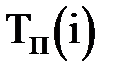 свершения события i
свершения события i
Временные параметры работ определяются на основе ранних и поздних сроков событий:
· 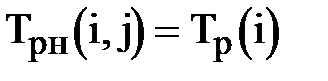 – ранний срок начала работы;
– ранний срок начала работы;
· 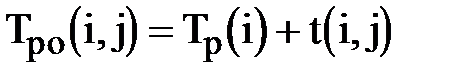 – ранний срок окончания работы;
– ранний срок окончания работы;
· 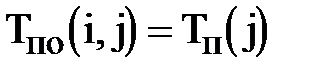 – поздний срок окончания работы;
– поздний срок окончания работы;
· 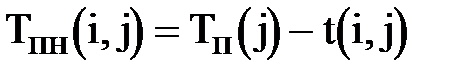 – поздний срок начала работы;
– поздний срок начала работы;
· 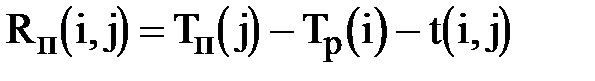 – полный резерв работы показывает максимальное время, на которое можно увеличить длительность работы
– полный резерв работы показывает максимальное время, на которое можно увеличить длительность работы 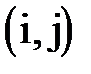 или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом;
или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом;
· 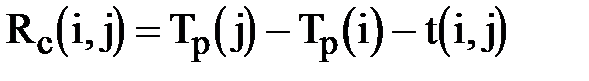 – свободный резерв работы показывает максимальное время, на которое можно увеличить продолжительность работы
– свободный резерв работы показывает максимальное время, на которое можно увеличить продолжительность работы 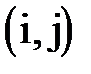 или отсрочить ее начало, не меняя ранних сроков начала последующих работ.
или отсрочить ее начало, не меняя ранних сроков начала последующих работ.
Путь – это последовательность работ в сетевом графике (в частном случае это одна работа), в которой конечное событие одной работы совпадает с начальным событием следующей за ней работы. Полный путь – это путь от исходного до завершающего события. Критический путь – максимальный по продолжительности полный путь. Работы, лежащие на критическом пути, называют критическими.Критические работы имеют нулевые свободные и полные резервы. Подкритический путь – полный путь, ближайший по длительности к критическому пути.
Для проведения анализа временных параметров сетевой модели используют график привязки, который отображает взаимосвязь выполняемых работ во времени. По вертикальной оси графика привязки откладываются коды работ, по горизонтальной оси – отрезки, соответствующие длительностям работ (раннее начало и раннее окончание работ). График привязки можно построить на основе данных о продолжительности работ. При этом необходимо помнить, что работа 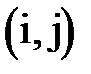 может выполняться только после того как будут выполнены все предшествующие ей работы
может выполняться только после того как будут выполнены все предшествующие ей работы 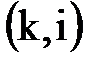 .
.
Лекция №15 Динамическое программирование
Суть методов динамического программирования
В задачах динамического программирования экономический процесс зависит от времени (или от нескольких периодов времени), поэтому находится ряд оптимальных решений (последовательно для каждого этапа), обеспечивающих оптимальное развитие всего процесса в целом. Динамическое программирование представляет собой математический аппарат, позволяющий осуществлять оптимальное планирование управляемых процессов и процессов, зависящих от времени. Поэтапное проведение оптимизации называется многошаговым процессом принятия решения. Экономический процесс называется управляемым, если можно влиять на ход его развития.
В основе метода динамического программирования (ДП) лежит принцип последовательной оптимизации: решение исходной задачи оптимизации большой размерности заменяется решением последовательности задач оптимизации малой размерности. Основным условием применимости метода ДП является возможность разбиения процесса принятия решений на ряд однотипных шагов или этапов, каждый из которых планируется отдельно, но с учетом результатов, полученных на других шагах. Например, деятельность отрасли промышленности в течение ряда хозяйственных лет или же последовательность тестов, применяемых при контроле аппаратуры, и т. д. Некоторые процессы (операции) расчленяются на шаги естественно, но существуют такие операции, которые приходится делить на этапы искусственно, например процесс наведения ракеты на цель.
Этот принцип гарантирует, что управление, выбранное на любом шаге, является не локально лучшим, а лучшим с точки зрения процесса в целом, так как это управление выбирается с учетом последствий на предстоящих шагах. Динамическое программирование.
Задача распределения ресурсов.
Динамическое программирование – это математический метод нахождения оптимальных решений многошаговых (многоэтапных) задач. Динамическое программирование дает возможность принять ряд последовательных решений, обеспечивающих оптимальность развития процесса в целом.
1. Постановка задачи динамического программирования. Функция Беллмана.
В начальный момент времени система находится в состоянии S0.
На 1-м шаге под действием переменной управления x1 система переходит из состояния S0 в состояние S1, то есть S1=S1(S0,x1). Здесь целевая функция равна F1(S0,x1).
На 2-м шаге под действием переменной управления х2 система переходит из состояния S1 в состояние S2, то есть S2=S2(S1,x2). Здесь целевая функция равна F2(S1,x2).
На 3-м шаге под действием переменной управления x3 система переходит из состояния S2 в состояние S3, то есть S3=S3(S2,x3). Здесь целевая функция равна F3(S2,x3). И т. д.
На последнем n-м шаге под действием переменной управления хп система переходит из состояния Sn–1 в состояние Sn, то есть Sn=Sn(Sn-1,xn).
Здесь целевая функция равна Fn(Sn-1,xn).
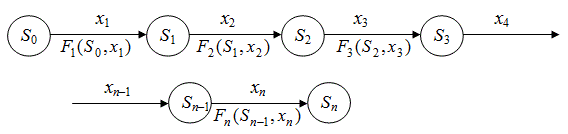
Обозначим через X=(x1,x2,...,xn) управление, переводящее систему за n шагов из начального состояния S0 в конечное состояние Sn.
Целевая функция на k-м шаге X=(x1,x2,...,xn) управление, переводящее систему за n шагов из начального состояния S0 в конечное состояние Sn.
Целевая функция на k-м шаге Fk(Sk-1,xk) (k=1,2,...n) называется функцией Беллмана.
Наша задача – так подобрать управление X, переводящее систему за n шагов из начального состояния S0 в конечное состояние Sn, чтобы достичь экстремума (максимума или минимума в зависимости от вида решаемой задачи) целевой функции 
2. Принцип оптимальности Беллмана
В основе решения задач динамического программирования лежит принцип оптимальности Беллмана: на каждом этапе принимается такое решение, которое обеспечивает оптимальность с данного этапа до конца процесса, то есть на каждом этапе необходимо принимать решение, просматривая его последствия до самого конца процесса. Так как последовательность решений следует просматривать до самого конца процесса, то варианты анализируют с конца процесса.
3. Функциональные уравнения Беллмана
Функциональные уравнения Беллмана – это математическая формулировка принципа оптимальности Беллмана. Оптимальное управление обладает следующим свойством: каковы бы ни были начальное состояние S0 и решение в начальный момент времени, последующие решения должны составлять оптимальное управление относительно состояния, полученного в результате предыдущего решения.
Будем считать, что мы ищем максимум целевой функции. На n-м шаге, то есть «выигрыш» на n-м шаге зависит только от выбора управления хn на этом шаге.
На (n–1)-м шаге
то есть на (n–1)-м шаге надо так подобрать управление хn–1, чтобы сумма выигрышей на (n–1)-м шаге Fn-1(Sn-2,xn-1) и на n-м шаге Zn(Zn-1(Sn-2,xn-1)) была максимальна.
На (n–2)-м шаге 
то есть на (n–2)-м шаге надо так подобрать управление хn–2, чтобы сумма выигрышей на (n–2)-м шаге Fn-2 (Sn-3,xn-2) и на двух последних шагах Zn-1 (Zn-1(Sn-3,xn-2)) была максимальна. И т. д.
На k-м шаге 
(k = n–1, n–2, ...., 2, 1), то есть на k-м шаге надо так подобрать управление хk, чтобы сумма выигрышей на k-м шаге F=(Sk-1,xk) и на n–k последующих шагах Zk+1(Sk(Sk-1,xk)) была максимальна.
4. Общая схема решения задачи динамического программирования
Определяем все состояния системы при переходе из начального состояния S0 в конечное состояние Sn, вид целевых функций на каждом шаге Fk (Sk-1,xk) (k=1,2,....n), функции перехода Sk(Sk-1,xk) из состояния Sk–1 в состояние Sk. Запишем уравнения Беллмана.
Из уравнения Беллмана для Z1(S0) по S0 находим оптимальное управление на 1-м шаге x1*. По S0 и x1*определяем состояние системы после 1-го шага: S1=S1(S0,x1).
Из уравнения Беллмана для Z2(S1) по S1 находим оптимальное управление на 2-м шаге x2*. По S1 и x2* определяем состояние системы после 2-го шага: S2=S2(S1,x2) .
Из уравнения Беллмана для Z3(S2) по S2 находим оптимальное управление на 3-м шаге x3* . И т. д.
S0 → x1* → S1 → x2* →S2 → x3* → ... → Sn-1 → xn*
5. Задача распределения ресурсов
Между четырьмя предприятиями распределяются 60 млн. руб. Прирост выпуска продукции на каждом предприятии зависит от выделенной суммы средств х. Значения прироста задаются в виде таблицы gi(x), i = 1, 2, 3, 4. Найти такой план распределения 60 млн. руб. между предприятиями, при котором общий прирост выпуска продукции будет максимальным.
| Средства x , млн. руб. | Прирост выпуска продукции, млн. руб. | |||
| g1(x) | g2(x) | g3(x) | g4(x) | |
Начальное состояние S0= 60 млн. руб. Разобьем весь процесс выделения средств предприятиям на 4 шага.
На 1-м шаге выделим x1 млн. руб. 1-му предприятию. После этого останется S1 = S0 – x1 млн. руб.
На 2-м шаге выделим x2 млн. руб. 2-му предприятию. После этого останется S2 = S1 – x2 млн. руб.
На 3-м шаге выделим x3 млн. руб. 3-му предприятию. После этого останется S3 = S2 – x3 млн. руб.
На 4-м шаге выделим x4 млн. руб. 4-му предприятию.
Уравнения Беллмана  то есть на k-м шаге из оставшихся Sk–1 средств надо выделить xk средств
то есть на k-м шаге из оставшихся Sk–1 средств надо выделить xk средств
k-му предприятию, чтобы прирост выпуска продукции на k-м и оставшихся предприятиях был максимальным.
Пусть k = 4. Тогда 
В столбце S3 и строке х4 указаны все возможные значения. Все оставшиеся перед 4-м шагом средства нужно выделить 4-му предприятию. Поэтому числа из столбца g4(x) исходной таблицы запишем в нашу таблицу в столбцы со 2-го по 5-й. В столбцах со 2-го по 5-й определяем максимум в каждой строке, и результат пишем в 6-й столбец. Те x4, которым соответствуют числа из 6-го столбца, пишем в 7-й столбец.
| x4 S3 | Z4(S3) | x4* | ||||
Пусть k = 3. Тогда

Определим оптимальную стратегию при распределении средств между 3-м и 4-м предприятиями. По первоначальной таблице и таблице при k = 4 заполним следующую таблицу.
В 1-м столбце указано, сколько средств осталось для 3-го и 4-го предприятий. В строке х3 дана информация о том, сколько из этих оставшихся средств досталось 3-му предприятию. Поясним, как заполняются столбцы со 2-го по 5-й. В клетке (2, 2) (2-я строка, 2-й столбец) на долю 3-го и 4-го предприятий приходится S2 = 0, из них на долю 3-го предприятия приходится х3 = 0. Поэтому нужно сложить значения из исходной таблицы для g3(x) при х=0 (это 0) и из предпоследнего столбца предыдущей таблицы при S3 = S2 – х3 = 0 – 0 = 0 (это 0), то есть 0 + 0 = 0.
В клетке (3, 2) (3-я строка, 2-й столбец) на долю 3-го и 4-го предприятий приходится S2 = 20, из них на долю 3-го предприятия приходится х3 = 0. Поэтому нужно сложить значения из исходной таблицы для g3(x) при х = 0 (это 0) и из предпоследнего столбца предыдущей таблицы при S3 = S2 – х3 = 20 – 0 = 20 (это 14), то есть 0 + 14 = 14.
В клетке (5, 3) (5-я строка, 3-й столбец) на долю 3-го и 4-го предприятий приходится S2 = 60, из них на долю 3-го предприятия приходится х3 = 20. Поэтому нужно сложить значения из исходной таблицы для g3(x) при х = 20 (это 14) и из предпоследнего столбца предыдущей таблицы при S3 = S2 – х3 = 60 – 20 = 40 (это 20), то есть
14 + 20 = 34. И т. д.
| x3 S2 | Z3(S2) | x3* | |||||
| 0+0=0 | |||||||
| 0+14=14 | 14+0=14 | 0или 20 | |||||
| 0+20=20 | 14+14=28 | 21+0=21 | |||||
| 0+35=35 | 14+20=34 | 21+14=35 | 34+0=34 | 0 или 40 |
В столбцах со 2-го по 5-й определяем максимум в каждой строке, и результат пишем в 6-й столбец. Те х3, которым соответствуют числа из 6-го столбца, пишем в 7-й столбец. Пусть k = 2.
Определим оптимальную стратегию при распределении средств между 2-м, 3-м и 4-м предприятиями. По первоначальной таблице и таблице при k = 3 заполним следующую таблицу.
| 2 S1 | Z2(S1) | x2* | |||||
| 0+0=0 | |||||||
| 0+14=14 | 6+0=6 | ||||||
| 0+28=28 | 6+14=20 | 23+0=23 | |||||
| 0+35=35 | 6+28=34 | 23+14=37 | 30+0=30 |
В 1-м столбце указано, сколько средств осталось для 2-го, 3-го и 4-го предприятий. В строке х2 дана информация о том, сколько из этих оставшихся средств досталось 2-му предприятию. Поясним, как заполняются столбцы со 2-го по 5-й.
Например, в клетке (5, 4) (5-я строка, 4-й столбец) на долю 2-го, 3-го и 4-го предприятий приходится S1 = 60, из них на долю 2-го предприятия приходится х2 = 40. Поэтому нужно сложить значения из исходной таблицы для g2(x) при х = 40 (это 23) и из предпоследнего столбца предыдущей таблицы при S2 = S1 – х2 = 60 – 40 = 20 (это 14), то есть
23 + 14 = 37. И т. д.
В столбцах со 2-го по 5-й определяем максимум в каждой строке, и результат пишем в 6-й столбец. Те х2, которым соответствуют числа из
6-го столбца, пишем в 7-й столбец.
Пусть k = 1. Тогда
Определим оптимальную стратегию при распределении средств между предприятиями. По первоначальной таблице и таблице при k = 2 заполним следующую таблицу.
| x1 S0 | Z1(S0) | x1* | |||||
| 0+0=0 | |||||||
| 0+14=14 | 7+0=7 | ||||||
| 0+28=28 | 7+14=21 | 23+0=23 | |||||
| 0+37=37 | 7+28=35 | 23+14=37 | 31+0=31 | 0 или 40 |
В 1-м столбце указано общее количество средств. В строке x1 дана информация о том, сколько из этих средств досталось 1-му предприятию. Поясним, как заполняются столбцы со 2-го по 5-й.
Например, в клетке (4, 3) (4-я строка, 3-й столбец) на долю предприятий приходится S0 = 40, из них на долю 1-го предприятия приходится x1 = 20. Поэтому нужно сложить значения из исходной таблицы для g1(x) при х = 20 (это 7) и из предпоследнего столбца предыдущей таблицы при S1 = S0 – x1 = 40 – 20 = 20 (это 14), то есть
7 + 14 = 21. И т. д.
В столбцах со 2-го по 5-й определяем максимум в каждой строке и результат пишем в 6-й столбец. Те x1, которым соответствуют числа из
6-го столбца, пишем в 7-й столбец.
Максимальное значение Z1(S0) (в 6-м столбце) равно 37 при S0 = 60 и x1* = 0 или 40. Если x1*= 0, то S1 = S0 –x1* = 60 – 0 = 60.
Из таблицы при k = 2 и S1 = 60 находим в последнем столбце x2*= 40. Тогда S2 = S1 –x2* = 60 – 40 = 20.
Из таблицы при k = 3 и S2 = 20 находим в последнем столбце x3*= 0 или 20. Если x3*= 0, то S3 = S2 –x3* = 20 – 0 = 20.
Из таблицы при k = 4 и S3 = 20 находим в последнем столбце x4*= 20.
Получен один оптимальный вариант распределения средств: x1*= 0, x2*= 40, x3*= 0, x4*= 20.
Если x3*= 20, то S3 = S2 –x3* = 20 – 20 = 0. Из таблицы при k = 4 и S3=0 находим в последнем столбце x4*= 0.
Получен еще один оптимальный вариант распределения средств: x1*=0, x2*=40, x3*=20, x4*=0.
Если x1*= 40, то S1 = S0 –x1* = 60 – 40 = 20. Из таблицы при k = 2 и S1=20 находим в последнем столбце x2*= 0. Тогда S2 = S1 –x2* = 20 – 0 = 20. Действия при S2 = 20 рассмотрены выше.
Получаем еще два оптимальных варианта распределения средств: x1*=40, x2*= 0, x3*= 0, x4*= 20 и x1*= 40, x2*= 0, x3*= 20, x4*= 0.
Для наглядности сведем оптимальные решения в таблицу.
| x1* | x2* | x3* | x4* |
Общий прирост выпуска продукции в каждом из вариантов равен 37 млн. руб.
| x1* | x2* | x3* | x4* |
Лекция №16-17 Методы теории игр
Как уже говорилось выше, во многих ситуациях принятие хозяйственных решений приходится осуществлять в условиях неопределенности второго порядка. Подобные ситуации называют игровыми. Их суть состоит в том, что принятие решения приходится осуществлять в условиях, когда в этом процессе принимает участие несколько сторон, причем часто с противоположными интересами, например, как в классической ситуации взаимодействия продавца и покупателя. Иными словами, это ситуации, в которых возникает конфликт интересов. Эти ситуации называют игровыми, а участников игроками. Если интересы игроков строго антагонистичны, то игры называют антагонистическими, если в процессе игры участники могут каким-либо образом объединяться, что сулит им более высокие выигрыши, то игры называются кооперативными. Конфликт может возникать не только в результате сознательных действий различных участников, но и в результате действия тех или иных «стихийных сил». В последнем случае говорят об «играх с природой». Для характеристики игровой ситуации используются следующие понятия: «игроки» — множество заинтересованных сторон, которых также называют участниками, сторонами, лицами; «стратегии» — возможные действия каждой из сторон; «функции выигрыша» или «платежи» — числовые характеристики, выражающие интересы игроков. Стратегии бывают «чистыми» и «смешанными». Чистая стратегия — это стратегия, ориентированная на определенное поведение игрока-противника. Смешанная стратегия — это стратегия, ориентированная на несколько возможных стратегий поведения игрока-противника.
Классифицируют игры по разным признакам: по числу игроков, по числу стратегий, по свойствам функции выигрыша, по возможности предварительных переговоров и взаимодействия между игроками в ходе игры.
По числу игроков различают игры с двумя, тремя и большим количеством игроков.
По количеству стратегий различают конечные и бесконечные игры. В конечных играх игроки располагают конечным числом стратегий, в бесконечных — бесконечным.
По свойствам функций выигрыша различают игры с нулевой суммой (антагонистические), т. е. игры, в которых есть прямой конфликт и выигрыш одного участника равен проигрышу второго, и игры с постоянной разностью, т. е. такие, в которых игроки проигрывают и выигрывают одновременно.
В зависимости от возможности предварительных переговоров между игроками различают кооперативные и некооперативные игры.
Для формулировки задачи в игровой постановке необходимо реализовать следующие этапы.
1-й этап. Определение участников игры (игроков).
На этом этапе анализируется условие задачи и делается попытка выделить участников игры, а также определить суть конфликта, который возникает между ними.
2-й этап. Определение стратегий игроков.
Определение стратегий игроков процесс во многом неформальный. Чтобы выделить стратегии, необходим
о сформулировать конечные цели игроков и найти пути достижения этих целей. В матричных играх с нулевой суммой цели игроков прямо противоположны.
3-й этап. Определение выигрышей игроков при использовании каждой стратегии.
Выигрыши (платежи) обязательно должны иметь количественное выражение. Выигрыши являются показателями степени достижения целей соответствующего игрока. Выигрыши определяются при сочетании различных стратегий игроков.
4-й этап. Представление матрицы выигрышей (платежей) в нормальной форме.
Представление осуществляется путем внесения найденных значений выигрышей (платежей) в матрицу.
Основным принципом решения матричных антагонистических игр является предположение о том, что каждый игрок стремится обеспечить себе максимально возможный выигрыш при любых действиях партнера. В этих условиях оптимальной стратегией игрока № 1 вне зависимости от стратегии противника будет стратегия, максимизирующая минимальный выигрыш, т. е. максиминная стратегия, а для игрока № 2 тогда оптимальной является минимаксная стратегия.
Фундаментальным результатом теории игр является Теорема о минимаксе, которая утверждает, что сформулированные задачи для игроков № 1 и 2 всегда имеют решение для любой матрицы выигрышей и решения совпадают.
Оптимальные стратегии легко находятся для небольших игр, но вычисления становятся достаточно сложными с ростом числа стратегий. Для поиска оптимальных стратегий используется несколько приемов.
Первый прием состоит в уменьшении размерности игры за счет определения доминирующих строк и столбцов в платежной матрице. Доминирующим столбцом (строкой) называется столбец, в котором все выигрыши не меньше выигрышей в некотором другом столбце. Отсюда следует, что доминируемый столбец может быть заведомо удален из дальнейшего рассмотрения.
Второй подход состоит также в упрощении матрицы выигрышей за счет того, что аффинное преобразование матрицы платежей (т. е. преобразование всех элементов платежной матрицы по правилу W* = a W + b, a ≠ 0) не изменяет решения игры. Это свойство используется для упрощения и придания наглядности матрице выигрышей (платежей).
Рассмотрим пример одноходовой антагонистической игры.
Задача
Предприятие выпускает два вида скоропортящихся продуктов А и В. Себестоимость единицы А составляет 8 руб., а отпускная цена — 12 руб. Себестоимость единицы В равна 5 руб., отпускная цена — 8 руб. Если продукция не реализуется в день выпуска, то ее качество резко снижается и она продается на следующий день по цене в четыре раза ниже отпускной. Реализация продукции зависит от погоды: в хорошую погоду реализуется 2500 ед. продукции А и 15 000 ед. продукции В, а вплохую — 10 000 ед. продукции А и 3000 ед. продукции В. На реализацию всей продукции в день расходуется 5000 руб. Определить ежедневное производство продукции каждого вида с целью получения наибольшей прибыли.
Сведем исходные данные в табл. 5.2.
Таблица 5.2
| Товар | Себестоимость | Цена 1 | Цена 2 | Хорошая погода | Плохая погода | Затраты на реализацию |
| А | ||||||
| В |
Решение
В данном случае очевидно: первый игрок — предприятие, второй — природа.
Очевидно также, что у предприятия две чистые стратегии: первая — ориентация на хорошую погоду, вторая — на плохую. У природы также две стратегии: «быть» хорошей или плохой.
Определим выигрыши предприятия при использовании чистых стратегий. Выигрыш — это прибыль, которая определяется как разность между суммарной реализацией и затратами.
Затраты при первой чистой стратегии составляют:
С1 = 8∙2500 + 5∙15 000 + 5000 = 100 000 руб.
Затраты при второй стратегии:
С2= 8∙10 000 + 5∙3000 + 5000 = 100 000 руб.
Реализация зависит от природы.
Если предприятие реализует первую стратегию и природа первую стратегию, то объем реализации составит:
Р11 = 12∙2500 + 8∙15 000 = 150 000 руб.
Если предприятие реализует первую стратегию, а природа вторую, то объем реализации составит: Р12= 12∙2500 + 8∙3000 + 2∙12 000 = 78 000 руб.
Если предприятие реализует вторую стратегию, а природа первую, то объем реализации составит: Р21 = 12∙2500 + 8∙3000 + 3∙7500 = 76 500 руб.
Если предприятие реализует вторую стратегию и природа вторую, то объем реализации составит: Р22 = 12∙10 000 + 8∙3000 = 144 000 руб.
Определим прибыль предприятия для каждого сочетания стратегий:
П11 = 150 000 руб. - 100 000 руб. = 50 000 руб.;
П12 = 78 000 руб. - 100 000 руб. = 22 000 руб.;
П21 =76 500 руб. - 100 000 руб. = -23 5000 руб.;
П22 = 144 000 руб. - 100 000 руб. = 44 000 руб.
Платежная матрица или матрица выигрышей имеет вид:
| Стратегии предприятия | Стратегии природы | |
| 50000 руб. | -22000 руб. | |
| -235000 руб. | 44000 руб. |
Определяются нижняя и верхняя чистые цены игры. Нижняя цена игры определяется по формуле:
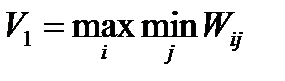
где Wij — выигрыш при i-й стратегии первого игрока (предприятия) и j-йстратегии второго.
Верхняя цена игры определяется по формуле:
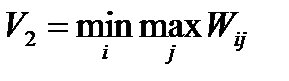
Если нижняя и верхняя цены игры совпадают, то игра имеет седловую точку и решается в чистых стратегиях. Если нижняя и верхняя цены игры не равны, то игра решается в смешанных стратегиях.
Для нашей задачи V1 = -22 000 руб., V2 = 44 000 руб. и V1 ≠ V2, поэтому решение в чистых стратегиях невозможно, следовательно, нужно искать решение в смешанных стратегиях.
Список литературы
1. Общий курс высшей математики для экономистов / Под ред. В. И. Ермакова. М.: Инфра-М, 1999.
2. Сборник задач по высшей математике для экономистов / Под ред. В. И. Ермакова. М.: Инфра-М, 2001.
3. Кузнецов Ю. Н., Кузубов В. И., Волощенко А. Б. Математическое программирование. М.: Высшая школа, 1980.
4. Ляшенко И. Н., Карагодова Е. А., Черникова Н. В., Шор Н. З. Линейное и нелинейное программирование / Под ред. проф.
И. Н. Ляшенко. Киев: Вища школа, 1975.
5. Калихман И. Л. Линейная алгебра и программирование. М.: Высшая школа, 1967.
6. Калихман И. Л. Сборник задач по математическому программированию. М.: Высшая школа, 1975.
7. Акулич И. Л. Математическое программирование в примерах и задачах. М.: Высшая школа, 1975.
8. Матвеев В. И., Сагитов Р. В., Шершнев В. Г. Курс линейного программирования для экономистов. М.: Менеджер, 1998.
Дата добавления: 2017-05-18; просмотров: 1383;
