Особенности решения транспортных задач с неправильным балансом

До сих пор рассматривались транспортные задачи с правильным балансом. Однако на практике чаще встречаются задачи с неправильным балансом. Каковы особенности их решения?

1. Пусть суммарные запасы поставщиков превосходят суммарные запросы потребителей, т. е.

.

Очевидно, что в этом случае при составлении оптимального плана перевозок часть запасов поставщиков, равная

,

останется не вывезенной. Поэтому в системе ограничений транспортной задачи первую группу уравнений (6.2) следует заменить неравенствами

, i = 1, 2, ..., m. (6.15)

Вторая группа уравнений остается без изменения, так как запросы всех потребителей удовлетворяются полностью. Для приведения к канонической форме в неравенства (6.15) вводят дополнительные переменные . В результате первые m ограничений задачи принимают вид

, i = 1, 2, ..., m.

В целевую функцию дополнительные переменные не входят (входят с нулевыми коэффициентами). Математическая модель задачи принимает вид

, (6.16)

, i = 1, 2, ..., m, (6.17)

, j = 1, 2, ..., n, (6.18)

, i = 1, 2, ..., m; j = 1, 2, ..., n+1. (6.19)

Запишем необходимое и достаточное условие разрешимости задачи (теорема 6.1)

.

Отсюда получаем

.

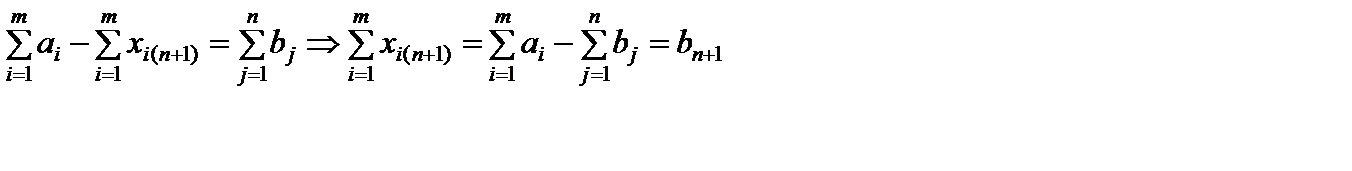Следовательно, чтобы задача в рассматриваемом случае имела решение, необходимо ввести фиктивного потребителя с запросами , равными разности суммарных запасов поставщиков и запросов потребителей, и нулевыми стоимостями перевозок единиц груза .

2. Аналогично в случае, когда суммарные запросы потребителей превосходят суммарные запасы поставщиков, т. е.

,

часть запросов потребителей, равная

,

останется не удовлетворенной. Поэтому вторая группа уравнений системы ограничений задачи (6.3) заменяется неравенствами

, j = 1, 2, ..., n.

После введения в эти неравенства дополнительных переменных математическая модель задачи примет вид

, (6.20)

, i = 1, 2, ..., m, (6.21)

, j = 1, 2, ..., n, (6.22)

, i = 1, 2, ..., m+1; j = 1, 2, ..., n. (6.23)

Для того чтобы задача имела решение, необходимо и достаточно, чтобы

.

Отсюда получаем

.

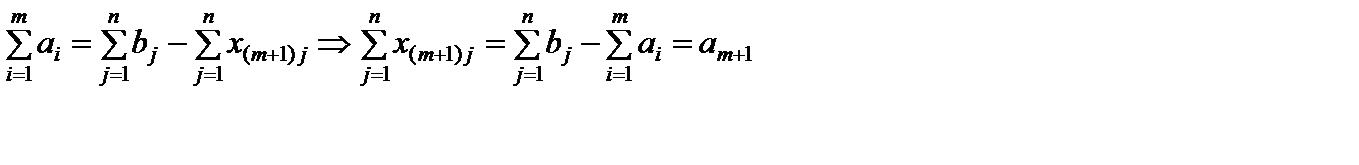Следовательно, чтобы в этом случае задача имела решение, необходимо ввести фиктивного поставщика с запасами , равными разности суммарных запросов потребителей и запасов поставщиков, и нулевыми стоимостями перевозок единиц грузов .

Необходимо отметить, что при составлении начального опорного решения в последнюю очередь следует распределять запасы фиктивного поставщика и удовлетворять запросы фиктивного потребителя, несмотря на то, что им соответствует наименьшая стоимость перевозок, равная нулю.