Переход от одного опорного решения к другому

В транспортной задаче переход от одного опорного решения к другому осуществляется с помощью цикла. Для некоторой свободной клетки таблицы строится цикл, содержащий часть клеток, занятых опорным решением. По этому циклу производится перераспределение объемов перевозок. Загружается перевозка в выбранную свободную клетку и освобождается одна из занятых клеток, получается новое опорное решение.

Теорема 6.6 (о существовании и единственности цикла). Если таблица транспортной задачи содержит опорное решение, то для любой свободной клетки таблицы существует единственный цикл, содержащий эту клетку и часть клеток, занятых опорным решением.

Доказательство. Опорное решение занимает N = m + n -1 клеток таблицы, которым соответствуют линейно независимые векторы условий. Согласно теореме 6.3 никакая часть занятых клеток не образует цикл. Если же к занятым клеткам присоединить одну свободную, то соответствующие им m + n векторы – линейно зависимые, и по той же теореме существует цикл, очевидно, содержащий эту клетку. Предположим, что таких циклов два и . Тогда, объединив клетки обоих циклов без свободной клетки , получим последовательность клеток

, ,

которые образуют цикл. Это противоречит линейной независимости векторов условий, образующих базис опорного решения.

Означенный цикл

Цикл называется означенным, если его угловые клетки перенумерованы по порядку и нечетным клеткам приписан знак "+", а четным – знак "-" (рис. 6.2).

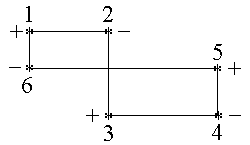
Рис 6.2

Сдвигом по циклу на величину q называется увеличение объемов перевозок во всех нечетных клетках цикла, отмеченных знаком "+", на q и уменьшение объемов перевозок во всех четных клетках, отмеченных знаком "-", на q.

Теорема 6.7. Если таблица транспортной задачи содержит опорное решение, то при сдвиге по любому циклу, содержащему одну свободную клетку, на величину получится опорное решение.

Доказательство. В таблице транспортной задачи, содержащей опорное решение, выберем свободную клетку и отметим ее знаком "+". По теореме 6.6 для этой клетки существует единственный цикл, который содержит часть клеток, занятых опорным решением. Перенумеруем клетки цикла, начиная с клетки, отмеченной знаком "+". Найдем и осуществим сдвиг по циклу на эту величину.

В каждой строке и в каждом столбце таблицы, входящих в цикл, две и только две клетки, одна из которых отмечена знаком "+", а другая - знаком "-". Поэтому в одной клетке объем перевозки увеличивается на q, а в другой уменьшается на q, при этом сумма всех перевозок в строке (или столбце) таблицы остается неизменной. Следовательно, после сдвига по циклу по-прежнему и запасы всех поставщиков вывозятся полностью, и запросы всех потребителей удовлетворяются полностью. Так как сдвиг по циклу осуществляется на величину , то все объемы перевозок будут неотрицательными. Следовательно, новое решение является допустимым.

Если оставить свободной одну из клеток с нулевым объемом перевозки, соответствующих , то число занятых клеток будет равно N = m + n -1.

Одна клетка загружается (отмеченная знаком "+"), одна – освобождается. Так как цикл единственный, то удаление из него одной клетки разрывает его. Цикл из оставшихся занятых клеток образовать нельзя, соответствующие векторы-условия линейно независимы, а решение является опорным.