Методы построения начального опорного решения. Метод северо-западного угла

Существует ряд методов построения начального опорного решения, наиболее простым из которых является метод северо-западного угла. В данном методе запасы очередного поставщика используются для обеспечения запросов очередных потребителей до тех пор, пока не будут исчерпаны полностью, после чего используются запасы следующего по номеру поставщика.

Заполнение таблицы транспортной задачи начинается с левого верхнего угла и состоит из ряда однотипных шагов, на каждом из которых, исходя из запасов очередного поставщика и запросов очередного потребителя, заполняется только одна клетка и соответственно исключается из рассмотрения один поставщик или потребитель. Осуществляется это по следующим правилам:

1) если то и исключается поставщик с номером i, ;

2) если то и исключается потребитель с номером j, ;

3) если то и исключается либо поставщик с номером i, , либо потребитель с номером j, .

Нулевые перевозки принято заносить в таблицу только в том случае, когда они попадают в клетку с номером (i, j), подлежащую заполнению. Если в очередную клетку таблицы (i, j) требуется поставить перевозку, а поставщик с номером i или потребитель с номером j имеет нулевые запасы или запросы, то ставится в клетку перевозка, равная нулю (базисный нуль), и после этого обычным образом исключается из рассмотрения соответствующий поставщик или потребитель. Таким образом, в таблицу заносятся только базисные нули, остальные клетки с нулевыми перевозками остаются пустыми.

Во избежание ошибок после построения начального опорного решения необходимо проверить, что число занятых клеток равно , и векторы-условия, соответствующие этим клеткам, линейно независимы.

Теорема 6.4. Решение транспортной задачи, построенное по методу северо-западного угла, является опорным.

Доказательство. Число занятых опорным решением клеток таблицы должно быть равно . На каждом шаге построения решения по методу северо-западного угла заполняется одна клетка и исключается из рассмотрения одна строка (поставщик) или один столбец (потребитель) таблицы задачи. Через шага в таблице будет занято клетки. В то же время останутся не вычеркнутыми одна строка и один столбец, а клетка одна. При заполнении этой последней клетки число занятых клеток составит

.

Проверим, что векторы, соответствующие занятым этим решением клеткам, являются линейно независимы. Применим метод вычеркивания. Все занятые клетки можно вычеркнуть, если проделать это в порядке их заполнения.

Необходимо иметь в виду, что метод северо-западного угла не учитывает стоимость перевозок, поэтому опорное решение, построенное данным методом, может быть далеким от оптимального.

Пример 6.2. Составить начальное опорное решение, используя метод северо-западного угла, для транспортной задачи, исходные данные которой представлены в табл. 6.3.

Т а б л и ц а 6.3

Решение. Распределяем запасы 1-го поставщика. Так как его запасы меньше запросов первого потребителя , то в клетку (1, 1) записываем перевозку и исключаем из рассмотрения поставщика. Определяем оставшиеся неудовлетворенными запросы 1-го потребителя .

Распределяем запасы 2-го поставщика. Так как его запасы больше, оставшихся неудовлетворенными запросов 1-го потребителя , то в клетку (2, 1) записываем перевозку и исключаем из рассмотрения 1-го потребителя. Определяем оставшиеся запасы 2-го поставщика . Так как , то в клетку (2, 2) записываем и исключаем по своему усмотрению либо второго поставщика, либо второго потребителя. Пусть исключили 2-го поставщика. Вычисляем оставшиеся неудовлетворенными запросы второго потребителя =200 - 200 = 0.

Распределяем запасы 3-го поставщика. Так как
(200 > 0), то в клетку (3, 2) записываем и исключаем второго потребителя. Запасы третьего поставщика не изменились 200-0 =200. Сравниваем и (200 > 100), в клетку (3, 3) записываем , исключаем 3-го потребителя и вычисляем 200 - 100 = 100. Так как , то в клетку (3, 4) записываем . Ввиду того, что задача с правильным балансом, запасы всех поставщиков исчерпаны и запросы всех потребителей удовлетворены полностью и одновременно.

Результаты построения опорного решения приведены в
табл. 6.4.

Т а б л и ц а 6.4

Проверяем правильность построения опорного решения. Число занятых клеток должно быть равно . В табл. 6.4 занято 6 клеток. Применяя метод вычеркивания, убеждаемся, что найденное решение является вычеркиваемым (звездочкой отмечен базисный нуль).

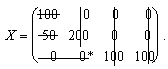
Следовательно, векторы-условий, соответствующие занятым клеткам, линейно независимы и построенное решение действительно является опорным.