Метод минимальной стоимости

Метод минимальной стоимости прост и позволяет построить опорное решение, достаточно близкое к оптимальному, так как использует матрицу стоимостей транспортной задачи ,
i = 1, 2, ..., m; j = 1, 2, ..., n. Как и метод северо-западного угла, он состоит из ряда однотипных шагов, на каждом из которых заполняется только одна клетка таблицы, соответствующая минимальной стоимости , и исключается из рассмотрения только одна строка (поставщик) или один столбец (потребитель). Очередную клетку, соответствующую , заполняют по тем же правилам, что и в методе северо-западного угла. Поставщик исключается из рассмотрения, если его запасы груза использованы полностью. Потребитель исключается из рассмотрения, если его запросы удовлетворены полностью. На каждом шаге исключается либо один поставщик, либо один потребитель. При этом, если поставщик еще не исключен, но его запасы равны нулю, то на том шаге, когда от данного поставщика требуется поставить груз, в соответствующую клетку таблицы заносится базисный нуль и лишь затем поставщик исключается из рассмотрения. Аналогично с потребителем.

Теорема 6.5. Решение транспортной задачи, построенное по методу минимальной стоимости, является опорным.

Доказательство аналогично доказательству опорности решения, построенного по методу северо-западного угла.

Пример 6.3. Используя метод минимальной стоимости, построить начальное опорное решение транспортной задачи, исходные данные которой приведены в табл. 6.5.

Т а б л и ц а 6.5

Решение. Запишем отдельно матрицу стоимостей для того, чтобы удобнее было выбирать минимальные стоимости, вычеркивать строки и столбцы.

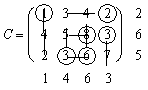
Среди элементов матрицы стоимостей выбираем наименьшую стоимость , отмечаем ее кружочком. Данная стоимость имеет место при перевозке груза от 1-го поставщика 1-му потребителю. В соответствующую клетку (1, 1) записываем максимально возможный объем перевозки (табл. 6.6).

Т а б л и ц а 6.6

Запасы 1-го поставщика уменьшаем на 40, т. е. Исключаем из рассмотрения 1-го потребителя, так как его запросы удовлетворены. В матрице С вычеркиваем 1-й столбец.

В оставшейся части матрицы С минимальной является стоимость .

Максимально возможная перевозка, которую можно осуществить от 1-го поставщика 4-му потребителю равна . В соответствующую клетку таблицы записываем перевозку . Запасы первого поставщика исчерпаны, исключаем его из рассмотрения. В матрице С вычеркиваем первую строку. Запросы 4-го потребителя уменьшаем на 20, .

В оставшейся части матрицы С минимальная стоимость . Заполняем одну из двух клеток таблицы (2, 4) или (3, 2). В клетку (2, 4) запишем . Запросы 4-го потребителя удовлетворены, исключаем его из рассмотрения, вычеркиваем 4-й столбец в матрице С. Уменьшаем запасы 2-го поставщика 80 - 40 = 40.

В оставшейся части матрицы С . Запишем в клетку таблицы (3, 2) перевозку . Исключим из рассмотрения 2-го потребителя, а из матрицы С 2-й столбец. Вычисляем .

В оставшейся части матрицы С наименьшая стоимость . Запишем в клетку таблицы (3, 3) перевозку = 40. Исключим из рассмотрения 3-го поставщика, а из матрицы С 3-ю строку. Определяем
.

В матрице С остался единственный элемент . Записываем в клетку таблицы (2, 3) перевозку .

Проверяем правильность построения опорного решения. Число занятых клеток таблицы равно N = m + n - 1 = 3 + 4 - 1 = 6 (табл. 6.6). Методом вычеркивания проверяем линейную независимость векторов-условий, соответствующих положительным координатам решения. Порядок вычеркивания показан на матрице Х.

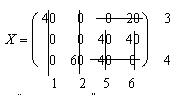
Решение является вычеркиваемым и, следовательно, опорным.