Системы проводников

В системе нескольких заряженных проводников потенциал каждого проводника определяется не только зарядом данного тела, но также и зарядами всех остальных тел. При этом потенциал является линейной функцией зарядов.

Потенциалы тел могут быть найдены методом наложения. Тогда, например, для системе двух проводящих тел имеем уравнения.

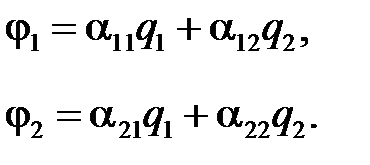
Здесь 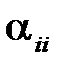― собственный потенциалный коэффициент; 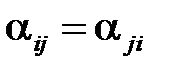― взаимные потенциалные коэффициенты.

Решая приведенные выше уравнения относительно зарядов, получим

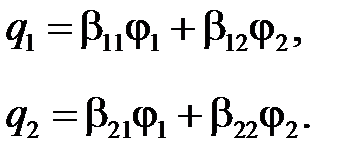
Коэффициенты 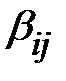называются коэффициентами электростатической индукции ― собственными при одинаковых индексах и взаимными при разных индексах. Собственные коэффициенты ― положительные, взаимные ― отрицательные.

Применяются также уравнения, когда заряд каждого тела выражают через разность потенциалов данного тела и других тел, в том числе и земли.

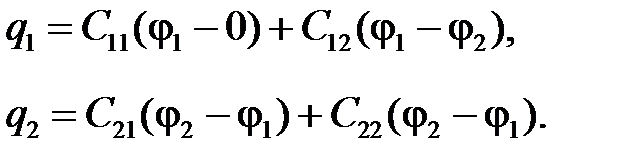
Коэффициенты 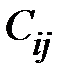называются частичными емкостями ёмкостями ― собственными при одинаковых индексах и взаимными при разных индексах.

2.10.10. Поле и емкость ёмкость двухпроводной линии с учетом влияния земли

Двадлинных провода расположенны параллельно проводящей плоскости (над землею). Радиусы проводов 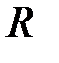высоты подвесок 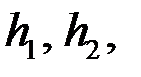межосевое расстояние 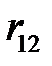при этом h_1,2>>R, d>>R₂. Известны .

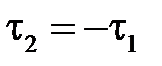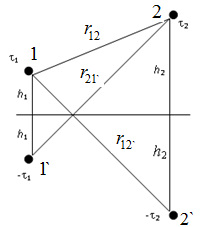
Рис.2.15. Двухпроводная линия

Применим метод зеркальных изображений. Заменим проводящую среду (землю) диэлектриком с 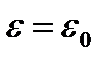, а поверхностные заряды земли — системой зеркальных зарядов проводов с противоположными знаками. Смещением электрических осей пренебрегаем, так как по условию h>>R.

Потенциалы проводов можно определить через линейные плотности зарядов, применяя метод наложения:

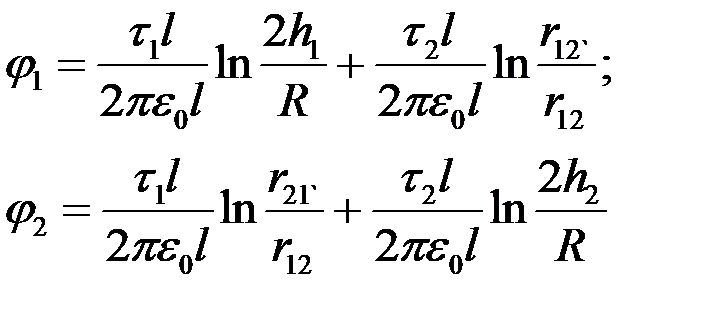
или

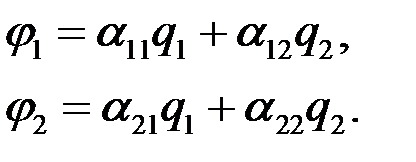(2.12)

Здесь обозначены:

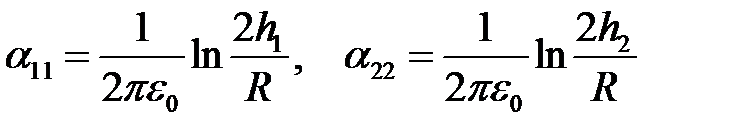- собственные потенциальные коэффици­енты;

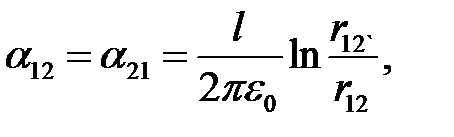- взаимные потен­циальные коэффициенты.

Рассчитаем рабочую емкость двухпроводной линии.

Имеем для первого про­вода 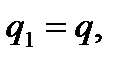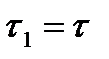, для второго про­вода 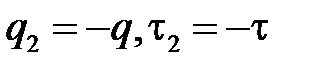. Тогда получим:

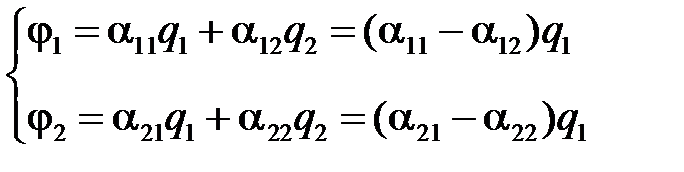
Напряжение между проводами:

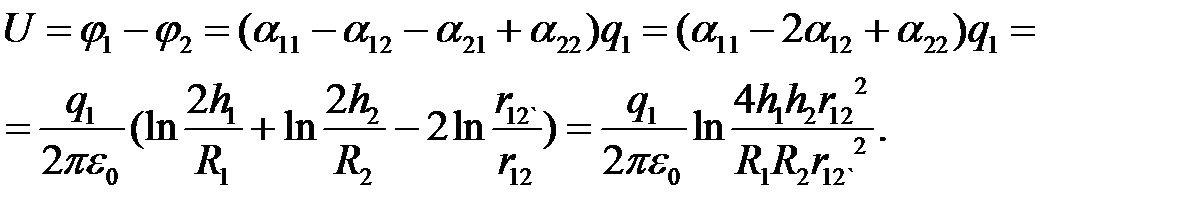
Откуда следует формула емкости ёмкости линии с учетом влияния земли:

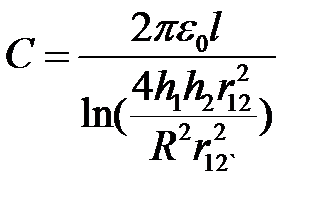,[Ф/м].

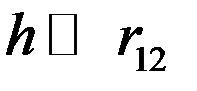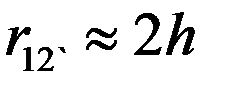Если линия расположена достаточно высоко над землей ( ), то и выражение для рабочей емкости превращается в выражение емкости ёмкости линии без учета влияния земли .

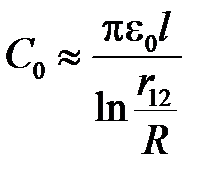Задача.

Двухпроводная воздушная линия,отключенная от источника,находится в однородном поле грозовой тучи с Напряжённостью 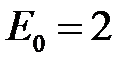кВ/м, направленного перпендикулярно поверхности земли (рис.2.16).

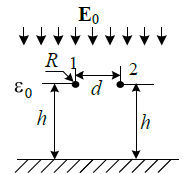
Рис.2.16. Электрическое поле грозовой тучи

Провод 1 ― излирован; провод 2 ― заземлен. Высота подвеса проводов h = 5 м; растояние между ними d = 1, а их радиусы R = 1 см.

Найти потенциал первого провода.

Решение.

Потенциалы проводов определяются внешним полем и

индуцированными зарядами на проводах.

.

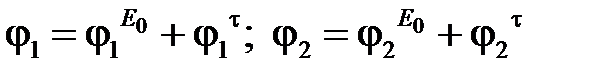Поскольку провода подвешены на одной высоте, то .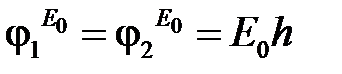

Так как первый провод изолирован, а линия была отключена от источника, заряд на нем равен нулю τ₁=0.Поэтому имеем:

,

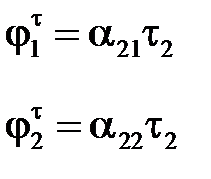где 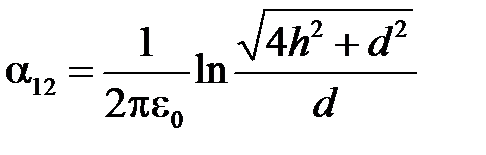, 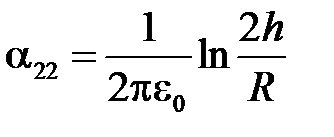- потенциальные коэффициенты.

С учетом поля тучи имеем:

.

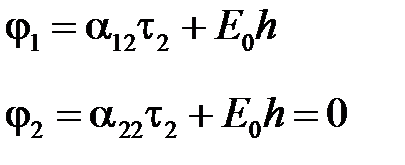Решая относительно 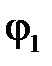, получим

.

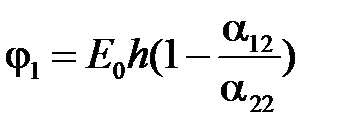Подставив числовые данные, получим 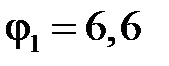кВ.

2.10.11. Электрическое поле и емкость ёмкость трехфазной линии

По­лученные ранее соотношения для двух­проводной линии в статическом режиме с большой степенью точности могут быть применены к расчёту поля линий электропередач перемен­ного тока на промышленной частоте f = 50 Гц. Критерием допустимости приближенного рассмотрения переменного электрического поля около проводов линии в отдельные моменты времени как элетростатического может служить соотношение между линейными размерами области и длиной электромагнитной волны. В воздухе при частоте 50 Гц скорость волны равна 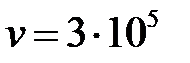м/с, а длина равна 6000 км. На длине волны фаза колебаний поля меняется на 2π. В пределах области, линейные размеры которой значительно меньше λ, можно считать фазу колебаний напряженности поля одинаковой во всех точках области и с большой степенью точности рассматривать поля в каждый момент времени как электостатическое.

В уравнениях, связывающих заряды и потенциалы, необходимо под q и j понимать в этом случае мгновенные заряды проводов и мгновенные напряжения между проводами и землей (фазные напряже­ния). При синусоидальном процессе эти уравнения могут быть записаны в символической форме для комплексов действующих значений зарядов и напряжений.

;

.

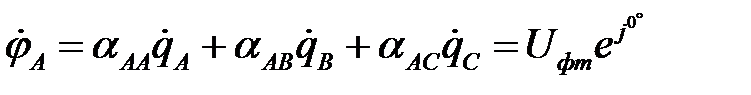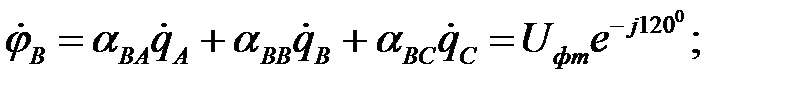
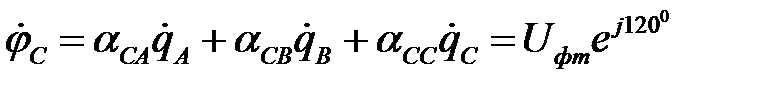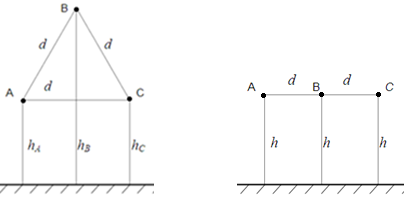
Для трехфазных линий применяются различные варианты расположения проводов в пространстве. Провода могут быть расположены вершинам рав­ностороннего треугольника (рис.2.16а17а). В этом случае равны

а) б)

Рис.2.1617

расстояния между проводами ( 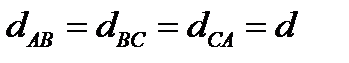), но не равны их высоты над землей ( 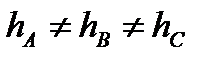). Во втором варианте (рис.2.16б17б) не равны расстояния между проводами ( 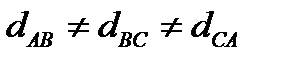), но равны их высоты над землей ( ).

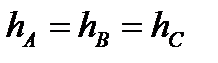Таким образом, в воз­душных трехфазных ЛЭП не может быть достигнута полная симметрия проводов в про­стран­стве. Потенциальные коэффициенты 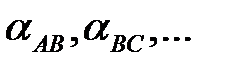, которые определяются через геометриче­ские расстояния, будут разными.

Несимметрия потенциальных коэффи­циентов вызо­вет несимметрию зарядов проводов 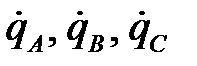и соответствующую несиммет­рию зарядных токов линии 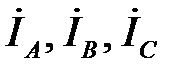в режиме хо­лостого хода. Полная сим­метрия проводов в пространстве достигается только в кабельных линиях.

Для устранения несимметрии фаз воздушных линий электропередачи че­рез равные расстояния (обычно через 1/3 длины линии) производят круговую переста­новку или транспозицию проводов.

При наличии транспозиции (рис.2.1718) усред­ненные значения параметров линии полу­чаются одинаковыми для всех фаз, при этом несимметрия между началом и концом линии устраняется.

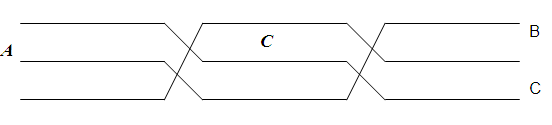
Рис.2.17

Средние значения потенциалов коэффициентов для транспонированной линии:

.

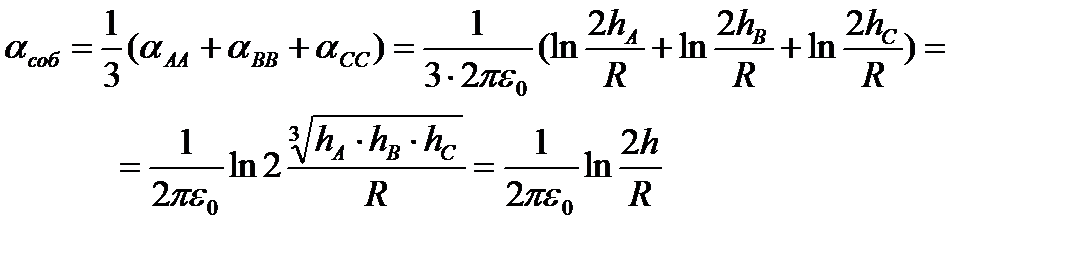
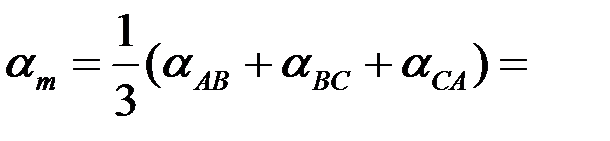
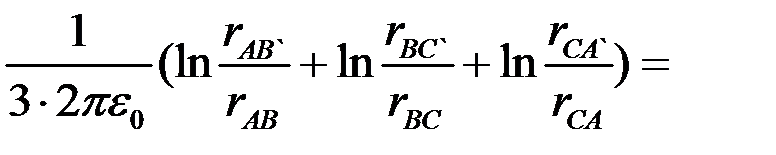
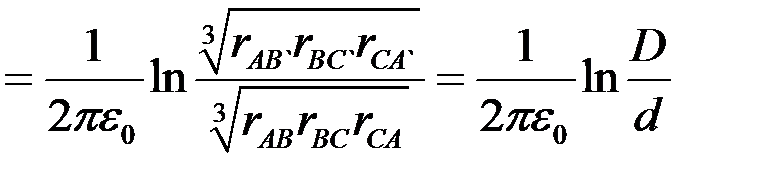где ; ; .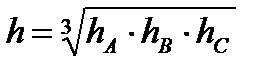

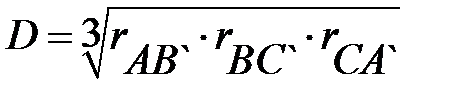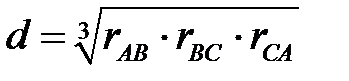Потенциальное уравнение для провода фазы А транспонированной линии получит вид:

.

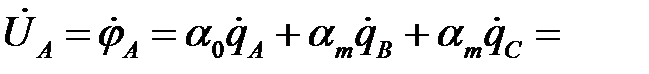
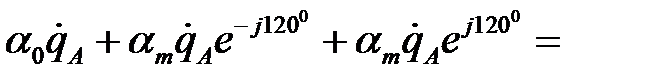
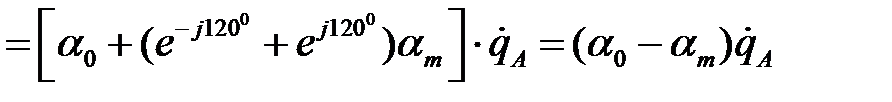Из полученного выражения следует формула для удельной емкости фазы ЛЭП на землю:

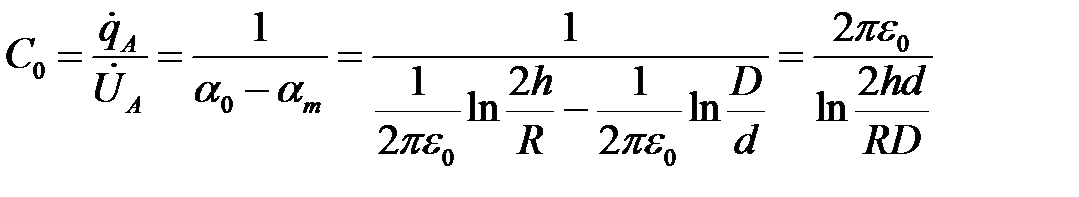, [Ф/м].

2.11. Метод средних потенциалов для расчёта потенциальных коэффициентов и емкостей ёмкостей в системе проводов

В электростатическом поле потенциал проводника одинаков во всех его точках, заряд же распределяется по поверхности проводника неравномерно.

В методе методом средних потенциалов полагается, что заряд распределяется равномерно по поверхности проводников и для линейных проводников — равномерно по их длине. Вычисляется распределение потенциала по поверхности или по длине проводников, и в формулу для емкости вводится среднее значение вычисленных таким образом потенциалов проводников. Этот метод в ряде случаев, например при вычислении емкости системы, образованной параллельными проводами, дает достаточно точные результаты. Объясняется это тем, что неравномерность распределения заряда заметно сказывается лишь на концах таких проводов.

Предположим, что имеются два отрезка проводов, длины которых l₁ и l₂ (рис.2.18). Требуется вычислить потенциальный коэффициент α₁₂. Предположим, что q₁ = 0 и q₂ = 0. При этом имеем 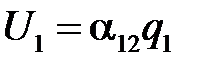. Полагаем, что заряд q₂ распределен равномерно вдоль второго провода с линейной плотностью τ₂ = q₂/l₂.

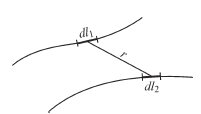
Рис.2.18

Потенциал в некоторой точке первого провода, определяемый зарядом q₂, будет равен

.

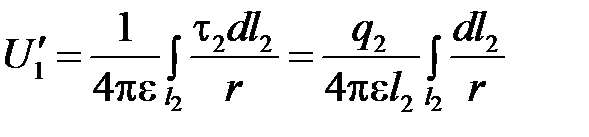причем интегрирование производится вдоль всего второго провода. Среднее значение потенциала первого провода получается в результате интегрирования вдоль первого провода:

.

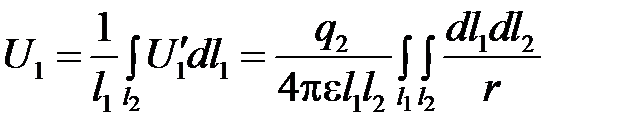Таким образом, искомый потенциальный коэффициент определяется формулой

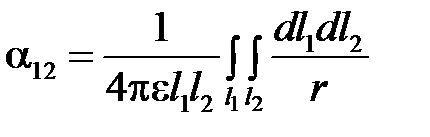
Выражение для потенциального коэффициента с одинаковыми индексами, например α₁₁ для прямолинейного отрезка провода круглого сечения, может быть найдено путем следующих рассуждений. Предполагаем соответственно принятому допущению, что заряд, находящийся на поверхности провода, равномерно распределен по длине провода. Находим потенциал 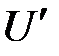, создаваемый этим зарядом в разных точках оси провода, и вычисляем среднее значение U потенциала вдоль оси. Пусть r — расстояние от кольцевого элемента поверхности проводника, имеющего длину 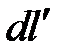в направлении оси проводника (рис.2.19), до элемента dl оси проводника, l — длина проводника и r₀ — радиус его сечения. Потенциал 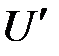в некоторой точке оси, определяемый всем зарядом q проводника, равен

.

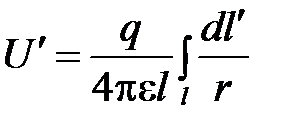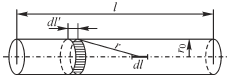
Рис.2.19

Среднее значение потенциала вдоль всей оси будет

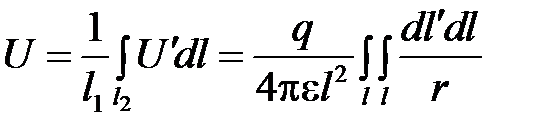
Следовательно,

.

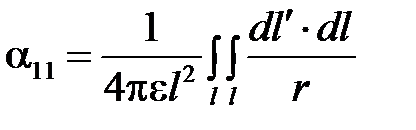причем наименьшее значение r есть r₀.

В качестве примера определим, пользуясь методом средних потенциалов, потенциальный коэффициент α₁₂ для параллельных отрезков проводов, расположенных на расстоянии D друг от друга и имеющих одинаковые длины l₁ = l₂ = l, причем начала отрезков лежат на одном перпендикуляре к ним. Оси координат расположим так, как показано на рис.2.20.

Имеем

.

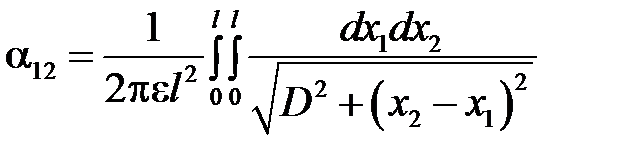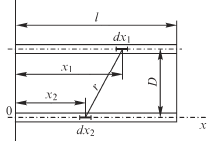
Рис.2.20

После вычислений, получим

.

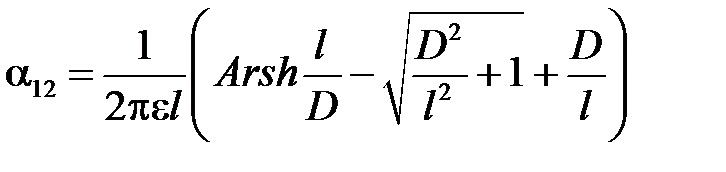При вычислении коэффициентов α₁₁ и α₂₂ с одинаковыми индексами для прямолинейного проводника, имеющего круглое сечение радиуса r₀, результат интегрирования приведет к формуле, которая получается из только что полученной формулы путем замены D на r₀. Следовательно,

.

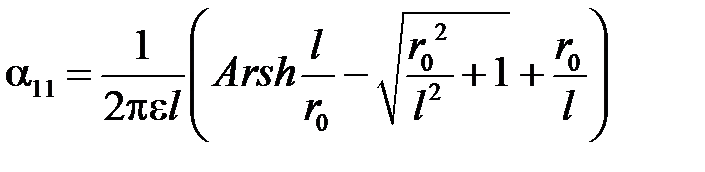Так как при выводе этой формулы наличие другого провода не учитывалось, то емкость уединенного цилиндра конечной длины получается из выражения

.

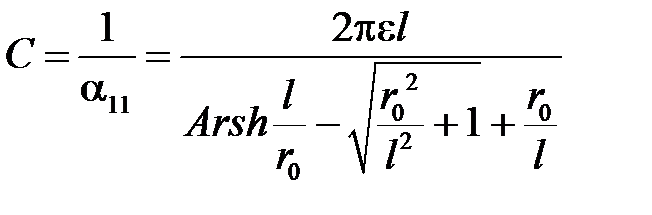Заметим, что имеет место соотношение

(*)

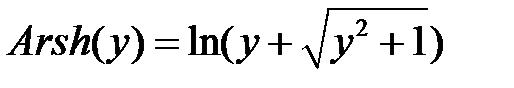С учетом (*) при 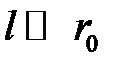будет

.

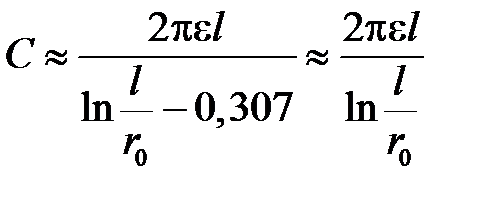Емкость между цилиндрами найдется:

,

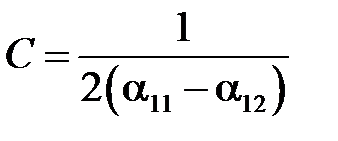где α₁₂ и α₁₁ находятся по только что полученным формулам.

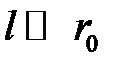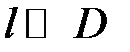При и имеем

.

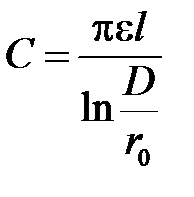Вопросы для самопроверки

1. Является ли электростатическое поле непрерывным?

2. Напишите уравнение, показывающее, что электрическое поле возникает в области, где расположен заряд. Дайте физическое толкование понятиям градиента и дивергенции.

3. Как изменяется напряженность электростатического поля при переходе из одной среды в другую?

4. Какие поля называют потенциальными?

6. Могут ли быть замкнутыми силовые линии в электростатическом поле?

7. Каким свойством обладает силовая трубка?

8. Изложите основные принципы графического построения картины поля?

Как по картине поля определить напряженность электрического поля? При решении каких задач целесообразно применять теоремуГаусса в интегральной форме?Какой радиус должен иметь уединенный металлический шар в воздухе, чтобы на нем можно было разместить заряд величиной 1 кулон? Пробивная напряженность воздуха 30 кВ/см.

9.

10. Какой физический смысл придается 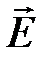и φ? Какая интегральная и дифференциальная связь существует между ними?

11. Определить модуль вектора напряженности электрического поля

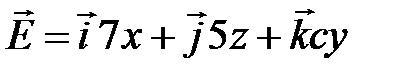,(В/м)

в точке с координатами x=2 (м), y=3 (м), z=4 (м).

13. Определить объемную плотность зарядовρ(мкКл/м3)

при потенциале: 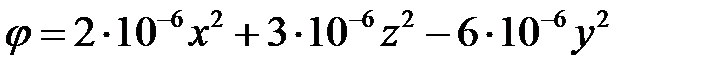,В.

2.