Электростатическое поле и емкость разноименно заряженных параллельных цилиндров. Поле двухпроводной линии
Разноименно заряженные параллельные цилиндры (рис.2.915) расположены в воздухе и имеют размеры R1; R2; D. Напряжение между цилиндрами U.
Заменим поверхностные заряды проводов осевыми +t и -t, проводящую среду — диэлектриком так, чтобы на поверхности «проводов» остались эквипотенциальными с теми же значениями потенциалов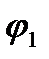 
и 
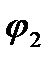. Тогда согласно второму следствию из теоремы единственности поле в диэлектрике не изменится. Чтобы выполнить эти условия, линейные заряды проводов должны быть смещены относительно геометрических осей цилиндров на некоторые расстояния 
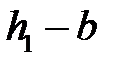и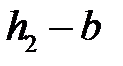 
. Положение линейных зарядов называют электрическими осями.
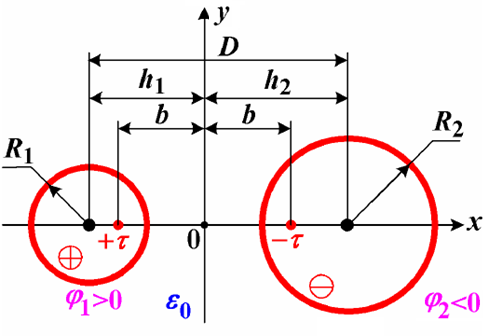
Рис.2.915. Заряженные параллельные цилиндры
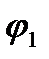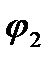Заменим поверхностные заряды проводов осевыми +t и -t, проводящую среду — диэлектриком так, чтобы на поверхности проводов сохранились прежние условия, а именно: эти поверхности должны остаться эквипотенциальными с теми же значениями потенциалов и . Тогда согласно второму следствию из теоремы единственности поле в диэлектрике не изменится. Чтобы выполнить эти условия, электрические оси проводов должны быть смещены относительно геометрических осей на некоторые расстояния 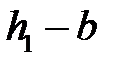и .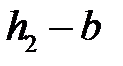
Для определения геометрических параметров имеем соотношения:
; 
; 
.
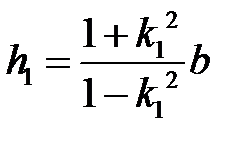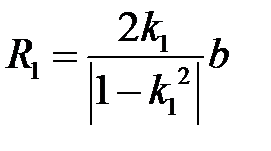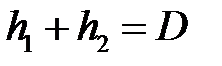Отсюда получаем: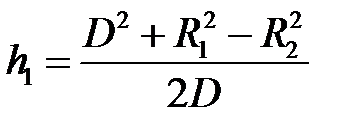 
.
Аналогично: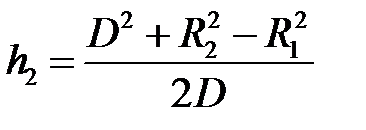 
.
.
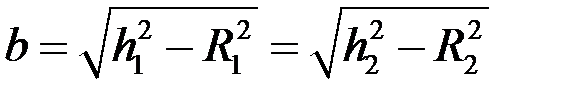Потенциал любой точки равен:
,
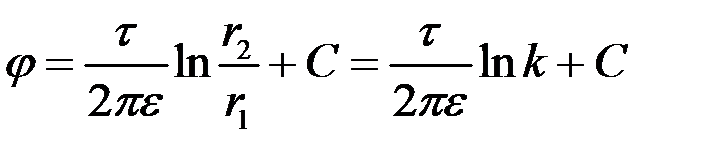где k ―- параметр линии потенциала при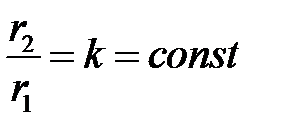 
.
Разность потенциалов цилиндров равна: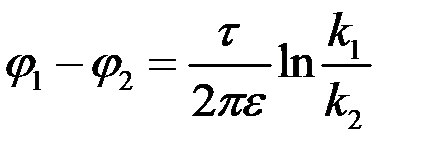 
.
Здесь k1 и k2 ― значение k для контуров сечений проводников, являющихся линями равного потенциала
Имеем:
.
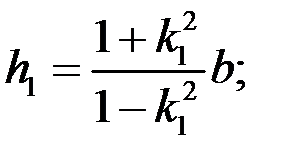
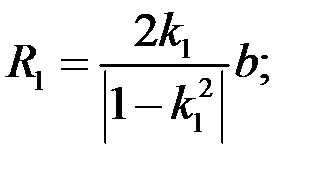
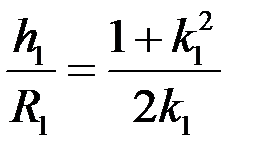Отсюда, учитывая, что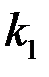 
>1, получаем 
.
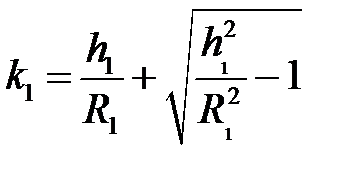Аналогично, учитывая, что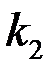 
<1;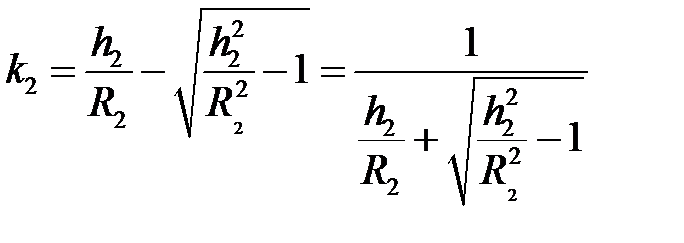 
.
Далее находим электрическую емкость цилиндров на единицу длиной lы:
.
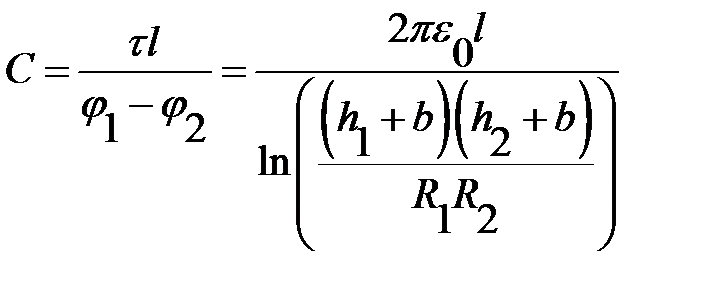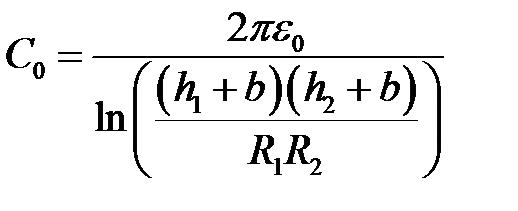
и линейную плотность зарядов: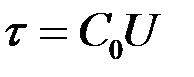 
.
Для двухпроводной линии h1=h2=h, R1=R 2=R. Тогда:
.
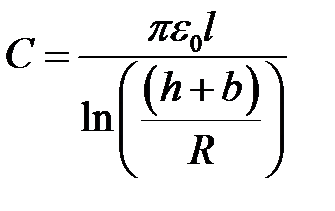Для воздушных линий межосевое расстояние D многократно больше радиуса проводов R. В этом случае смещением электрических осей можно пренебречь (h-b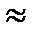 
0) и считать, что электрические оси проводов совпадают с геометрическими осями. Для таких линий полученные выше расчётные формулы будут иметь вид:
, 
.
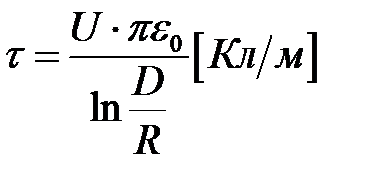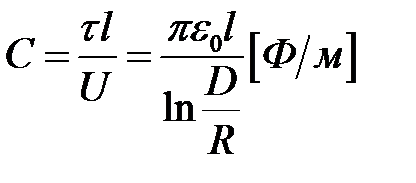Дата добавления: 2017-08-01; просмотров: 2034;