Плоскопараллельного поля

Во многих практических случаях форма сечений заряженных проводников и их взаимное расположение настолько сложны, что точный аналитический расчёт поля оказывается невозможным. В связи с этим получает практическое значение графический метод построения картины поля, который разработан для случаев плоскопараллельных полей и полей, окружающих заряженные тела вращения.

Наиболее просто построение осуществляется в случае плоскопараллельного поля. Должны быть соблюдены следующие условия:

1) линии напряженности поля и линии равного потенциала должны пересекаться всюду под прямым углом;

2) линии напряженности поля должны быть перпендикулярны к контурам, ограничивающим сечения проводников;

3) ячейки сетки, образованной линиями напряженности поля и линиями равного потенциал, при достаточной густоте сетки должны быть приблизительно подобны друг другу.

Третье условие соответствует требованию, чтобы приращение потенциала Dφ при переходе от любой линии равного потенциала к соседней было постоянным и чтобы поле было подразделено на трубки равного потока, т.е. чтобы было DV = const. Откуда и следует, что при достаточно густой сетке ее ячейки должны представлять собой приблизительно подобные прямоугольники, если форма ячейки не слишком искажена кривизной линий.

Обычно картину поля рисуют на глаз, стремясь удовлетворить первому и второму условиям, а затем уже постепенно вносят исправления так, чтобы удовлетворилось и третье условие. Рекомендуется для облегчения построения выбирать Dn = Dτ. На рис.2.21 в виде примера построено поле между двумя прямолинейными проводами прямоугольного сечения, имеющими одинаковые заряды разных знаков.

По картине поля можно в любой точке Напряжённость электрического поля в выбранной точке

.

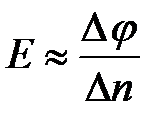где Dn ― расстояние между эквипотенциалями вблизи точки данной точки. При этом направление вектора Е задаем примерно посередине между силовыми линиями (см. рис. 2.921).

По картине поля можно также определять емкость между заряженными телами.

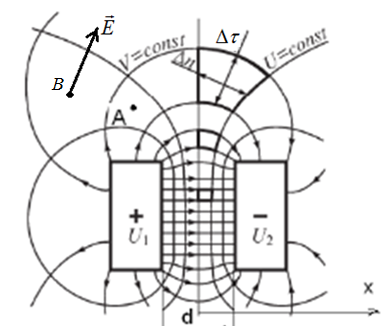
Рис.2.219

Емкость определяют по формуле

,

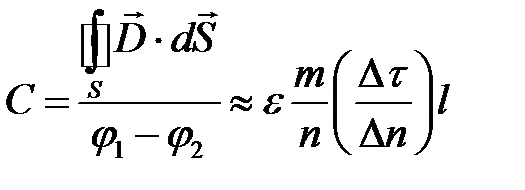где m ― число трубок поток потока; n ― число интервалов между линиями равного потенциала; 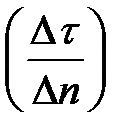― коэффициент формы ячеек поля; l ― длина.

2.10.2. Расчёт поля плоского конденсатора при наличии между