Способ плоскопараллельного перемещения

При использовании способа вращения иногда происходит наложение изображений. Этого можно избежать, применяя способ плоскопараллельного перемещения.

Сущность этого способа в том, что все точки геометрической фигуры перемещаются в плоскостях параллельных одной из плоскостей проекции.

Следовательно точки движутся в плоскостях уровня, и одна из проекций геометрической фигуры перемещается без изменения формы и размеров, а на другой проекции траектории движения точек параллельны оси x.

Рассмотрим преобразование отрезка АВ прямой общего положения в проецирующую прямую (рис. 5.10). Первоначально преобразуем прямую АВ во франталь, переместив проекцию А₁В₁ без изменения размеров параллельно оси x (в произвольном месте). Точки прямой АВ перемещаются параллельно плоскости p₁. На фронтальной проекции траектории точек параллельны оси x. 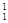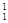Новые фронтальные проекции определяем на пересечений линий связи от А В с траекториями движения точек.

Рис. 5.10. Способ плоскопараллельного перемещения.

Проекция А 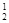В 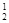является натуральной величиной АВ, т.к. первым перемещение прямая преобразована во фронталь.

Второе перемещение выполним параллельно плоскости p₂. Фронтальную проекцию переместим без изменений размеров перпендикулярно оси x(А 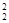В 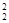^ x). На горизонтальной проекции точки движутся параллельно оси x, и отрезок АВ преобразуется в горизонтально проецирующую прямую.

Задача: Определить расстояние от точки S до плоскости АВС (рис. 5.11) способом плоскопараллельного перемещения.

Решение: Для решения задачи необходимо преобразовать плоскость общего положения в проецирующую. Если одна из проекций плоскости будет преобразована в прямую линию, то можно отпустить перпендикуляр из точки S и определить расстояние. Перемещаем плоскость АВС перпендикулярно плоскости p₂.

Рис. 5.11.

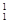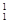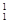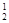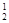Располагаем новую горизонтальную проекцию прямоугольника А В С без изменения формы и размера так, чтобы горизонталь h оказалась перпендикулярно плоскости p₂. На фронтальной проекции точки перемещаются параллельно оси x, Новая фронтальная проекция треугольника А В С 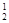преобразуется в прямую линию. Опускаем перпендикуляр из перемещенной точки S на новую фронтальную проекцию треугольника.

Вопросы и задачи для самоконтроля

1. В чём сущность способа перемещения плоскостей проекций?

2. Сколько нужно выполнить последовательных преобразований и каких, чтобы определить натуральную величину плоскости общего положения?

3. Как движутся точки геометрического объекта при его вращении вокруг осей перпендикулярных плоскостям проекции?

4. Сколько нужно выполнить последовательных вращений и каких, чтобы преобразовать прямую общего положения в проецирующую?

5. Определите расстояние между двумя параллельными прямыми общего положения способом плоскопараллельного перемещения?

6. Определите натуральную величину треугольника вращением вокруг фронтали.