Функция потока. Картина поля

Электрическое поле на плоскости можно наглядно представить совокупностью силовых и эквипотенциальных линий – картиной поля.

Под эквипотенциальной поверхностью понимают совокупность точек поля, имеющих один и тот же потенциал.

Если мысленно рассечь электростатическое поле какой--либо секущей плоскостью, то в полученном сечении будут видны следы пересечения плоскости с эквипотенциальными поверхностями. Их называют эквипотенциальными линиями.

Линия силовая электрического поля- линия в пространстве, касательная к которой в каждой точке совпадает по направлению с напряжённостью электрического поля.

Область, заключённая между двумя силовыми линиями, называется

трубкой потока вектора. Поток вектора 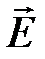внутри силовой трубки постоянен и, равен части заряда провода на единице длины.

Плоскопараллельное поле ― поле картина которого повторяется во всех плоскостях, перпендикулярных какой-либо оси декартовой системы координат (рис.2.3).

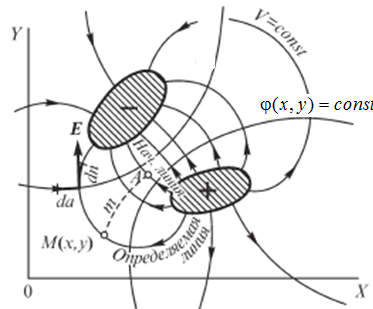
Рис.2.38.Карина поля

Для плоскопараллельного поля уравнение линии равного потенциала:

.

Для описания силовых линий введем понятие функции потока. Одну из силовых линий примем за начальную (нулевую), полагая на ней функцию потока равной нулю (рис.2.38). Соединим произвольную точку M(x,y) c некоторой точкой А начальной линии отрезком MmA. Обозначим через поток вектора сквозь поверхность, которую описал бы отрезок MmA, перемещаясь параллельно самому себе в напралении оси 0z и проходя путь l. Поток на единицу длины обозначим как .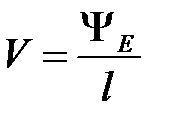

Велчина V, зависит от положения точки M , т.е. является функцией ее координат, что запишем в виде V (x, y). Функцию V (x, y) называют фунуцией потока. Функция V (x, y) имеет постоянное значение на выбранной силовой линии. Поэтому уравнение

V (x, y)=const

является уравнением этой силовой линии.

Функция потока V (x, y) в данной точке равна потоку вектора в трубке, ограниченной силовыми линиями: проходящей через данную точку и начальной силовой линией.

Эквипотенциальные и силовые линии в любой точке поля пересекаются под прямым углом, т. е. образуют в плоскости x0у ортогональную сетку (рис.2.38). Пусть dn ― элемент длины линии напряженности поля и dτ ― элемент длины линии равного потенциала. Координату n будем считать возврастающей в направлении вектора . Координату τ будем считать возврастающей влево от вектора для наблюдателя, расположившегося так, что для него вектор направлен снизу вверх. Примем, что функция V возврастает в том же направлении, в котором увеличивается координата τ. При этих условиях Напряжённость электрического поля выражена через j и V в форме

.

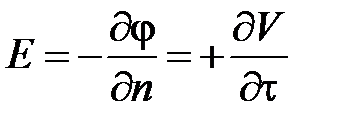Первое соотношение знакомо:

.

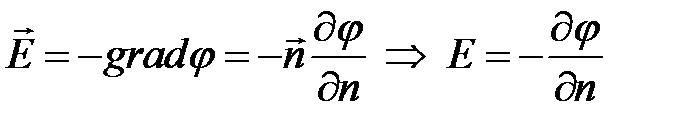Соотношение 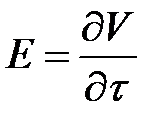следует из тследующего. Давая приращение только координате τ, получим соответствующее приращение потока . Поток проходит через поверхность 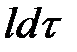. Так как эта поверхность нормальна к линиям напряженности поля, то напряженности поля, то

.

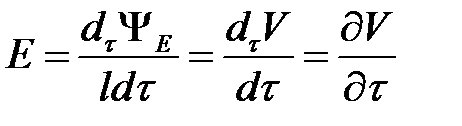2.10. 2.10.Расчёт электростатических полей