Граничные условия для векторов электрического поля
Пусть наповерхности раздела двух диэлектриков с различными диэлектрическими проницаемостями ε1 и ε2 распределен поверхностный заряд плотностью σ.
Окружим точку на поверхности раздела сред элементарнымцилиндром (высота цилиндра 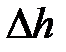 много меньше радиуса) таким образом, чтобы его основания находились в разных средах и были перпендикулярны к нормали, проведенной в рассматриваемой точке (рис.2.2). Этот цилиндр охватывает малую площадку
много меньше радиуса) таким образом, чтобы его основания находились в разных средах и были перпендикулярны к нормали, проведенной в рассматриваемой точке (рис.2.2). Этот цилиндр охватывает малую площадку 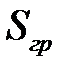 на поверхности раздела сред с зарядом σ
на поверхности раздела сред с зарядом σ 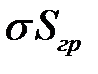 .
.
Векторы электрического смещения в первой и второй средах обозначим соответственно 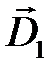 и
и 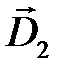 .
.
Применим к поверхности цилиндра теорему Гаусса
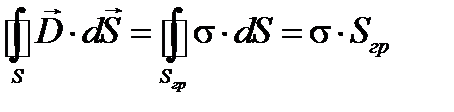 ,
,
где S ― поверхность элементарного цилиндра.
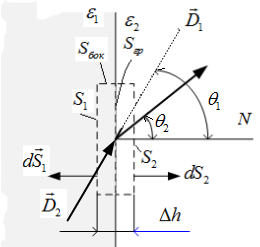
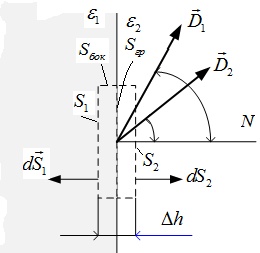
Рис.2.2. Векторы элекрического смещения на границе сред
Устремим объём цилиндра к нулю при условие, что высота цилиндра много меньше его радиуса. В этом случае можно пренебречь потоком вектора сквозь боковую поверхность. Учитывая малые размеры площадок оснований, можно считать что вектор 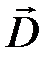 в пределах своей площадки имеет одно и то же значение. С учетом этого после интегрирования для проекций вектора на номаль
в пределах своей площадки имеет одно и то же значение. С учетом этого после интегрирования для проекций вектора на номаль 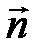 получим
получим
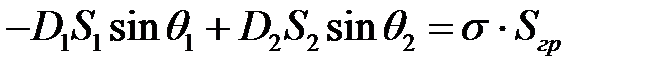 (*)
(*)
или
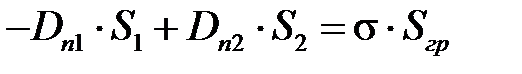 .
.
Учитывая, что 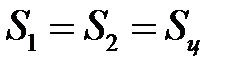 , после сокращения получаем граничное условие нормальной составляющей вектора электрического смещения
, после сокращения получаем граничное условие нормальной составляющей вектора электрического смещения
Dn2–Dn1= σ. (**)
Нормальная проекция вектора электрического смещения на границе раздела двух сред претерпевает скачок, равный поверхностной плотности свободных зарядов, распределенных на этой границе.
При отсутствии на поверхности раздела сред поверхностного заряда имеем 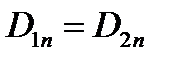 .
.
На границе раздела двух диэлектриков в случае отсутствия на границе раздела двух сред свободного заряда равны нормальные составляющие вектора электрического смещения.
Выделим на границе раздела сред малый контуртаким образом, чтобы его стороны ab и cd находились в разных средах и были перпендикулярны к нормали, проведенной в рассматриваемой точке (рис.2.3). Размеры сторон устремим к нулю контура удовлетворяют условию 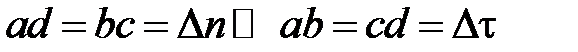 .
.
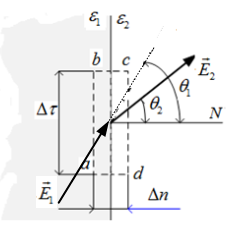
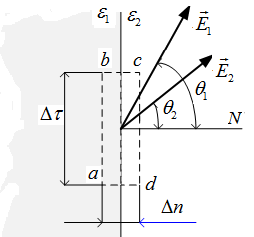
Рис.2.3. Векторы напряженности электрического поля на границе сред
Применим к контуру второе уравнение Максвелла в интегральной форме:
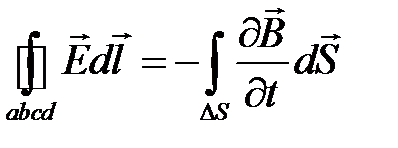 ,
,
где 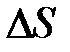 ― площадь поверхности, ограниченной контуром abcd;
― площадь поверхности, ограниченной контуром abcd; 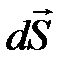 ― вектор элементарной площадки, направленный перпедикулярно к площадке
― вектор элементарной площадки, направленный перпедикулярно к площадке 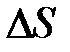 .
.
При интегрировании пренебрегаем вкладом в интеграл на боковых сторонах da и bc ввиду их малости. Тогда:
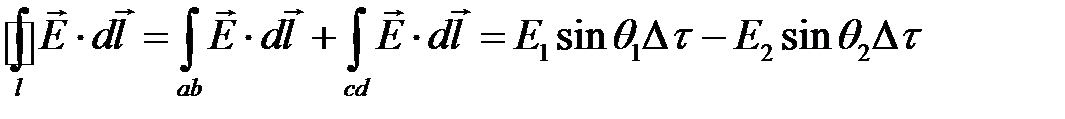 .
.
Так как 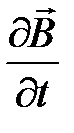 конечная величина, а
конечная величина, а 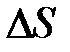 стремится кнулю, то
стремится кнулю, то 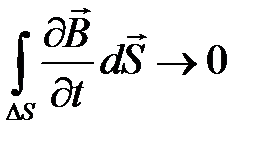
Отсюда
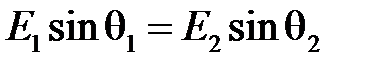 (***)
(***)
или
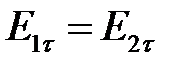 .
.
На границе раздела двух диэлектриков равны тангенциальные составляющие вектора напряженности электрического поля.
При отсутствии на поверхности раздела сред поверхностного заряда из
Выражений (*) и (*** )получаем соотношение, определяющее преломление векторов 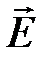 и
и 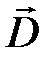 на границе раздела сред
на границе раздела сред
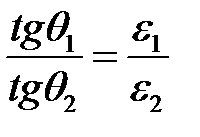 .
.
Для потенциала на границе имеем 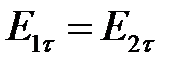 или
или 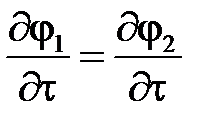 . Интегриуя последнее равенство, получим:
. Интегриуя последнее равенство, получим:
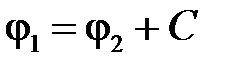 ,
,
где  ― произвольная постоянная.
― произвольная постоянная.
Постоянную  в большинстве случаев можно считать равной нулю. Действительно, потенциал и, созданный объемными или поверхностными зарядами, является непрерывной функцией. При этом имеем:
в большинстве случаев можно считать равной нулю. Действительно, потенциал и, созданный объемными или поверхностными зарядами, является непрерывной функцией. При этом имеем:
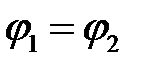 .
.
На поверхности раздела двух диэлектриков с разными электрическими свойствами потенциал непрерывен.
Электростатическое поле внутри проводника (рис. 2.4) отсутствует ( 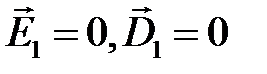 ).
).
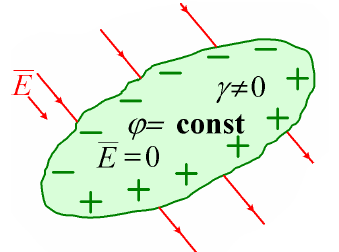

Рис. 2.4. Проводник вэлектрическом поле
Поверхность проводника является поверхностью равного потенциала.
Отсюда касательная (тангенциальная) составляющая вектора E в диэлектрике около поверхности проводника 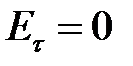 . Тогда линии напряженности и смещения поля в диэлектрике нормальны к проводящей поверхности (рис. 2.5).
. Тогда линии напряженности и смещения поля в диэлектрике нормальны к проводящей поверхности (рис. 2.5).
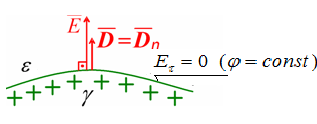
Рис.2.5. Граничное условие на поверхности проводника
На поверхности проводника бесконечно тонким слоем будут располагаться свободные разряды с поверхностной плотностью 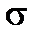 . Плотность свободных зарядов на поверхности проводящего тела равна нормальной составляющей вектора электрической индукции:
. Плотность свободных зарядов на поверхности проводящего тела равна нормальной составляющей вектора электрической индукции:
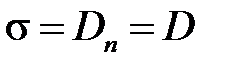 .
.
Дата добавления: 2017-08-01; просмотров: 3675;
