Уравнение Пуассона и Лапласа

Ранее было получено 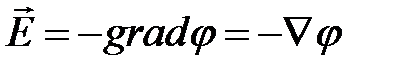. Тогда:

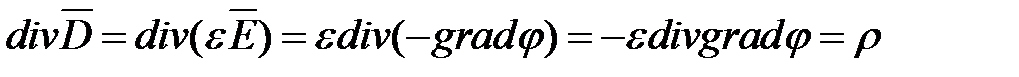, откуда получаем уравнением Пуассона:

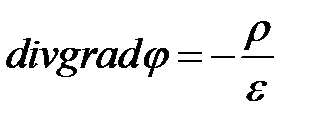или .

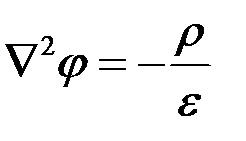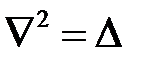- опера́тор Лапла́са (лапласиа́н, оператор дельта).

В декартовой системе координат 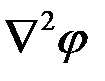может быть представлено в форме

.

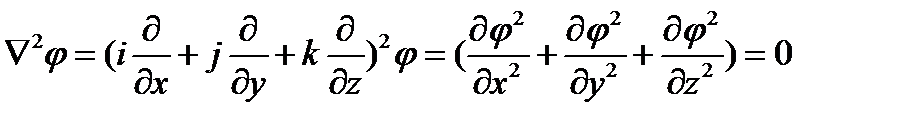Решение уравнения Пуассона в общем виде можно найти следующим образом. Положим, что в объеме V есть заряды плотностью r. Эти заряды представим в виде совокупности точечных зарядов rdV, где dV ― элемент объема. Составляющая потенциала dj электрического поля от элементарного заряда rdV равен .

Значение j определяется как сумма (интеграл) потенциалов от всех зарядов поля:

.

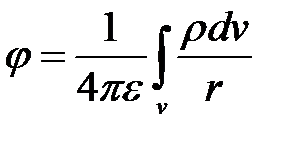Предполагается, что потенциал на бесконечности равен нулю и заряды, создающие поля распределены в ограниченной области (иначе интеграл может оказаться расходящимся).

В реальных условиях свободные заряды располагаются на поверхности проводников бесконечно тонким слоем. В диэлектриках, которыми разделены заряженные проводники, объемные заряды от­сутствуют 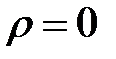. В этом случае в диэлектрике имеем уравнение Лапласа:

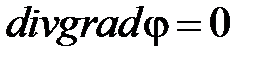или .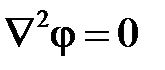

Для однозначного решения дифференциальных уравнений поля необходимы граничные условия.