Гидравлические сопротивления. Уравнение Бернулли для потока несжимаемой жидкости
К одномерным относятся течения, описываемые одной координатой. Для установившихся течений одномерное уравнение Бернулли для потока конечных размеров имеет вид
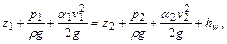 (6.1)
(6.1)
где 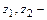 геометрические высоты расположения центров тяжести сечений относительно горизонтальной плоскости сравнения (удельные потенциальные энергии сечений);
геометрические высоты расположения центров тяжести сечений относительно горизонтальной плоскости сравнения (удельные потенциальные энергии сечений); 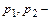 избыточные давления;
избыточные давления; 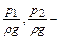 пьезометрические напоры (удельные потенциальные энергии давления);
пьезометрические напоры (удельные потенциальные энергии давления); 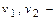 средние скорости в сечениях, определяемые как отношение расхода
средние скорости в сечениях, определяемые как отношение расхода 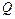 к площади живого сечения S;
к площади живого сечения S; 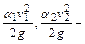 скоростные (динамические) напоры (удельные кинетические энергии);
скоростные (динамические) напоры (удельные кинетические энергии); 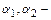 коэффициенты кинетической энергии (коэффициенты неравномерности распределения местных скоростей по живым сечениям потока)
коэффициенты кинетической энергии (коэффициенты неравномерности распределения местных скоростей по живым сечениям потока) 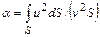 ;
; 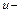 местные скорости течения;
местные скорости течения; 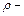 плотность жидкости;
плотность жидкости; 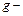 ускорение свободного падения;
ускорение свободного падения; 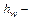 полные потери напора (удельные потери энергии потока) (рис.6.1). Индексы указывают на принадлежность к сечениям потока 1-1 и 2-2 соответственно. Составляющие полной энергии потока называются удельными, поскольку отнесены к единице веса жидкости.
полные потери напора (удельные потери энергии потока) (рис.6.1). Индексы указывают на принадлежность к сечениям потока 1-1 и 2-2 соответственно. Составляющие полной энергии потока называются удельными, поскольку отнесены к единице веса жидкости.
При ламинарном течении в круглых трубах 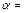 2, при развитом турбулентном
2, при развитом турбулентном 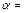 1,1. В общем случае значение
1,1. В общем случае значение 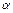 зависит от формы эпюры скорости и может значительно превышать единицу. Компонент уравнения Бернулли
зависит от формы эпюры скорости и может значительно превышать единицу. Компонент уравнения Бернулли 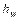 выражает потерю удельной энергии между сечениями 1-1 и 2-2. В гидродинамике приняты следующие обозначения:
выражает потерю удельной энергии между сечениями 1-1 и 2-2. В гидродинамике приняты следующие обозначения: 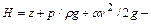 гидродинамический, или полный напор;
гидродинамический, или полный напор; 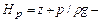 пьезометрический напор;
пьезометрический напор; 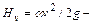 скоростной напор или «скоростная» высота.
скоростной напор или «скоростная» высота.
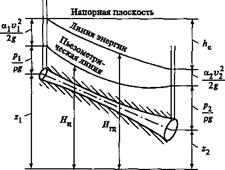
Рис.6.1. Геометрическая интерпретация уравнения Бернулли
для потока несжимаемой жидкости
Основной причиной потерь энергии 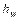 в потоке жидкости являются силы вязкости, которые проявляются в виде потерь механической энергии и складываются из потерь по длине
в потоке жидкости являются силы вязкости, которые проявляются в виде потерь механической энергии и складываются из потерь по длине 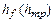 и потерь на местные сопротивления
и потерь на местные сопротивления 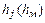 ,
, 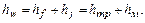
Потери по длине
Потери по длине возникают при течении жидкостей и газов по цилиндрическим трубам или каналам с постоянной по длине потока средней скоростью. В этих случаях потери напора определяются по формуле Дарси - Вейсбаха
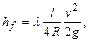 (6.2)
(6.2)
где 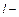 длина потока, на котором возникают потери;
длина потока, на котором возникают потери; 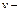 средняя скорость; R - гидравлический радиус, определяемый как отношение площади нормального сечения потока к смоченному периметру
средняя скорость; R - гидравлический радиус, определяемый как отношение площади нормального сечения потока к смоченному периметру 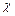 ,
, 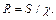
Для круглых труб 4R = d , где d - диаметр трубы и формула приобретает вид
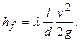 (6.3)
(6.3)
Потери энергии, выраженные в размерности давления, определяются по формуле
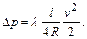 (6.4)
(6.4)
Гидравлический коэффициент трения 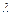 в общем случае зависит от геометрических и физических условий на границах потока (формы поперечного сечения и шероховатости стенок) и числа Рейнольдса Re. Общий характер зависимости
в общем случае зависит от геометрических и физических условий на границах потока (формы поперечного сечения и шероховатости стенок) и числа Рейнольдса Re. Общий характер зависимости 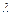 от числа Re и шероховатости стенок для круглых труб по данным опытов Никурадзе показан на рис.6.1. В этих опытах шероховатость создавалась искусственно и оценивалась средним размером выступа
от числа Re и шероховатости стенок для круглых труб по данным опытов Никурадзе показан на рис.6.1. В этих опытах шероховатость создавалась искусственно и оценивалась средним размером выступа 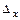 . Различаются следующие режимы течения: 1 - ламинарный; 2 - гладкостенный турбулентный; 3 – доквадратичный турбулентный; 4 - квадратичный турбулентный.
. Различаются следующие режимы течения: 1 - ламинарный; 2 - гладкостенный турбулентный; 3 – доквадратичный турбулентный; 4 - квадратичный турбулентный.
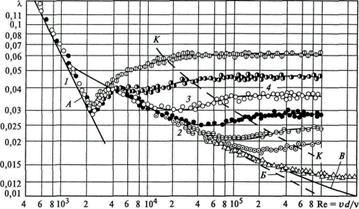
Рис.6.2. Зависимость гидравлического коэффициента трения от числа Рейнольдса
для круглых труб с однородной шероховатостью:
1-2 - зоны ламинарного и гладкостенного режимов; 3-4 - зоны доквадратичного и квадратичного сопротивлений; К-К - нижняя граница квадратичного режима; А - расчет по формуле 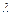 = 64 /Re; Б - расчет по формуле
= 64 /Re; Б - расчет по формуле 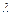 = 0,316/Re0,25; В - расчет по формуле Прандтля
= 0,316/Re0,25; В - расчет по формуле Прандтля 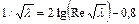 .
.
Таблица 6.1
Эквивалентная абсолютная шероховатость труб из разных материалов
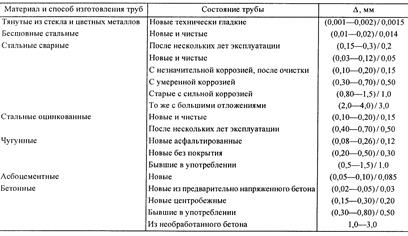
Примечание. В числителе приведены пределы изменения 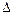 , в знаменателе - его средние значения.
, в знаменателе - его средние значения.
Для промышленных труб, в которых шероховатость неравномерна, в качестве ее характеристики применяется эквивалентная абсолютная шероховатость 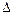 , значения которой приведены в табл.6.1. Графическая зависимость
, значения которой приведены в табл.6.1. Графическая зависимость 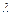 от
от 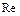 для таких труб приведена на рис.6.3.
для таких труб приведена на рис.6.3.
Наиболее распространенные зависимости для коэффициента 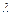 даны в табл.6.1.
даны в табл.6.1.
Сжимаемость газов мало влияет на зависимость 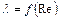 , о чем свидетельствуют опытные данные, приведенные на рис.6.5. Однако в области чисел Маха М, близких к 1, наблюдаются заметные отклонения значений
, о чем свидетельствуют опытные данные, приведенные на рис.6.5. Однако в области чисел Маха М, близких к 1, наблюдаются заметные отклонения значений 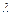 для газа от значений этого коэффициента для несжимаемой жидкости (рис.6.6).
для газа от значений этого коэффициента для несжимаемой жидкости (рис.6.6).
Внутренняя структура течения в круглых трубах зависит от режимов течения.
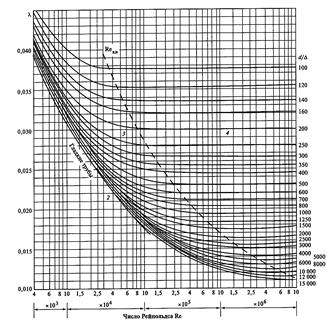
Рис.6.3. Расчетный график гидравлического коэффициента трения
для стальных круглых труб с естественной шероховатостью, по данным ВТИ:
2-4 - зоны соответственно гладкостенного, доквадратичного и квадратичного режима;
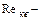 нижнее граничное число Рейнольдса квадратичной зоны сопротивления
нижнее граничное число Рейнольдса квадратичной зоны сопротивления
При стабилизированном ламинарном течении распределение местных скоростей подчиняется параболическому закону
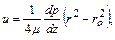 (6.5)
(6.5)
или в безразмерном виде
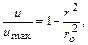 (6.6)
(6.6)
где р - давление; 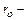 радиус трубы;
радиус трубы; 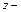 координата, отсчитываемая вдоль оси трубы вниз по течению;
координата, отсчитываемая вдоль оси трубы вниз по течению; 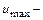 максимальная скорость.
максимальная скорость.
Таблица 6.2
Расчетные формулы для гидравлического коэффициента трения

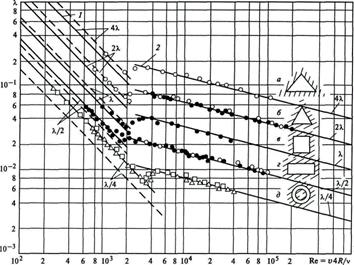
Рис.6.4. Зависимость гидравлического коэффициента трения
от числа Рейнольдса для труб некруглого сечения:
1 - ламинарное течение, 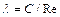 ; 2 - турбулентное течение
; 2 - турбулентное течение 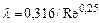 ;
;
_ _ - ламинарное течение в круглой трубе, 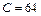 ; а - равнобедренный прямоугольный треугольник,
; а - равнобедренный прямоугольный треугольник, 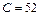 ; б - равносторонний треугольник,
; б - равносторонний треугольник, 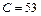 ; в - квадрат,
; в - квадрат, 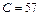 ; г - прямоугольник (
; г - прямоугольник ( 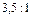 ),
), 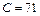 ; д - кольцевая щель,
; д - кольцевая щель, 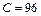 ;
;  - измерения Никурадзе;
- измерения Никурадзе;  - измерения Шиллера;
- измерения Шиллера;  -
- 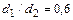 ; -
; - 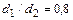 , измерения Коха и Файнда
, измерения Коха и Файнда
Средняя скорость в 2 раза меньше максимальной: 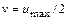 . Падение давления
. Падение давления 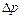 на участке горизонтальной трубы длиной
на участке горизонтальной трубы длиной 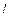 определяют по формуле Пуазейля
определяют по формуле Пуазейля
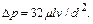 (6.7)
(6.7)
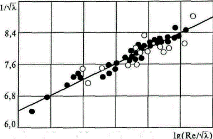
Рис.6.5. Зависимость гидравлического коэффициента трения
для гладкой трубы от числа Рейнольдса:
 - дозвуковое течение;
- дозвуковое течение;  - сверхзвуковое течение;
- сверхзвуковое течение;
расчет по формуле Прандтля – Никурадзе 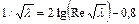
Из уравнения Бернулли, составленного для граничных сечений участка 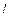 , следует, что
, следует, что 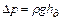 , где
, где 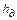 - потери напора и, следовательно,
- потери напора и, следовательно,
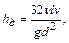 (6.8)
(6.8)
откуда вытекает, что 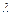 = 64 /Re, где Re =
= 64 /Re, где Re = 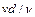 . Для наклонной трубы падение гидродинамического напора:
. Для наклонной трубы падение гидродинамического напора:
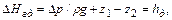 (6.9)
(6.9)
где 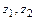 - отметки центров тяжести сечений трубы в начале и конце участка
- отметки центров тяжести сечений трубы в начале и конце участка 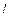 .
.
Стабилизированное течение устанавливается лишь на некотором расстоянии от входа в трубу, за пределами начального участка, длина которого для круглой трубы 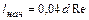 .
.
Падение давления на начальном участке не подчиняется формуле Пуазейля, но приближенно может быть определено по формуле
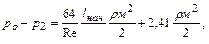 (6.10)
(6.10)
где 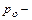 давление в резервуаре, к которому присоединена труба;
давление в резервуаре, к которому присоединена труба; 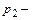 давление в конце начального участка.
давление в конце начального участка.
Разрушение ламинарного режима в трубе и переход к турбулентному режиму происходит при достижении критического числа Рейнольдса. Для круглых труб это значение составляет приблизительно 2300. При 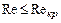 наблюдается устойчивый ламинарный режим; при
наблюдается устойчивый ламинарный режим; при 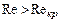 возможно появление турбулентности, но не исключено и сохранение ламинарного режима, который является неустойчивым. Для труб некруглого сечения критическое число Рейнольдса приблизительно равно 2000, причем
возможно появление турбулентности, но не исключено и сохранение ламинарного режима, который является неустойчивым. Для труб некруглого сечения критическое число Рейнольдса приблизительно равно 2000, причем 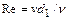 , где
, где 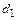 - гидравлический диаметр, определяемый соотношением
- гидравлический диаметр, определяемый соотношением 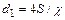 , в котором - смоченный периметр сечения
, в котором - смоченный периметр сечения 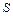 трубы.
трубы.
При стабилизированном турбулентном течении в трубах распределение местных осредненных скоростей описывается полуэмпирическими или эмпирическими формулами. Наиболее известные из них:
логарифмическая формула для гладкостенного режима течения
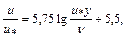 (6.11)
(6.11)
где 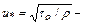 динамическая скорость;
динамическая скорость;
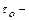 касательное напряжение на стенке;
касательное напряжение на стенке;
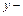 расстояние от стенки.
расстояние от стенки.
Другая форма этой зависимости имеет вид
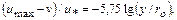 (6.12)
(6.12)
где 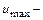 - максимальная скорость (на оси трубы).
- максимальная скорость (на оси трубы).
Средняя скорость связана с максимальной соотношением
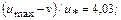 (6.13)
(6.13)
универсальная логарифмическая формула для всех турбулентных режимов в шероховатых трубах
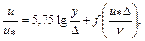 (6.14)
(6.14)
где функция 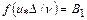 определяется графиком, приведенном на рис. 6.7;
определяется графиком, приведенном на рис. 6.7;
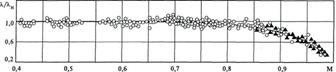
Рис.6.6. Влияние числа Маха на гидравлический коэффициент трения
при дозвуковом течении газа в гладкой трубе:
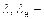 коэффициенты трения для газа и несжимаемой жидкости;
коэффициенты трения для газа и несжимаемой жидкости;
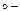 опыты МЭИ;
опыты МЭИ;  опыты МО ЦКТИ
опыты МО ЦКТИ
степенная формула (эмпирическая)
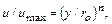 (6.15)
(6.15)
где показатель 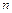 в зависимости от числа Re изменяется от 1/6 до 1/10. Значение, соответствующее гладкостенному режиму (при
в зависимости от числа Re изменяется от 1/6 до 1/10. Значение, соответствующее гладкостенному режиму (при 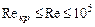 ):
): 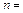 1/7.
1/7.
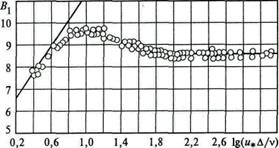
Рис.6.7. Вид функции 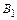 определяющей закон распределения скоростей
определяющей закон распределения скоростей
в шероховатых трубах
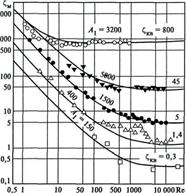
Рис. 6.8. Зависимость коэффициента местных сопротивлений от числа Рейнольдса:
- тройник; Ñ - шаровой клапан;  - угольник 90°;
- угольник 90°;  - разъемный клапан;
- разъемный клапан;
 - диафрагма (при отношении площади отверстия к площади трубы
- диафрагма (при отношении площади отверстия к площади трубы 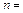 0,05)
0,05)
Дата добавления: 2018-06-28; просмотров: 1228;
