Поле двух параллельных разноименно заряженных осей

Две разно­именно заряженные оси 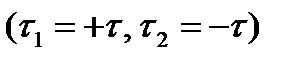расположены параллельно на расстоянии 2b в ди­электрическом пространстве (рис.2.713).

Вектор напряженности поля равен геометрической сумме векторов, а результирующий потенциал ― ал­гебраической сумме потенциалов от каж­дого провода:

.

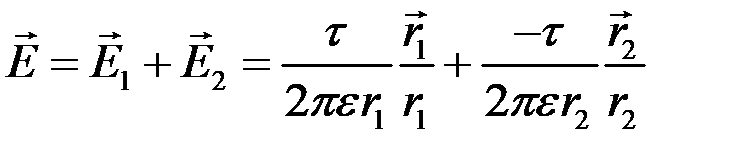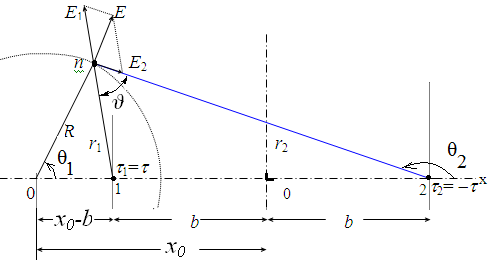
Рис.2.713. К определению поля двух линейных зарядов

Результирующий вектор напряженности поля равен геометрической сумме составляющих, а результирующий потенциал – ал­гебраической сумме составляющих от каж­дого провода:

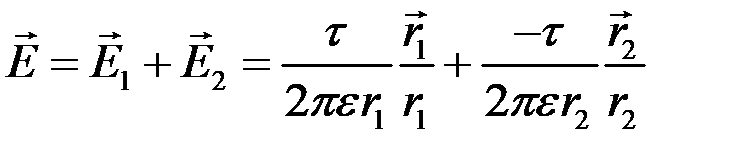Потенциал равен ал­гебраической сумме потенциалов от каж­дого провода:

.

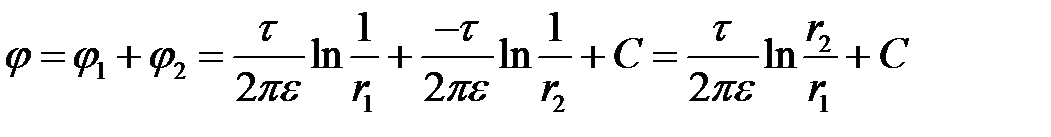Если принять 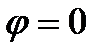в точках равноудалённых от обеих осей ( 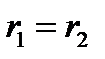), то постоянная интегрирования будет равна нулю (С=0).

Тогда получим: .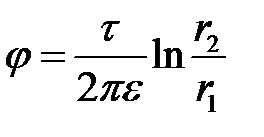

Эквипотенциальные поверхности удовлетворяют условию

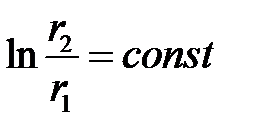или .

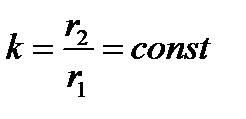
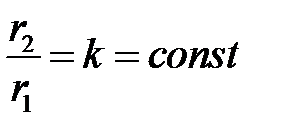Гео­метрическим местом точек, отношение расстояний от которых до заданной пары точек по­стоянно, является окружность, центр которой лежит на линии, соединяющей заданную пару точек (т. Аполлония).

Действительно:

; .

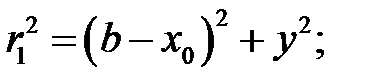
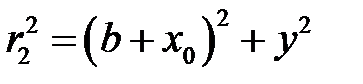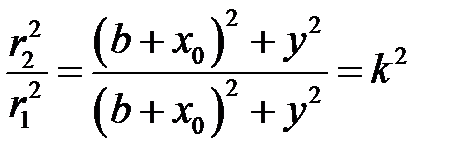После преобразований получаем уравнение окружности:

.

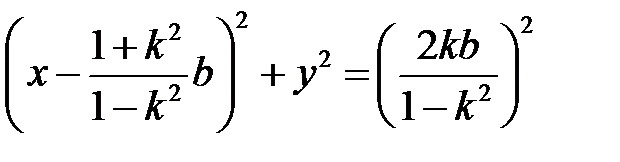Координаты центра окружности равны: 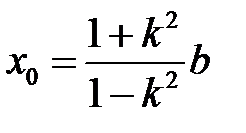, y₀=0.

Радиус окружности:э .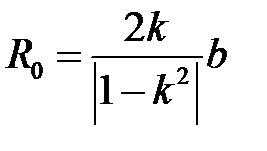

Отсюда для любой линии равного потенциала .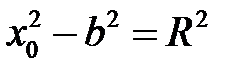

Функция потока V определяется методом наложения с использованием

выражения (2.84):

,

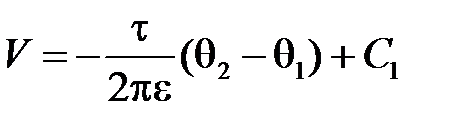где С₁= 0, если считать V = 0 при .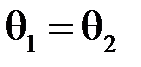

Уравнение любой силовой линии имеет вид:

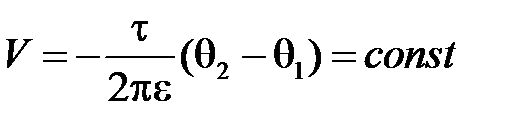или .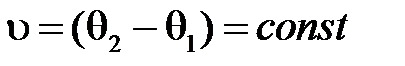

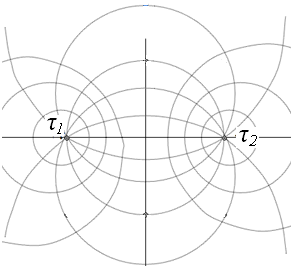
Семейство силовых линий поля образуют дуги окружностей , проходящих через заряженные оси, а центры окружностей расположены на оси симметрии (рис.2.814).

Уравнением дуги окружности является υ=const .

Координаты центра окружности: x₀=0; ;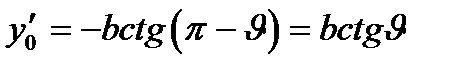

Радиус окружности: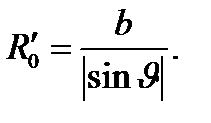

Чтобы подразделить поле на трубки равного потока, следует считать

разность 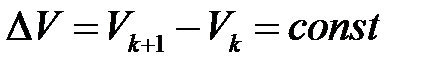одинаковой для двух соседних линий. Для этого необходимо изменять угол ϑ на постоянную величину Δϑ = const. Картина поля приведена на рис.2.814.

Рис.2.814. Поле двух заряженных осей