Пример № 1. Расчет числа параллельных опытов

Задача:необходимо определить число параллельных опытов

Nо для получения достоверных результатов эксперимента по оценке

качества боковой эвольвентной исполнительной поверхности зуба

цилиндрического зубчатого колеса на операции размерной электроэрозионной обработки, реализуемой на станке с ЧПУ.

Решение задачи:

Условия проведения эксперимента:

1) Станок – СВЭИ-7 с генератором импульсов

ГКИ-300-200А;

2) инструмент – проволока диаметром dи = 0,192 мм из ла-

туни Л63, ГОСТ 1066;

3) заготовка – пластина из стали 20Х, ГОСТ 1577;

4) рабочая жидкость – вода, ГОСТ Р 51232;

5) элементы режима обработки: частота следования импульсов f = 44 кГц; сила тока короткого замыкания Iкз = 0,8 А; средняя

сила тока − Iср = 0,6 А; напряжение холостого хода Uо = 150 В; напряжение пробоя между электродом-заготовкой и электродом-инструментом Uпр = 75 В; длительность импульсов τи = 2,5 мкс; период повторения импульсов τпр = 22,7 мкс ; скважность импульсов q= 9 ; сила натяжения проволочного электрода-инструмента F = 8,8 Н; скорость проволочного электрода-инструментаVпр = 28 мм/с; расстояние между верхней и нижней направляющими

проволочного электрода-инструмента ℓпр = 29 мм ; положение заготовки относительно направляющих симметричное;

6) ожидаемая степень точности зубчатого колеса по нормам

плавности работы – восьмая;

7) ожидаемое значение среднего арифметического отклонения профиля – R_a = 1,25 … 1,6 мкм.

Результаты проведения эксперимента.

1) Измерения осуществлялись с помощью профилометра-профилографа Perthometer S5P;

2) результаты измерений сведены в таблицу:

Результаты обработки экспериментальных данных для расчета

числа параллельных опытов:

1) среднее арифметическое значение измеряемой величины:

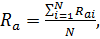(3)

где N число опытов (N = 7).

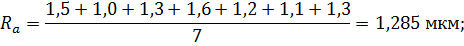
2) величина дисперсии:

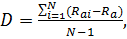(4)

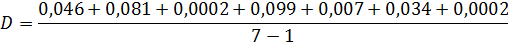
= 0,045 мкм;

3) точность величины математического ожидания:

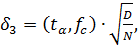(5)

где (t_α , f_c) – квантиль распределения Стьюдента, зависящий от доверительной вероятности γ, уровня значимости α и числа степеней свободы f_c; при γ = 0,95, α = 0,05, f_c = N − 1 = 7 − 1 = 6 значение

(t_α , f_c) = 2,447;

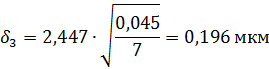
4) доверительные границы значений параметра R_a при уровне значимости α = 0,05:

Ra_{max, min}= Ra ± δ₃ ; (6)

Ra_max = 1,285 + 0,196 = 1,481 мкм;

Ra _min = 1,285 − 0,196 = 1,089 мкм,

таким образом, доверительным является результат, который попадает

в диапазон

1,089 ≤ Ra_i ≤ 1,481 мкм;

5) необходимое число параллельных опытов при проведении экспериментальных исследований:

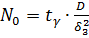, (7)

где tγ– корень уравнения нормированной функции Лапласа Фo (t):

приγ = 0,95, tγ = 1,96;

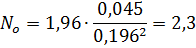
Следовательно, принимаем число параллельных опытов Nо равным трем.

В данном примере реализована методика расчета числа параллельных опытов, которую можно использовать для решения других аналогичных задач.