Пример № 4. Проведение однофакторного технологического эксперимента

Задача:реализовать однофакторный технологический эксперимент для оценки величины силы F_р, воздействующей на крепежный болт из стали 45, которую может выдержать болт, если внутренний диаметр его резьбы d₁ = 3 мм:

(27)

где 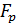− сила растяжения болта, Н; 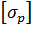– допустимые напряжения

при растяжении, Н/мм²:

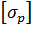= 7,2 Н/мм².

Решение задачи:

Можно реализовать два подхода к нахождению искомого значе-

ния Fр . Определим Fр прямым (точно) и численным (приближенно)

методами.

Выразив Fр из зависимости (27):

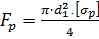(28)

При известных 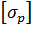= 72 Н/мм² и d₁ = 3 мм:

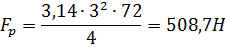
Реализация прямого метода, как правило, оправдывает себя в

случаях, когда нелинейная зависимость является сравнительно простой и не содержит в себе каких-либо показательных, логарифмических, стандартных и нестандартных тригонометрических функций.

В противном случае целесообразно перейти к реализации численных

методов решения нелинейных зависимостей. Одним из таких методов

является метод деления отрезка пополам.

В качестве примера, решим поставленную задачу этим методом.

Построим график зависимости d₁ ( Fр) и определим диапазон Fр, в котором находится искомое решение (рис. 3).

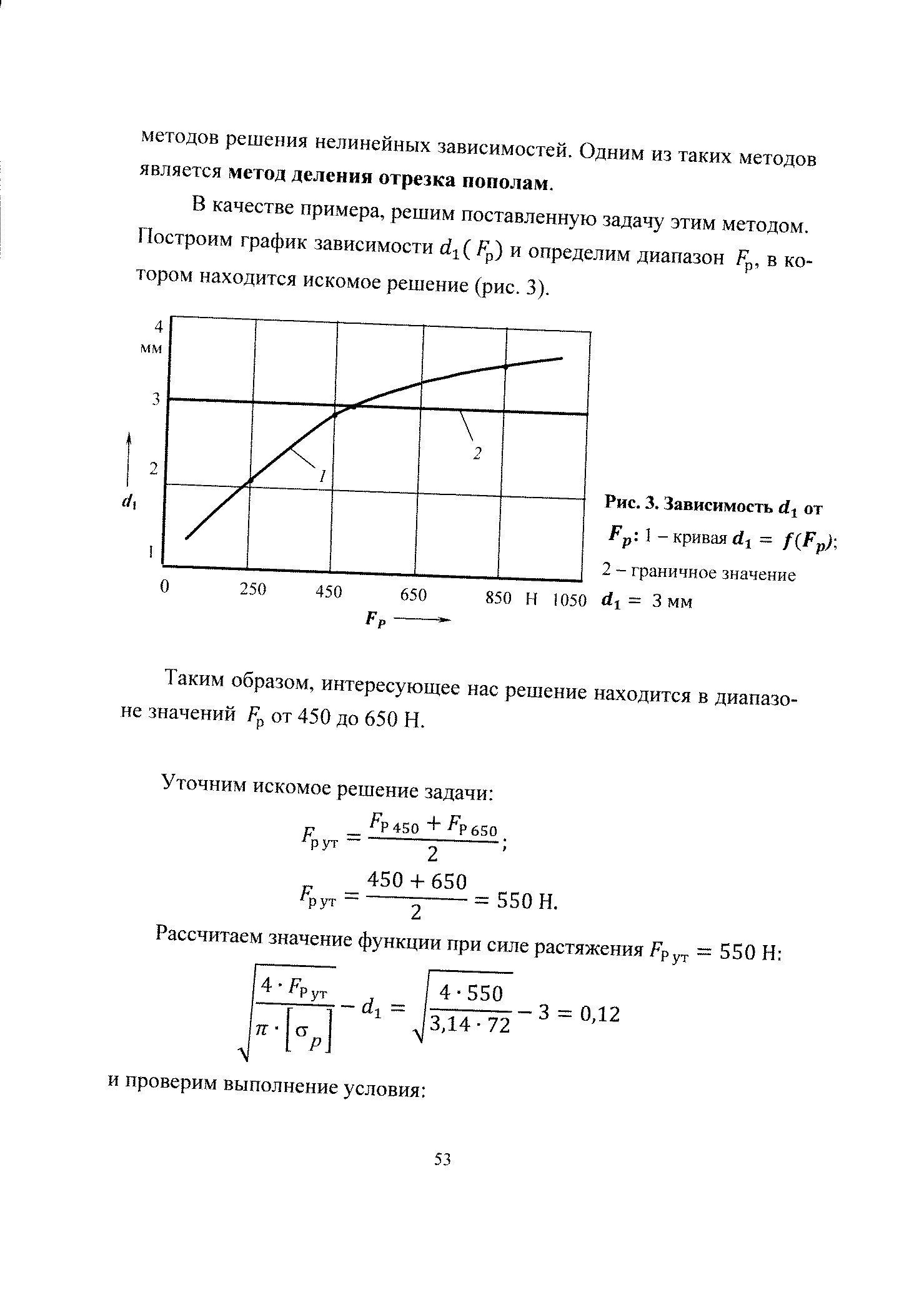
Таким образом, интересующее нас решение находится в диапазоне значений Fр от 450 до 650 Н.

Уточним искомое решение задачи:

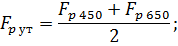
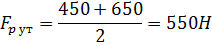
Рассчитаем значение функции при силе растяжения 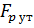= 550 Н:

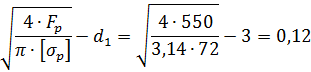
и проверим выполнение условия:

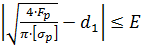, (29)

где Е −точность получения результата решения задачи: Е = 0,1. Поскольку 0,12 ≤ 0,1, условие (29) не выполнено.

Найдем новое уточнение решения задачи:

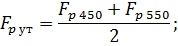
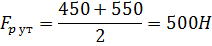
Рассчитаем значение функции при силе растяжения

= 500 Н:

и проверим вновь выполнение условия:

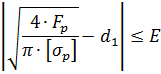
Условие 0,03 ≤ 0,1 выполнено.

Следовательно, величина внешней силы F_p , воздействующей на

крепежный болт диаметром d₁ = 3 мм, не должна превышать 500 Н.

Погрешность численного метода составила 1,7 %. Эту погрешность

можно уменьшить, если ужесточить требования к параметру E

(E → 0).

Подход к решению этой задачи можно перенести и на решение

других аналогичных задач, когда необходимо определить допустимый максимум целевой функции при известном ограничении.

В нашем случае найдено максимальное F_p при заданном ограничении

d₁ = 3 мм.