Пример № 3. Проверка адекватности теоретической зависимости
Задача:проверить адекватностьзависимости | fpbr max| , предназначенной для определения отклонения шага зацепления зубчатого колеса при электроэрозионном зубовырезании.
| fpbr max| = −2,483 + 9,944 · m + 4,509 · 10-2 · z +
+3,780 · 10-2 ∙ N1 – 3,947 · 10-2 · m · z – 0,324 · m · N1 −
−3,095 · 10-4 · z · N1 + 1,850 · 10-3 · z · m · N1
Зависимость должна давать достоверный результат оценки
выходного параметра | fpbr max | для следующих условий:
- станок с ЧПУ СВЭИ-7 (погрешности линейных перемещений
по осям Х и Y одинаковы: Δ 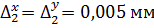 ; дискретность системы
; дискретность системы
ЧПУ – Д = 0,001 мм);
- модуль зубчатого колеса m = 1,25 … 10,00 мм;
- число зубьев зубчатого колеса z = 20 … 80;
- число формообразующих точек N1 = 7 … 30;
- интерполятор системы ЧПУ линейный;
- координаты формообразующих точек траектории задаются в абсолютных величинах;
- распределение формообразующих точек траектории равноудаленное (шаг от точки к точке nℓ =const).
Решение задачи:
Для проверки адекватности предложенной зависимости (2) про-
веден натурный однофакторный эксперимент при следующих условиях:
1) станок – СВЭИ-7 с генератором импульсов ГКИ-300-200 А;
2) инструмент− калиброванная проволока dи = 0,2 мм из латуни
Л63, ГОСТ 1066;
3) заготовка – пластина из стали 20Х, ГОСТ 1577;
4) рабочая жидкость− вода, ГОСТ Р 51232;
5) элементы режима обработки для условий обеспечения восьмой
степени точности зубчатого колеса (Ra = 1,25 мкм – нормируемый
параметр шероховатости боковой эвольвентной поверхности зуба
зубчатого колеса ): частота следования импульсов f = 44 кГц; сила
тока короткого замыкания Jкз = 0,8 А; средняя сила тока Jср = 0,6 А;
напряжение холостого хода Uо = 150 В; напряжение пробоя
Uпр = 75 В; длительность импульсов τи = 2,5 мкс; период повторения
импульсов τпр = 22,7 мкс; скважность импульсов q= 9; сила натяжения проволочного электрода-инструмента F = 8,8 Н; скорость перемотки проволочного электрода-инструмента Uпр = 28 мм/с ; рас-
стояние между направляющими проволочного электрода-инструмента
ℓпр = 29 мм ; положение заготовки относительно направляющих
проволочного электрода-инструмента симметричное;
6) осуществлялась обработка четырех зубчатых колес с m = 1,5; 2,0; 2,5; 3,0 мм при z = 20. Необходимое для обеспечения заданной степени точности число точек N1 = 11; 13; 14; 16 соответственно для m = 1,5; 2,0; 2,5; 3,0 мм;
7) в качестве средства измерения для оценки действительных значений отклонения шага зацепления использовали прибор – УЗП-400 завода МИЗ (универсальный зубоизмерительный прибор), оснащенный индикатором многооборотным 1 МИГ, ГОСТ 9696 с погрешностью измерения ±1 мкм и набором плоскопараллельных концевых мер № 1 и № 2, ГОСТ 9038. Предварительная метрологическая оценка этого прибора показала, что относительная погрешность измерения составляет ±22 %, что меньше допустимой ±30 %;
8) число параллельных опытов Nо принято равным трем (см. пример № 1).
Исходные данные для дисперсионного анализа представлены в табл. 4.
Таблица 4 – Исходные данные для дисперсионного анализа
| Группа | № опыта | m, мкм | z | N1 | | fpbr max|эi , мкм | | fpbr max| рi , мкм |
| 1,5 | 9,0 | 7,8 | ||||
| 1,5 | 7,0 | 7,8 | ||||
| 1,5 | 8,5 | 7,8 | ||||
| 2,0 | 9,0 | 9,7 | ||||
| 2,0 | 12,0 | 9,7 | ||||
| 2,0 | 10,0 | 9,7 | ||||
| 2,5 | 14,0 | 12,5 | ||||
| 2,5 | 12,5 | 12,5 | ||||
| 2,5 | 15,0 | 12,5 | ||||
| 3,0 | 17,0 | 14,6 | ||||
| 3,0 | 14,5 | 14,6 | ||||
| 3,0 | 15,0 | 14,6 |
Примечание. Индекс э− натурный эксперимент; индекс р − расчет по теоретической зависимости.
Проверим наличие промаховв каждой из четырех групп
результатов измерения | fpbr max|эi, мкм, по критерию Шовине, учитывая, что число параллельных опытов (Nо = 3).
Результат измерения является промахом, если

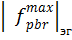 – среднее арифметическое значение результатов измерения в группе, мкм;
– среднее арифметическое значение результатов измерения в группе, мкм;
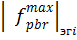 – результат измерения в группе, мкм;
– результат измерения в группе, мкм;
σ –средняя квадратическая погрешность единичного измерения:
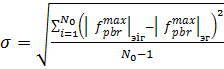 (13)
(13)
Результаты обработки данных сведены в табл. 5, из которой следует, что во всех группах промахов нет.
Таблица 5 – Результаты оценки наличия промахов
| Группа | 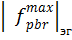 , мкм , мкм
| 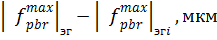
| 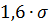
|
| 8,17 | 0,83 | 1,66 | |
| 1,17 | |||
| 0,33 | |||
| 10,33 | 1,33 | 2,45 | |
| 1,67 | |||
| 0,33 | |||
| 13,83 | 0,17 | 2,016 | |
| 1,33 | |||
| 1,17 | |||
| 15,5 | 1,50 | 2,13 | |
| 1,00 | |||
| 0,50 |
Таким образом, результаты измерения 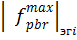 являются достоверными, и их можно использовать для последующего дисперсионного анализа.
являются достоверными, и их можно использовать для последующего дисперсионного анализа.
Среднее арифметическое всех экспериментальных данных:
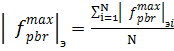 (14)
(14)
где N – суммарное число опытов: N = 12;
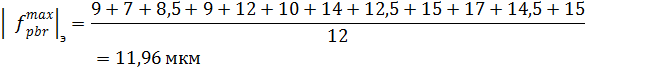
Определим сумму остатков:
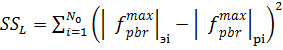 (15)
(15)
 = 1,44 + 0,64 + 0,49 + 0,49 + 5,29 + 0,09 + 2,25 + 0 + 6,25 +
= 1,44 + 0,64 + 0,49 + 0,49 + 5,29 + 0,09 + 2,25 + 0 + 6,25 +
+5,76 + 0,01 + 0,16 = 22,87мкм.
Сумма регрессии:
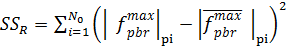 (16)
(16)
 = 17,31 + 17,31 + 17,31 + 5,11 + 5,11 + 5,11 + 0,29 + 0,29 +
= 17,31 + 17,31 + 17,31 + 5,11 + 5,11 + 5,11 + 0,29 + 0,29 +
+0,29 + 6,97 + 6,97 + 6,97 = 89,04 мкм.
Сумма квадратов «чистой» ошибки:
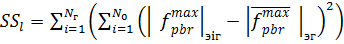 (17)
(17)
где Nг − число групп опытов: Nг = 4; N0 = 3;
 = 2,18 + 4,67 + 3,17 + 3,50 = 13,52 мкм2.
= 2,18 + 4,67 + 3,17 + 3,50 = 13,52 мкм2.
Средний квадрат регрессии:
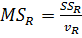 (18)
(18)
где 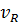 − число степеней свободы регрессии:
− число степеней свободы регрессии: 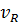 = 1 (однофакторный
= 1 (однофакторный
эксперимент), следовательно 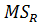 = 89,04 мкм.
= 89,04 мкм.
Средний квадрат остатка:
 (19)
(19)
где 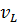 −число степеней свободы остатка:
−число степеней свободы остатка: 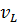 =
= 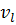 +
+ 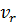 ,
,
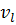 − число степеней свободы «чистой» ошибки:
− число степеней свободы «чистой» ошибки:
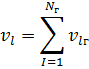
где 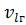 − число степеней свободы группы (см. табл. 4):
− число степеней свободы группы (см. табл. 4):
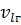 = Nо − 1;
= Nо − 1; 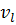 = 2 + 2 + 2 + 2 = 8 ;
= 2 + 2 + 2 + 2 = 8 ;
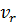 − число степени свободы неадекватности:
− число степени свободы неадекватности:
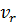 = Nо − 1;
= Nо − 1; 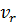 = 3 − 1 = 2.
= 3 − 1 = 2.
Следовательно,
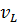 = 8 + 2 = 10.
= 8 + 2 = 10.
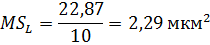
Средний квадрат «чистой» ошибки:
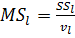 (20)
(20)
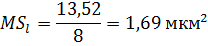
Средний квадрат неадекватности:
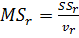 (21)
(21)
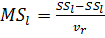 (22)
(22)
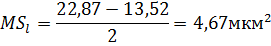
Сумма квадратов скорректированного источника дисперсии
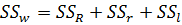 ; (23)
; (23)
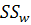 = 89,04 + 9,35 + 13,52 = 111,91 мкм2.
= 89,04 + 9,35 + 13,52 = 111,91 мкм2.
Расчетный критерий Фишера:
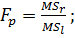 (24)
(24)
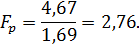
Табличный критерий Фишера:
FT = 4,46,
так как vr = 2, vl = 8, γ = 0,95 (95 %).
Так как Fp < FT, то зависимость для определения отклонения
шага зацепления | fpbr max |, мкм, адекватно описывает взаимосвязь этого
выходного параметра с входными конструктивно-технологическими
параметрами.
Дополнительно определим величину коэффициента детерминации и множественного коэффициента корреляции:
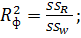 (25)
(25)
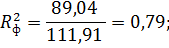
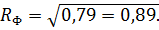
Так как RФ> 0,51, то существует тесная корреляционная связь
между экспериментальными и расчетными значениями отклонения
шага зацепления зубчатого колеса.
Исходная зависимость | fpbr max |, позволяет на 89 % объяснить общий
разброс данных относительно среднего 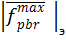 .
.
Оценим степень соответствия этой зависимости результатам экспериментальных данных путем построения графиков (рис. 2).
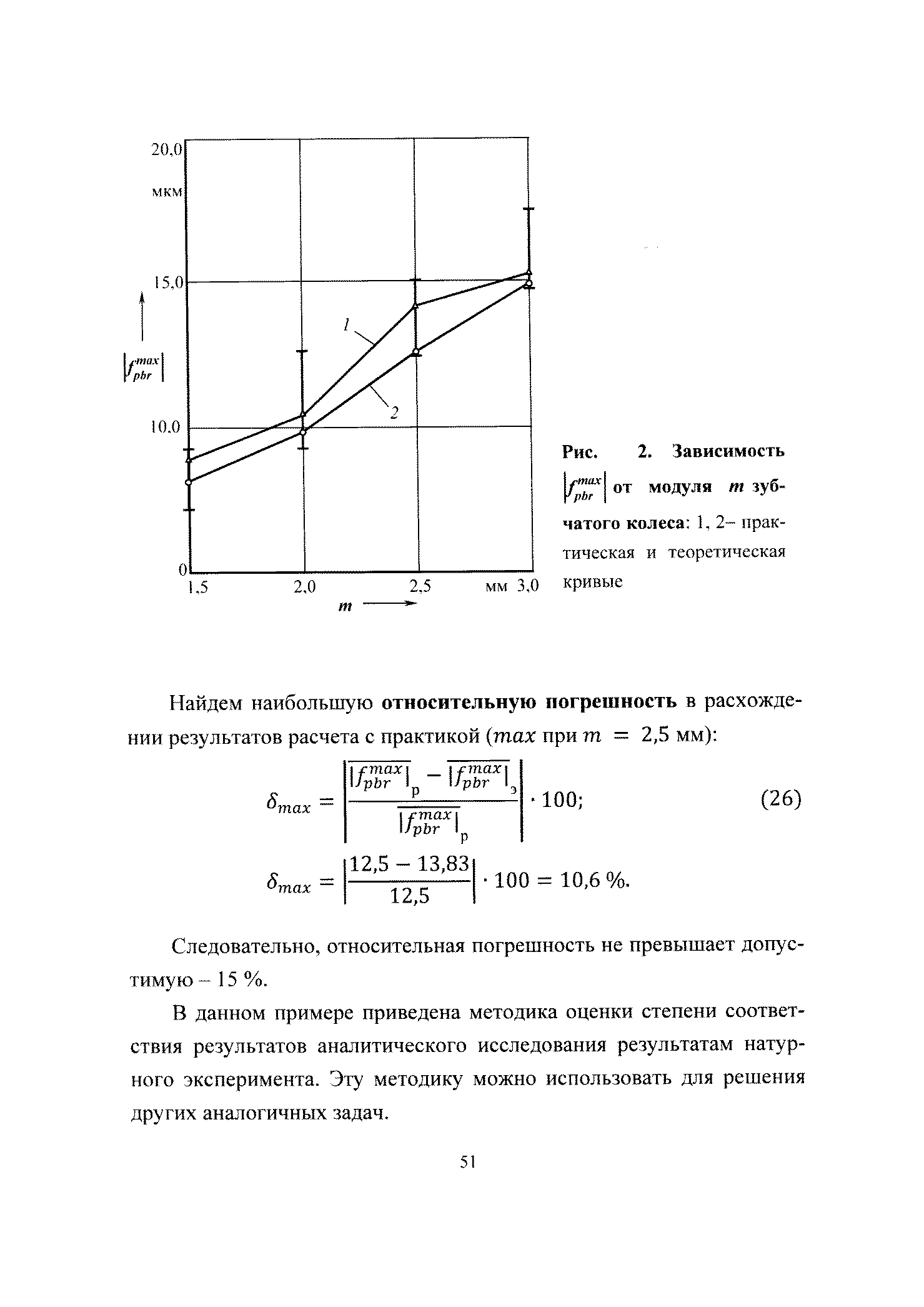
Найдем наибольшую относительную погрешностьв расхождении результатов расчета с практикой (max при m = 2,5 мм):
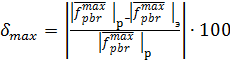 (26)
(26)
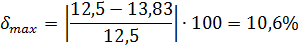
Следовательно, относительная погрешность не превышает допустимую – 15 %.
В данном примере приведена методика оценки степени соответствия результатов аналитического исследования результатам натурного эксперимента. Эту методику можно использовать для решения других аналогичных задач.
Дата добавления: 2017-02-20; просмотров: 697;
