Пример № 6. Поиск оптимального значения целевой функции

Задача: определить условия обеспечения минимального значения параметра Rz, мкм, при обработке отверстия сверлением по экспериментальной зависимости:

(32)

где Rz − высота неровностей профиля по десяти точкам, мкм;

d – диаметр сверла 12 мм; S – подача (0,06; 0,08; 0,1; 0,12 мм/об);

V – скорость резания (12; 14; 16 м/мин).

Решение задачи:

Поставленную задачу можно решить методом по координатного

спуска.

Известны: диаметр сверла d = 12 мм; уровни варьирования по-

дачей S = 0,06, 0,08, 0,10, 0,12 мм/об и скоростью резания

V = 12, 14, 16 м/мин. Зафиксируем один из варьируемых параметров (примем V = 12 м/мин) и найдем минимум значения параметра Rz при варьировании V в заданном диапазоне. Используя зависимость (32), получим:

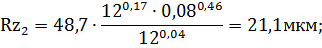
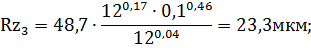
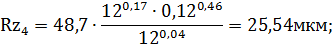
Как видим, минимальное значение Rz обеспечивается при

S = 0,06 мм/об и равно 18,5 мкм.

Зафиксируем теперь параметр S_min = 0,06 мм/об и найдем минимум выходного параметра Rz при изменении V в заданном диапазоне по зависимости (32):

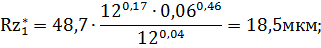
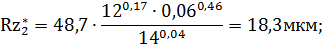
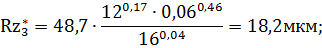
Минимальное значение Rz обеспечивается при V = 16 м/мин и

равно 18,2 мкм. Следовательно, искомое минимальное значение Rz

при сверлении отверстия обеспечивается при S = 0,06 мм/об и

V = 16 м/мин и равно 18,2 мкм.

Для решения поставленной задачи потребовалось семь шагов

приближения к искомому решению. Число шагов приближения к искомому решению можно определить по формуле:

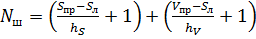, (33)

где Sл, Sпр − соответственно левая и правая границы диапазона изменения подачи S;

ℎ_S − шаг (уровень) изменения подачи S;

Vпр, Vл − соответственно левая и правая границы диапазона изменения скорости резания V;

ℎ_V − шаг (уровень) изменения скорости резания V:

,

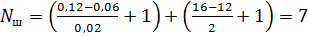Таким образом, на значение числа шагов Nш приближения к искомому решению влияют число, диапазоны и уровень изменения варьируемых параметров. Увеличение диапазона и числа варьируемых параметров при уменьшении уровня их изменения приведет к увеличению Nш, а, следовательно, к росту времени, затрачиваемого на проведение эксперимента. Если воспользоваться программой решения задачи на ЭВМ, то можно существенно сократить затраты времени на ее решение (рис. 5).

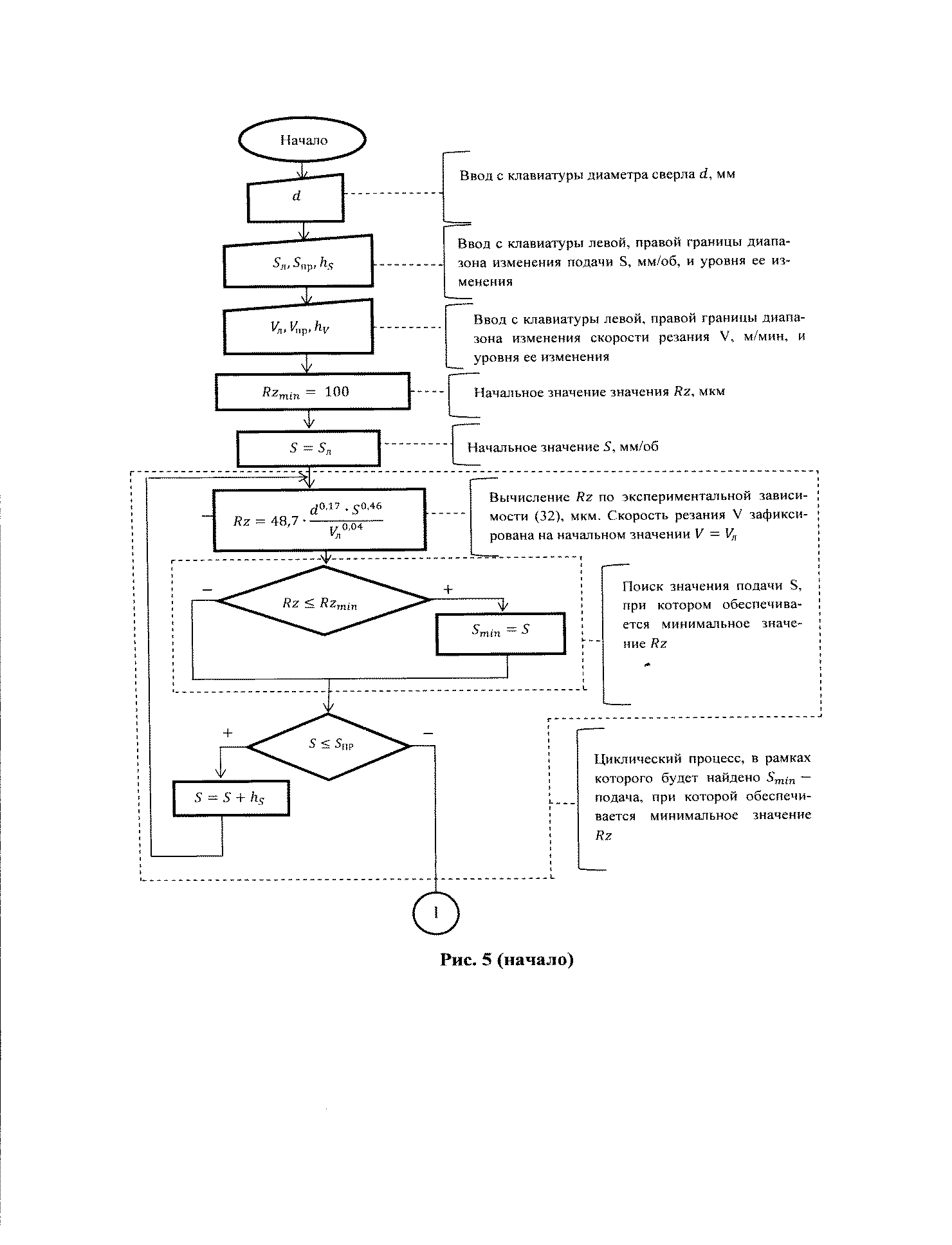
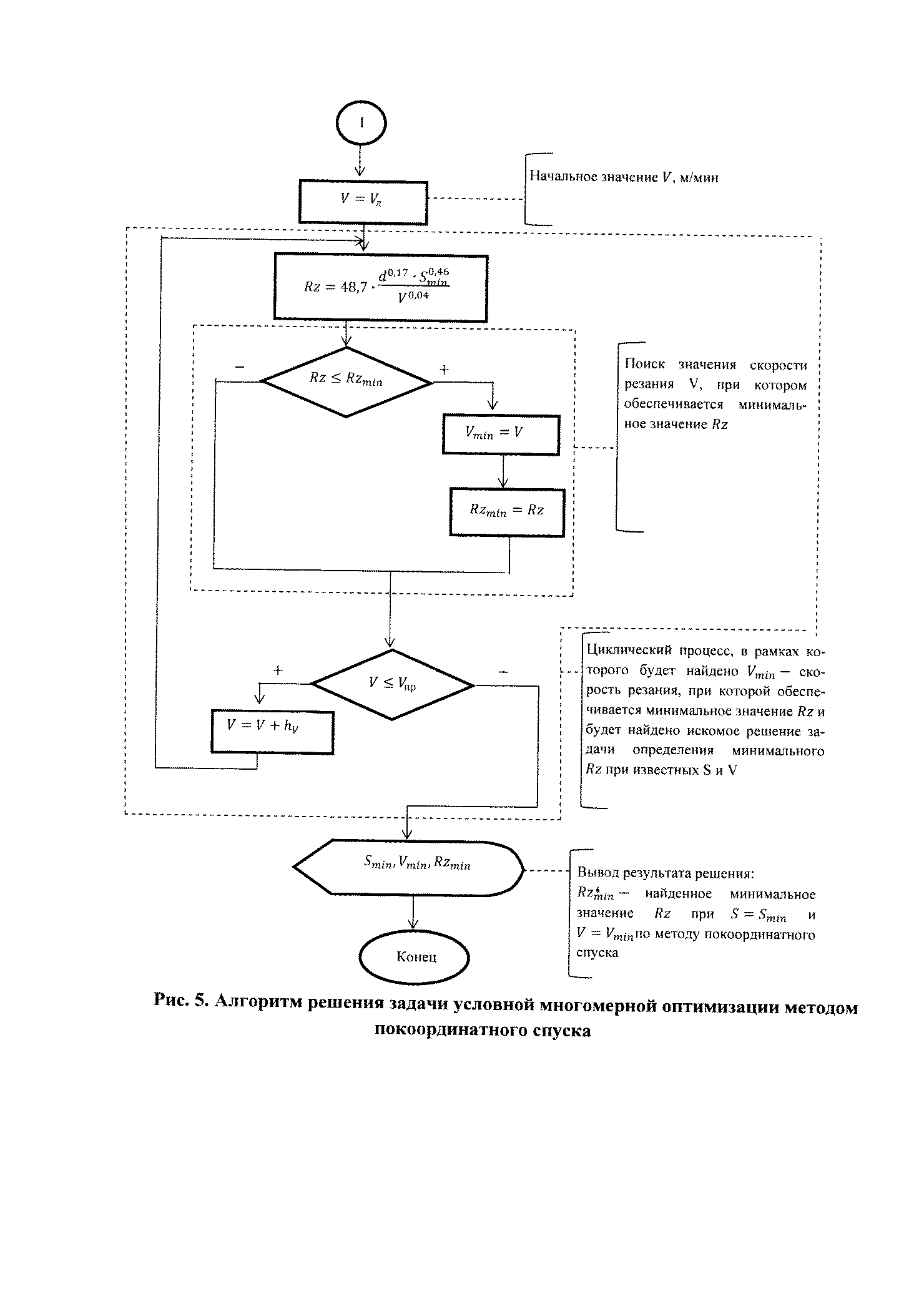
В рассмотренном примере реализована методика поиска оптимального значения целевой функции, предпринятая для решения задачи условной двухмерной оптимизации на основе метода покоординатного спуска. Эту методику можно реализовать для решения других аналогичных задач.