ЭНЕРГИЯ, ЗАТРАЧЕННАЯ НА ПЕРЕМЕЩЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ

Рассмотрим свободную частицу с положительным зарядом Q в равномерном электрическом поле (рис.1.2. )

вставить рис. 1.5(Евдокимов, стр 16)

Рис.1.2

Эта частица будет перемещаться по направлению действующей на нее силы F_э . При перемещении частицы на пути l между точками 1 и 2 за­трачивается энергия (совершается работа):

W₁,₂ =A_1,2= F_эl.

Учитывая формулу (1.2), выразим энергию через напряжен­ность электрического поля Е:

с. W₁,₂ =A_1,2=EQl.

Работа при перемещении заряженной частицы совершается в результате силового взаимодействия частицы с внешним полем. Численно она пропорциональна напряженности поля и величине заряда.

Работа считается положительной, если заряженная частица перемещается по направлению сил поля, и отрицательной, если перемещение вызывается действием посторонних сил против направления сил электрического поля.

Аналогичные выводы можно сделать и для неравномерного поля, определяя работу при перемещении заряженной частицы между точками 1 и 2 как сумму элементарных значений работы dA , совершаемой на каждом бесконечно малом отрезке пути dl , в пределах которого напряженность поля можно считать постоянной:

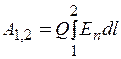(1.3)

где Е_п — проекция вектора напряженности поля на направление движения заряженной частицы.

Общая величина работы А на замкнутом пути 1-4-2-5-1 равна нулю:

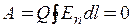(1.4)

Отсюда следует, что работа, совершаемая силами поля при перемещении заряженной частицы между двумя точками, не зависит от выбранного пути, а определяется положением начальной и конеч­ной точек пути (1 и 2), т. е. расстоянием l.

Электрическое напряжение. Потенциал

Количество работы зависит не только от величин, относящихся к полю E,l , но и от заряда частицы Q . Поэтому с энергетической точки зрения поле вдоль рассматриваемого пути характеризуется работой, приходящейся на единицу заряда: .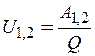

Это отношение называется электрическим напряжением.

Электрическое напряжение есть энергетическая характеристи­ка поля вдоль рассматриваемого пути из одной точки в другую, которой оценивается возможность совершения работы при перемещении заряженных частиц между этими точками.

Нетрудно найти связь напряженности равномерного поля с напряжением между двумя любыми точками:

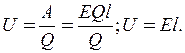(1.5 )

Единица электрического напряжения

[U] = [A/Q]=Джоуль/кулон = вольт(В)

Применяются также производные от вольта:

1 киловольт (кВ) = 10³ В;

1 милливольт (мВ)=10 ^-3 В;

1 микровольт (мкВ)=10 ^-6 В.

Учитывая, что работа, совершаемая при перемещении заряженной частицы в электрическом поле, зависит от положе­ния начальной и конечной точек пути, для расчета можно ввести энергетическую характеристику поля в каждой точке, величина которой является функцией положения точки. Такой характеристикой является электрический потенциал.

Предположим, что пробная частица, обладающая зарядом Q , расположена в точке 1 электрического поля (см. рис. 1.2) и, следовательно, находится под действием силы F_э . Элект­рическое поле действует на эту частицу подобно тому, как действует на тело поле тяготения, т. е. частица обладает потенциальной энергией A₁ .

При перемещении заряженной частицы из точки 1 в точку 2 совершается работа A ₁,₂, связанная с действием той же силы F_э . Работу A ₁,₂ нужно рассматривать как убыль потен­циальной энергии заряженной частицы при перемещении ее между указанными точками.

Следовательно, потенциальная энергия в точке 2

W₂ =W₁-W_1,2

Электрическим потенциалом поля называется отношение потенциальной энергии заряженной частицы, по­мещенной в данную точку электрического поля, к величине ее заряда в этой точке:

V₁=W₁/Q; V₂=W₂/Q.

Таким образом, напряжение между двумя точками элект­рического поля равно разности потенциалов поля в этих точках:

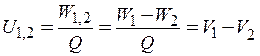(1.6)

Аналогичные рассуждения можно привести, рассматривая заряженную частицу в точках 2, 3 и др.

Потенциальная энергия заряженной частицы в электрическом поле уменьшается при переходе от точки к точке по направ­лению линий напряженности. Она становится равной нулю за пределами электрического поля, где сила F_э = 0.

При наличии электрического поля бесконечной протяжен­ности сила F_э равна нулю в бесконечности.

При обратном перемещении заряженной частицы против силы взаимодействия ее с электрическим полем потенциальная энергия будет возрастать за счет работы внешней неэлектрической силы.

Потенциальную энергию можно определить относительно какого-либо уровня, принятого за начальный. При теоретичес­ких исследованиях за начальный потенциал принимают потен­циал бесконечно удаленной точки поля, где он равен нулю.

Таким образом, потенциал любой точки электрического поля характеризуется энергией, которая затрачивается (или может быть затрачена) на перемещение, единицы заряда из данной точки электрического поля в бесконечность (или наоборот).

При решении практических задач, относящихся к электричес­ким установкам, обычно полагают начальным потенциал земли, который принимают равным нулю.

Проводники в электрическом поле

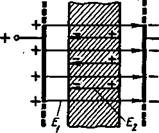
Рис.1.3.

В металлическом теле (рис. 1.3) под действием внешнего электрического поля с напряженностью E₁ свободные элект­роны перемещаются к одной поверхности, которая получает отрицательный заряд. Противоположная поверхность получает положительный заряд.

Явление смещения свободных заряженных частиц на повер­хность проводника, помещенного в электрическом поле, называ­ется электростатической индукцией.

В результате разделения зарядов в проводнике создается внутреннее электрическое поле с напряженностью Е₂, направ­ленное противоположно внешнему. Движение свободных эле­ктронов в проводнике при электростатической индукции суще­ствует кратковременно, но продолжается до тех пор, пока напряженности внешнего и внутреннего полей не станут равными.

При равенстве Е₁ = Е₂ разделение зарядов в проводнике прекращается, так как результирующая напряженность элект­рического поля равна нулю.

Благодаря наличию в проводнике свободных заряжен­ных частиц электростатическое поле в нем существовать не может.

Напряжение между двумя любыми точками проводника равно нулю, следовательно, потенциал его во всех точках один и тот же. Таким образом, проводник представляет собой эквипотенциальный объем, а его поверхность является эк­випотенциальной поверхностью результирующего электричес­кого поля.

Если в электрическое поле поместить проводник с полостью внутри, то и в этом случае заряженные частицы будут только на поверхности. Внутри металла и полости электрическое поле отсутствует.

Это свойство проводников используется для электростати­ческого экранирования, т. е. для защиты какого-либо устрой­ства от действия внешнего электрического поля (защищаемый объект помещается в металлическую коробку или сетку с малыми отверстиями).

Электрическая емкость

При анализе электростатической системы, состоящей из электропроводного заряженного тела и его электрического поля, определяют характеристики поля (напряженность, потен­циал). Их можно определить в каждой точке пространства, где есть электрическое поле. Характеристиками заряженного тела в этой системе являются его электрический заряд Q и потенциал V , причем эти величины характеризуют тело не в отдельных точках, а в целом и связаны между собой. В вакууме связь заряда и потенциала в этом случае выражается пропорциональной зависимостью Q=CV, где коэффициентом пропорциональности является величина С, называемая электрической ем­костью тела:

C=Q/V

Таким образом, электрическая емкость заряженного тела ха­рактеризуется величиной заряда, который нужно сообщить этому телу для того, чтобы его потенциал изменился на единицу.

Наибольшее значение имеют системы из двух электрически изолированных между собой электропроводных тел, которые получают равные по величине, но противоположные по знаку заряды. Электрическую емкость подобных систем приходится определять и учитывать при проектировании и расчетах электро­технических и радиотехнических устройств и установок. В элект­ротехнике и радиотехнике широко применяют специальные устройства, которые называют электрическими конденсато­рами.